Применения определенных интегралов.
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
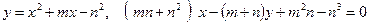 ;
;
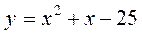
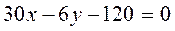
Или
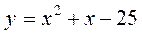
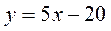
Построим графики линий и найдем точки пересечения:
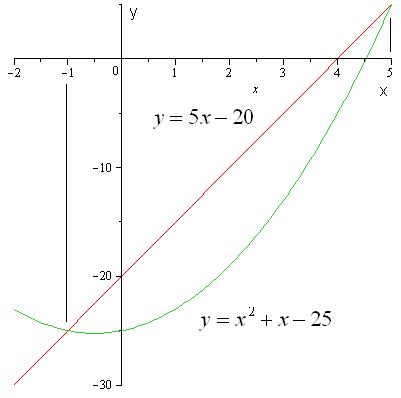
Тогда площадь фигуры вычислится по формуле
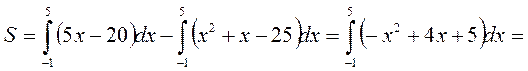
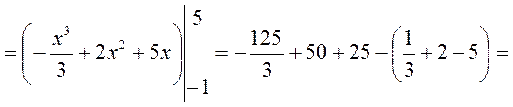
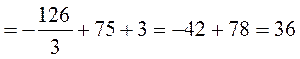
Дополнительные примеры
Вар 1. а) 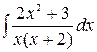 , б)
, б) 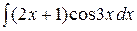 , в)
, в) 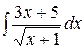 , г)
, г) 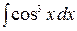 ;
;
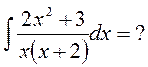
Сначала из неправильной дроби сделаем правильную:
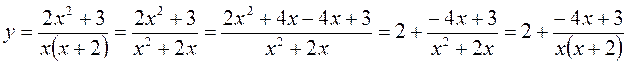
Возьмем производную от знаменателя:
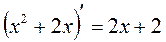 . Заметим, что
. Заметим, что 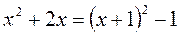
Окончательно преобразуем у:
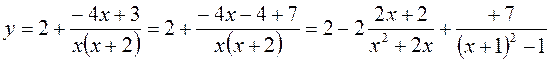
Тогда наш интеграл будет таким:
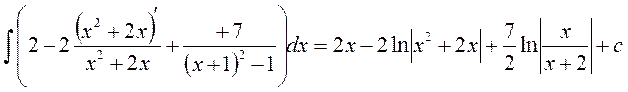
Однотипные логарифмы можно привести и тогда получим:
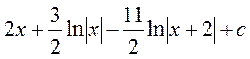 Это ответ.
Это ответ.
Замечание. Можно было разложить выражение на простейшие
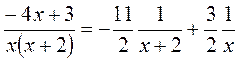
И сразу получить окончательный ответ.
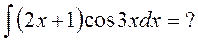
Такой интеграл часто встречается, поэтому удобней решить его в общем виде:
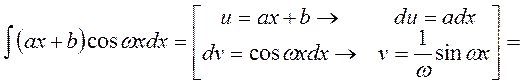
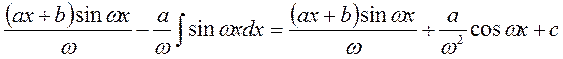
Тогда наш интеграл будет таким:
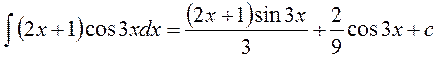
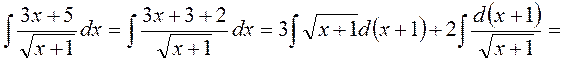
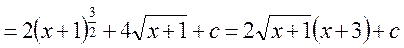
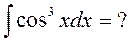
Преобразуем:
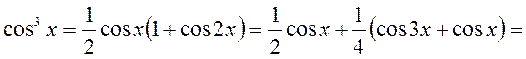
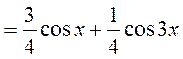
Тогда наш интеграл будет равен
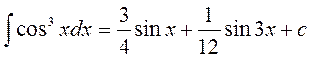
Вариант 1
1. Упростить выражение Ø
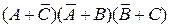
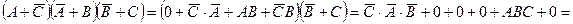
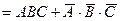
2. Три стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятности попадания у стрелков соответственно равны 0,7; 0,6 и 0,9. Найти вероятность того, что попадет третий стрелок, а первый и второй промахнутся.
P(попадет третий стрелок, а первый и второй промахнутся)=
=0,9*0,3*0,4=0,108
3. Из артиллерийской установки произведено 5 выстрелов. Вероятность попадания при одном выстреле равна 0,8. Определить:
· вероятность получить не менее одного попадания;
P(получить не менее одного попадания)=
1-P(ноль попаданий)=1-0,25 =1-0,00032=0,99968
· наиболее вероятное число попаданий.
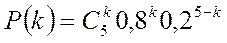
| k |
| F(x) | |
| 0,00032 | 0,00032 | ||
| 0,0064 | 0,00672 | ||
| 0,0512 | 0,05792 | ||
| 0,2048 | 0,26272 | ||
| 0,4096 | 0,67232 | ||
| 0,32768 |
4 - наиболее вероятное число попаданий. И математическое ожидание также равно np=4.
4. Дан ряд распределения случайной величины Х.
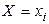 | -2 | |||
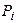 | 0,2 | 0,15 | 0,3 | 0,35 |
Найти:
· интегральную функцию распределения;
Найдем интегральную функцию распределения по ряду:
| X | Pk | F(x) |
| -2 | 0,2 | 0,2 |
| 0,15 | 0,35 | |
| 0,3 | 0,65 | |
| 0,35 |
· вероятность неравенства 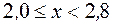 ;
;
P( 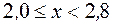 )=0 из ряда распределения.
)=0 из ряда распределения.
· 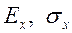 .
.
Еx (в книгах обозначается Мх)= 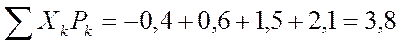
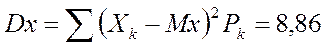
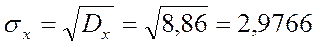
Эти вычисления иллюстрируются таблицей:
| X | Pk | F(x) | X*pk | Pk*(X-Mx)^2 |
| -2 | 0,2 | 0,2 | -0,4 | 6,728 |
| 0,15 | 0,35 | 0,6 | 0,006 | |
| 0,3 | 0,65 | 1,5 | 0,432 | |
| 0,35 | 2,1 | 1,694 | ||
| Summ= | 3,8 | 8,86 |
Построить многоугольник распределения и график функции F(x).
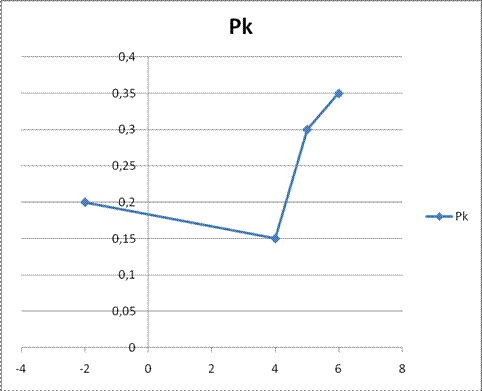
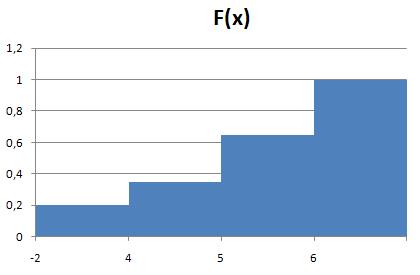
5. Дана интегральная функция распределения
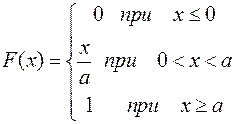
Определить f(x). Найти вероятность попадания случайной величины Х на отрезок 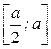 и математическое ожидание.
и математическое ожидание.
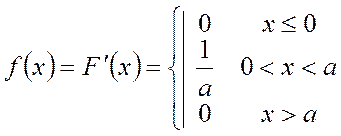
Отдельное задание по теории вероятностей:
Из колоды в 36 карт потеряли 3. После этого из оставшихся 33 карт вытащили 4. Какова вероятность того, что эти 4 карты представляют разные масти?
Решение.
A=4 карты представляют разные масти.
H1= потеряли 3 карты и все разных мастей. P(H1)=(27/35)*(18/34)
H2= потеряли 3 карты: 2 одной масти, а 1 другой. P(H2)=3*(8/35)*(27/34)
H3= потеряли 3 карты и все одной масти. P(H3)= (8/35)*(7/34)
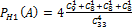
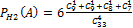
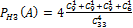
Далее по формуле полной вероятности.
P(A)= )=(27/35)*(18/34)*PH1(A)+ 3*(8/35)*(27/34)* PH2(A)+ (8/35)*(7/34)* PH3(A)=
В урне 6 красных и 4 зеленых шара. Какова вероятность того,что два наугад выбранных шара будут разного цвета?
A= два наугад выбранных шара будут разного цвета.
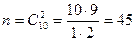
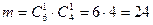
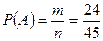
1. Вероятность того, что студент сдаст экзамен, равна 0.4 независимо от дня сдачи. Студент делает не более трех последовательных попыток сдать экзамен(следующая попытка предпринимается при неуспехе предыдущей ) .Какова вероятность того ,что студент сдаст экзамен?
А= студент сдал экзамен.
A1= студент сдал экзамен с первой попытки.
A2= студент сдал экзамен со второй попытки.
A3= студент сдал экзамен с третьей попытки.
Очевидно, что 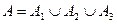 . Так как события А1, А2 и А3 несовместны, то
. Так как события А1, А2 и А3 несовместны, то 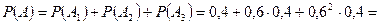 сама сосчитай.
сама сосчитай.
2. Три студента (Иванов, Петров, и Семенов) сдают экзамен по теории вероятностей. Вероятность того, что Иванов сдаст экзамен, равна 0.6 , Петров-0.5 ,Семенов-0.4 Двое студентов сдали экзамен ,а один не сдал. Что вероятнее: сдал Семенов или не сдал?
А= Двое студентов сдали экзамен ,а один несдал.
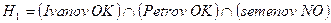
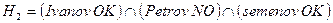
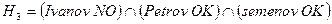
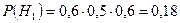
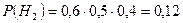
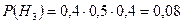 Очевидно, что
Очевидно, что 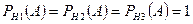 . По формуле полной вероятности находим
. По формуле полной вероятности находим 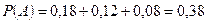 . Уточним первую гипотезу по формуле Бэйеса:
. Уточним первую гипотезу по формуле Бэйеса: 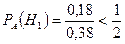 . По первой гипотезе Семенов не сдал экзамен (при остальных сдал). Вероятность этой гипотезы при наступлении события А меньше половины. Следовательно, вероятнее, что Семенов сдал.
. По первой гипотезе Семенов не сдал экзамен (при остальных сдал). Вероятность этой гипотезы при наступлении события А меньше половины. Следовательно, вероятнее, что Семенов сдал.
3. При въезде в новое помещение в осветительную сеть было включено 5 электроламп. Каждая лампа в течение года перегревает с вероятностью 0.6 Определить вероятность того, что количество перегоревших за год ламп будет не менее двух и не более трех. Для DCB –количество перегоревших в течение года ламп построить ряд распределения и график ФР.
Данная ДСВ, очевидно имеет биномиальное распределение и вероятности считаются по формуле 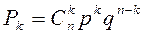 . В нашем случае p=0,6 q=1-p=0,4 n=5. Имеем ряд распределения:
. В нашем случае p=0,6 q=1-p=0,4 n=5. Имеем ряд распределения:
| X | Pk | F(x) |
| 0,01024 | 0,01024 | |
| 0,0768 | 0,08704 | |
| 0,2304 | 0,31744 | |
| 0,3456 | 0,66304 | |
| 0,2592 | 0,92224 | |
| 0,07776 |
Построим график функции распределения:
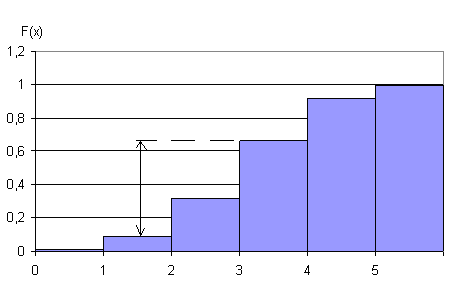
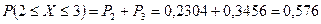
4. Задана HCB: F(x)=B+A arctg(x) Найти A, B, p(x) проверить ,имеется и у этой HCB MO определить верояность P(-1<X<1). Построить график ФР и ПР. Показать на каждом из графиков найденную вероятность.
Так как 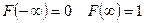 , то
, то 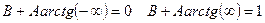 или
или 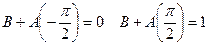 , откуда
, откуда 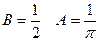 . Так как
. Так как 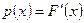 , то, дифференцируя, имеемРаспределение Коши.
, то, дифференцируя, имеемРаспределение Коши.
Плотность распределения:
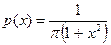
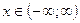
Функция распределения:
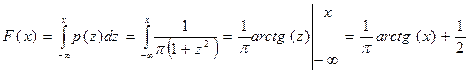
Математическое ожидание в обычном смысле не существует, так как несобственный интеграл
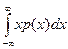 в данном случае расходится. Действительно,
в данном случае расходится. Действительно, 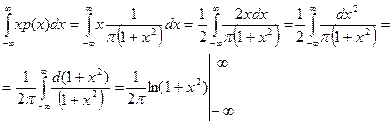
Очевидно, что такой интеграл расходится.
Но в СМЫСЛЕ ГЛАВНОГО ЗНАЧЕНИЯ математическое ожидание существует и равно нулю. Действительно:
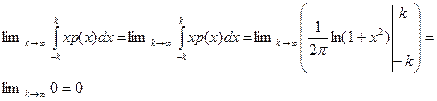
Дисперсия распределения Коши не существует (бесконечна). Если интеграл 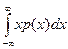 расходится, то интеграл
расходится, то интеграл 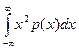 и подавно расходится.
и подавно расходится.
Вероятность попадания в интервал для распределения Коши вычисляется обычным образом. Например,
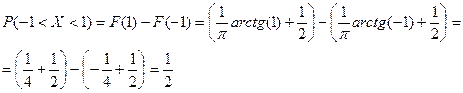
В условиях задачи 6 найти ПР(y) CB 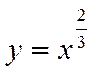
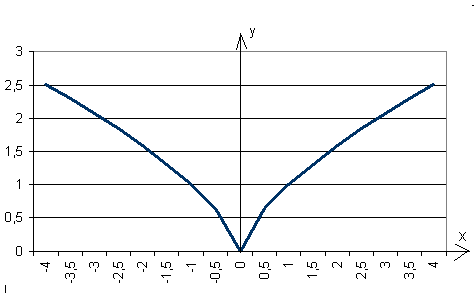
Определим области по y, различающиеся количеством обратных функций:
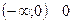
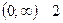
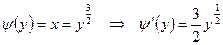 . Подставим в формулу Смирнова:
. Подставим в формулу Смирнова: 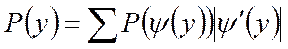
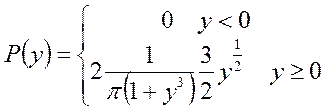 или
или 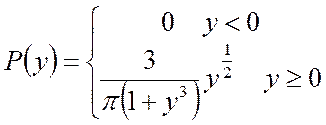
11. Пятьчеловек садятся на пять стульев случайным образом, несмотря на то, что места для них были определены, но эти сведения не успели им передать к моменту занятия мест. Найти вероятность того, что никто из них не сел на предназначенное ему место.
Решение.
Эксперимент состоит в выборе пяти человек пяти мест. Очевидно, что общее число равновозможных исходов эксперимента равно 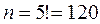 . Число mисходов, соответствующее наступлению интересующего нас события (благоприятных исходов) в данном случае обозначим
. Число mисходов, соответствующее наступлению интересующего нас события (благоприятных исходов) в данном случае обозначим 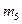 . Обозначим
. Обозначим 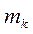 - число благоприятных исходов в аналогичной задаче, где kчеловек выбирают каждый себе место из kмест. Обозначим
- число благоприятных исходов в аналогичной задаче, где kчеловек выбирают каждый себе место из kмест. Обозначим 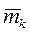 - число неблагоприятных исходов. Очевидно, что
- число неблагоприятных исходов. Очевидно, что 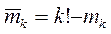 . Легко видеть, что
. Легко видеть, что 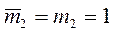 . Действительно, два человека либо сидят на своих местах, либо оба не на своих. Непосредственной проверкой нетрудно убедиться, что
. Действительно, два человека либо сидят на своих местах, либо оба не на своих. Непосредственной проверкой нетрудно убедиться, что 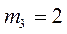 ,
, 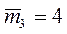 . Подсчитаем теперь количество неблагоприятных исходов
. Подсчитаем теперь количество неблагоприятных исходов 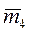 . Четверо человек могут сесть каждый на свое место (один исход). Возможно, что двое сидят на своих местах, а остальные не на своих (
. Четверо человек могут сесть каждый на свое место (один исход). Возможно, что двое сидят на своих местах, а остальные не на своих ( 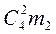 исходов) Также возможно, что один человек сидит на своем месте, а трое не на своих (
исходов) Также возможно, что один человек сидит на своем месте, а трое не на своих ( 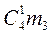 исходов). В результате имеем
исходов). В результате имеем 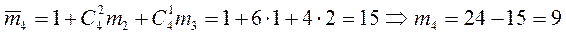 . Проводя аналогичные рассуждения, получим
. Проводя аналогичные рассуждения, получим 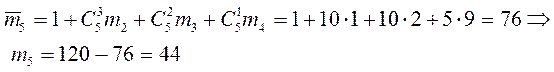
Ответ 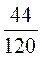 .
.
