Расчет электрической цепи частотным методом при несинусоидальном воздействии

Расчет линейной электрической цепи при периодическом несинусоидальном воздействии на основании принципа суперпозиции проводится для каждой составляющей воздействия (после разложения его в ряд Фурье) отдельно, так, как если бы в цепи действовала только эта составляющая. Расчет цепи для постоянной составляющей проводится так же, как в случае, когда к цепи подключен источник постоянного напряжения.

При расчете цепи для отдельных гармонических составляющих следует пользоваться символическим методом (методом комплексных амплитуд). Для k-й гармоники комплексное сопротивление ветви, содержащей последовательно соединенные элементы R, L и C, Z^(k) = R + jkw₁L – j/(kw₁C), где w₁ = 2p / T = 2p f _ G0AB>B0 >A=>2=>9 (?5@2>9) 30@<>=8:8, k — номер гармоники (k = 1, 2, 3, ...).

Выбранный метод расчета цепи (по законам Кирхгофа, контурных токов и т.д.) для одной гармонической составляющей не зависит от метода расчета той же цепи для другой гармоники. Из выражения для комплексной передаточной функции W( jw) = Y( jw) / X( jw) = Y_m( jw) / X_m( jw), >?@545;O5<>9 :0: >B=>H5=85 комплексных амплитуд (комплексных действующих значений) электрических величин на выходе и входе цепи в заданном режиме работы, следует, что при заданном гармоническом воздействии
u_вх = U_mвхsin(wt +y_u) 2KE>4=>5 =0?@O65=85 <>6=> >?@545;8BL A;едующим образом:

U_mвых = W( jw)U_mвх = W(w )U_mвхexp[ j(y_uвх + j)].

Так как периодическое несинусоидальное воздействие имеет дискретный спектр с частотами kw₁, B> ?@8 459AB288 =0 2E>4 F5?8 k-й гармоники появится реакция с частотой kw₁, 0<?;8BC4>9

U_mвых = W(kw₁)U_mвх и начальной фазой y_uвых = [y_uвх + j(kw₁)]. _45AL W(kw₁) _ <>4C;L, j(kw₁) _ 0@3C<5=B :>MDD8F85=B0 ?5@едачи по напряжению цепи на частоте kw₁.

Суммируя все выражения для мгновенных значений гармоник, включая постоянную составляющую выходного напряжения, согласно принципу суперпозиции будем иметь выражение для выходного напряжения.

Пример 11. Для схемы четырехполюсника (см. рис. 2) рассчитать u_вых(t) при входном воздействии u₁(t) в виде разнополярных прямоугольных импульсов (рис. 17), ряд Фурье которого содержит только синусоидальные составляющие нечетных гармоник (k = 1, 3, 5, ...): u₁(t) = = .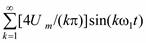

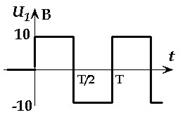
Рис. 17

Решение. Будем считать АЧХ и ФЧХ заданного четырехполюсника
известными (см. пример 5): W(w) = 1 / / [(1 – w²LC)² + (wRC)²]^1/2, j(w) = -jarctg[wRC/(1 – w²LC)].

На рис. 13 показаны графики этих характеристик.

Заменим в АЧХ и ФЧХ текущую частоту w =0 48A:@5B=CN kw₁:

W(kw₁) = 1/[(1 _ k²w₁²LC)² + (kw₁RC)²]^1/2, j(kw₁) = - jarctg[kw₁RC/(1 – k²w₁²LC)].

Выходное напряжение в общем виде может быть записано следующим образом:

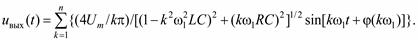
Нетрудно заметить, что четырехполюсник осуществляет изменение спектра входного напряжения. Вследствие этого выходное напряжение отличается по форме от входного воздействия.

Список рекомендуемой ЛИТЕРАТУРЫ

1. Попов В.П. Основы теории цепей. М.: Высш. шк., 1985. 496 с.

2. Нейман Л.Р. Демирчан К.С. Теоретические основы электротехники: В 2 т. Т. 1. Л.: Энергоиздат, 1981. 533 с.

3. Атабеков Г.И. Основы теории цепей. М.: Энергия, 1969. 424 с.

4. Лосев А.К. Теория линейных электрических цепей. М.: Высш. шк., 1987. 512 с.

5. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. М.: Высш. шк., 1996. 638 с.

6. Шебес М.Р. Задачник по теории линейных электрических цепей. М.: Высш. шк., 1990. 544 с.

7. Гладилина Г.А., Маланьин В.А. Частотные методы анализа электрических цепей. М:. Изд-во МГТУ им. Н.Э. Баумана, 1996. 44 с.

8. Аболымов Ю.В., Гладилина Г.А. Расчет электрических цепей методами частотного анализа. М.: Изд-во МГТУ им. Н.Э. Баумана, 1991. 80 с.

9. Масленникова С.И., Аболымов Ю.В. Анализ электромагнитных процессов в электрических цепях во временной области. М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. 40 с.

10. Стрелков Б.В., Масленникова С.И. Методы анализа линейных электрических цепей. М.: Изд-во МГТУ им. Н.Э. Баумана, 1991. 43 с.

11. Плаксин И.И., Смирнов А.В. Методы анализа разветвленных электрических цепей. М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. 28 с.

12. Гладилина Г.А. Сборник задач по ТОЭ для проведения семинаров и рубежного контроля. М.: Изд-во МГТУ им. Н.Э. Баумана, 1995. 74 с.

13. Маланьин В.А., Шерстняков Ю.Г. Анализ установившихся и переходных процессов в линейных электрических цепях. М.: Изд-во МГТУ им. Н.Э. Баумана, 1991. 48 с.

14. Николаев С.С., Шерстняков Ю.Г. Анализ установившихся режимов в четырехполюсниках и длинных линиях. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 48 с.

15. Грибова С.Н. Электрические цепи с операционными усилителями. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 36 с.

16. Масленникова С.И., Болотнов С.А. Резонансные явления в электрических цепях. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 24 с.