Модифицированный метод Эйлера с пересчетом

Численное решение обыкновенных дифференциальных уравнений

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:

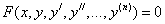, где x – независимая переменная, 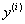- i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных 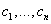, т.е. общее решение имеет вид .

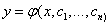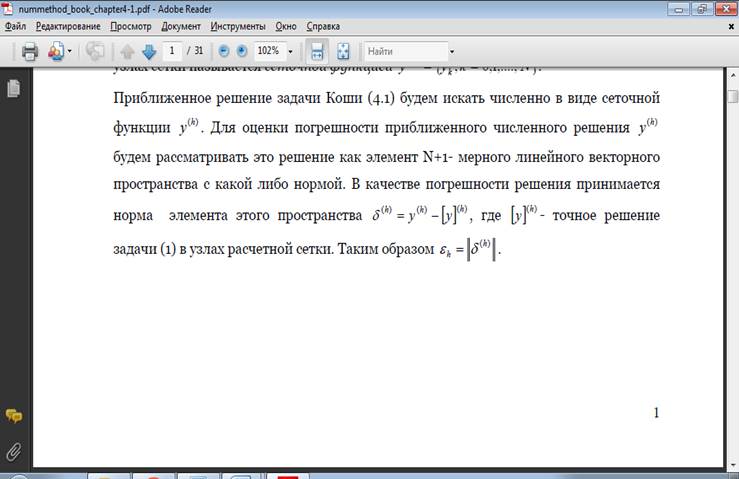
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Задача Коши

Решение задачи Коши

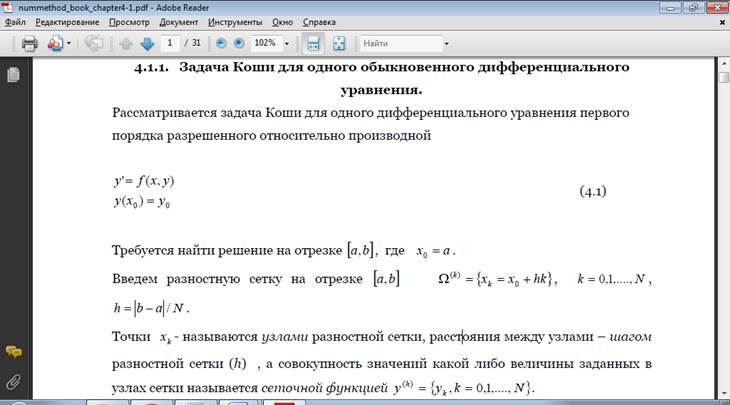
Задача Коши для одного обыкновенного дифференциального уравнения.

Метод Эйлера

Описание метода

Пусть дана задача Коши для уравнения первого порядка

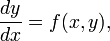
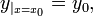
где функция 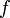определена на некоторой области 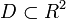. Решение разыскивается на интервале 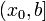. На этом интервале введем узлы

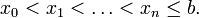
Приближенное решение в узлах 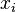, которое обозначим через 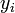определяется по формуле

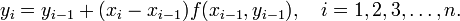
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности

Метод Эйлера является методом первого порядка. Если функция 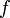непрерывна в 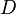и непрерывно дифференцируема по переменной 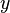в 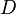, то имеет место следующая оценка погрешности

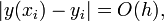
где 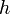— средний шаг, то есть существует 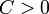такая, что .

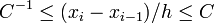Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

.

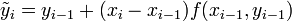Коррекция:

.

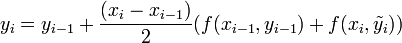Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидностьметодов Рунге-Кутты (предиктор-корректор).