Фрагмент матрицы определения параметров математических

функций при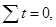

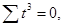
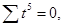
Год	Условные обозначения		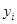		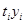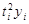t³y	lg y	t·lgy
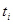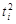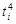			tі³	ti^6
	-2						-60			1,47	-2,94
	-1						-32			1,50	-1,5
										1,51
										1,50	1,5
										1,50
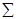										7,48	0,06

Далее найдем расчетные и вспомогательные данные для определения параметров моделей. Просчитываем несколько моделей, после чего выберем адекватную:

1. Для прямолинейной функции

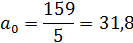
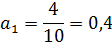
Таким образом, получаем:

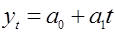= 31,8 + 0,4t.

ŷ_i - y_i (ŷ_i - y_i )²

ŷ_{1 =} 31,1 + 0,4*(-2) = 31 ŷ₁ – y₀ = 31 – 30 = 1 (ŷ₁ - y₀ )² = 1

ŷ_{2 =} 31,1 + 0,4*(-1) = 31,4 ŷ₂ – y₀ = 31,4 – 32 = -0,6 (ŷ₂ - y₁ )² = 0,36

ŷ_{3 =} 31,1 + 0,4*0 = 31,8 ŷ₃ – y₀ = 31,8 – 33 = -1,2 (ŷ₃ - y₂ )² = 1,44

ŷ_{4 =} 31,1 + 0,4*1 = 32,2 ŷ₄ – y₀ = 32,2 – 32 = 0,2 (ŷ₄ - y₃)² = 0,04

ŷ_{5 =} 31,1 + 0,4*2 = 32,6 ŷ₅ – y0 = 32,6 – 32 = 0,6 (ŷ₅ - y₄)² = 0.36

2. Для параболы второго порядка

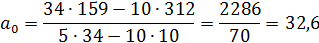
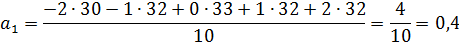
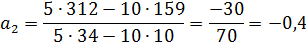
Таким образом, получаем:

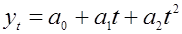= 32,6+0,4t+(-0,4)t²

ŷ_i - y_i (ŷ_i - y_i )²

ŷ_{1 =} 32,6+ 0,4*(-2)+ (-0,4)*4= 61,4 ŷ₁ – y₀ = 31,4 (ŷ₁ - y₀ )² = 986

ŷ_{2 =} 32,6 + 0,4*(-1)+(-0,4)*1= 64,6 ŷ₂ – y₀ = 32,6 (ŷ₂ - y₁ )² = 1063

ŷ_{3 =} 32,6+ 0,4*0+ (-0,4)*0= 67 ŷ₃ – y₀ = 34 (ŷ₃ - y₂ )² = 1156

ŷ_{4 =} 32,6+ 0,4*1+(-0,4)*1=68,6 ŷ₄ – y₀ = 36,6 (ŷ₄ - y₃)² = 1339

ŷ_{5 =} 32,6 + 0,4*2+(-0,4)*= 69,4 ŷ₅ – y0 = 37,4 (ŷ₅ - y₄)² = 1399

_{3. Для параболы третьего порядка}

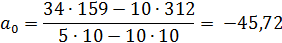
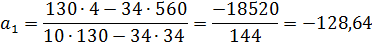
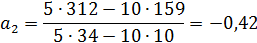
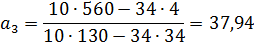
Таким образом, получаем:

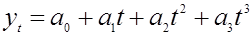= (-45,72)+(-128,64)t+(-0,42)t²+37,94t³

ŷ_i - y_i (ŷ_i - y_i )²

ŷ_{1 =} 513,34 ŷ₁ – y₀ = 483,34 (ŷ₁ - y₀ )² = 233617,556

ŷ_{2 =} 120,41 ŷ₂ – y₀ = 88,41 (ŷ₂ - y₁ )² = 7816,328

ŷ_{3 =} -45,72 ŷ₃ – y₀ = -78,72 (ŷ₃ - y₂ )² = 6196,328

ŷ_{4 =} -136,8 ŷ₄ – y₀ = -168,8 (ŷ₄ - y₃)² = 28493,44

ŷ_{5 =} -1,1 ŷ₅ – y0 = -33,1 (ŷ₅ - y₄)² = 1095,61

4. Для показательной функции

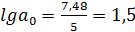
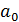= lg 1,5= 0,17

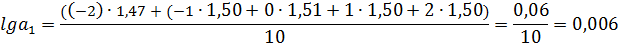
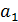= lg0,006= -2,22

Таким образом, получаем:

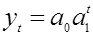= 0,17*(-2,22)^t

ŷ_i - y_i (ŷ_i - y_i )²

ŷ_{1 =} 0,03449 ŷ₁ – y₀ = -29,96 (ŷ₁ - y₀ )² = 897,60

ŷ_{2 =} -0,07658 ŷ₂ – y₀ = -32,07 (ŷ₂ - y₁ )² = 1028,48

ŷ_{3 =} 0,17 ŷ₃ – y₀ = -32,83 (ŷ₃ - y₂ )² = 1077,80

ŷ_{4 =} -0,3774 ŷ₄ – y₀ = -32,37 (ŷ₄ - y₃)² = 1047,81

ŷ_{5 =} 0,83783 ŷ₅ – y0 = - 31,16 (ŷ₅ - y₄)² = 970,94

Адекватность определяется по значению стандартизированной ошибки аппроксимации. Для расчета построим таблицу 4.

Таблица 4

Фрагмент матрицы определения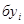

Год		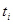	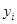Теоретические уровни по моделям
Прямолинейной функции	Функции параболы второго порядка	Функция параболы третьего порядка	Показательная функция
	-2			61,4	513,34	0,03449
	-1		31,4	64,6	120,41	-0,07658
			31,8		-45,72	0,17
			32,2	68,6	-136,8	-0,3774
			32,6	69,4	-1,1	0,83783
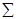					450,13	0,58834

Таблица 4.1

Год	ti	yi	Отклонения теоретических уровней 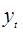от фактических уровней
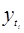Прямолинейной функции	Функции параболы второго порядка	Параболы третьего порядка	Показательной функции
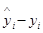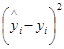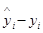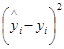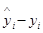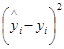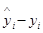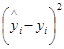	-2				31,4		483,34	233617,5	-29,96	897,6
	-1		-0,6	0,36	32,6		88,41	7816,3	-32,07	1028,5
			-1,2	1,44			-78,722	6196,8	-32,83	1077,9
			0,2	0,04	36,6		-168,8	28493,4	-32,37	1047,8
			0,6	0,36	37,4		-33,1	1095,6	-31,16	970,8
∑				3,2			291,13	277219,7	-158,39	5022,6

Построим график всех моделей

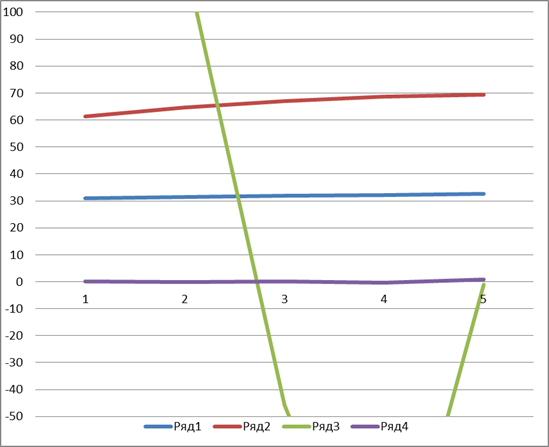
Ряд1 -Прямолинейная функция

Ряд2 - Функция параболы второго порядка

Ряд3 - Функция параболы третьего порядка

Ряд4 – Показательная функция

Определим адекватность по значению стандартизированной ошибки аппроксимации по формуле:

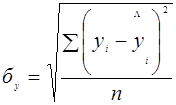(12)

где 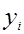- значение уровня i-го года (данные в задании),

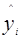, - значение уровня i-го года, полученное по математической модели;

1. Для прямолинейной функции:

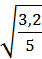= 0,8

2. Для параболы второго порядка:

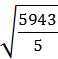= 34,4

3. Для параболы третьего порядка:

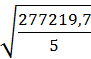= 7,4

4. Для показательной функции:

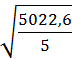= 31,6

Адекватной считается та модель, для которой 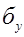минимальна. Такой в нашем случае является модель описания прямолинейной функцией 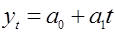= 31,8 + 0,4t.

Прогнозирование осуществляется по адекватной модели тренда. Подставляя в адекватную модель значение t = 5 (прогноз на 3 года), подсчитываем точечную оценку прогнозируемого параметра yt.

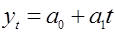= 31,8 + 0,4t = 31,8 + 0,4∙5 = 33,8, таким образом y_прог = 33,8.

Далее, с достоверностью 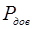= 0,95, определяем предельную возможную ошибку прогноза :

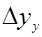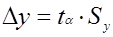, (13)

где 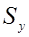- остаточное среднее квадратическое отклонение, определяется по формуле:

,

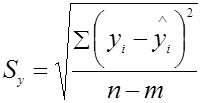(14)

где tα – коэффициент доверия, определяется по таблицам функции Стьюдента в зависимости от принятой достоверности .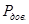

n – число уровней базисного ряда динамики,

m – число параметров адекватной модели тренда.

Тогда прогнозируемый параметр будет лежать в пределах

yt - Δy ≤ yпрог. ≤ yt+Δy.

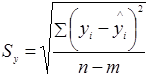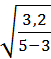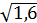= = = ± 1,26

Так как достоверная вероятность 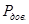= 0,95, то коэффициент доверия tα= 2. Предельно возможная ошибка прогноза

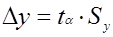= ± 1,26 ∙ 2 = ± 2,52

Заключение

Таким образом, развитие объекта по которому мы составили прогноз по адекватной модели тренда с установленной вероятностью, будет на уровне 33,8 млн. рублей. Однако, принимая во внимание возможную ошибку прогноза, необходимо учитывать, что доход от оказанных услуг будет в пределах от 31,8 млн. руб. до 36,32 млн. руб.

Библиографический список

Книги

Шмойлова Р.А., В.Г. Минашкин, Н.А. Садовникова, Е.Б. Шувалова Теория статистики - М: Финансы и статистика, 2007.

Статьи

Семчагов В.Н. "Экономическая безопасность: состояние банковской системы" // Вопросы экономики - 1996. - № 6.