Алгоритм поиска собственных векторов.

1. Вычислить определитель 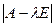и приравнять к нулю - получится характеристическое уравнение.

2. Решить характеристическое уравнение 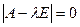, найти все собственные числа.

Их будет не больше, чем n, так как уравнение порядка n, так как по диагонали n элементов.

3. Подставить каждое конкретное 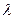в характеристическую матрицу, и решить однородную систему 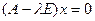. Таких шагов может быть n. Каждый раз надо изменить диагональ и заново решить систему!

ФСР системы это и будет собственный вектор для того .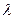

Пример. Найти собственные числа и векторы для .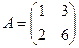

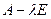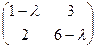= . Далее, 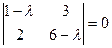. Тогда уравнение .

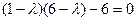Рещим это уравнение: 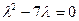. Получим .

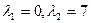Теперь подставим каждое 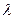и решим системы уравнений.

:

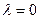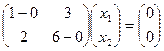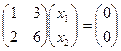, , система: 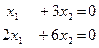. Общее решение: 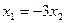, вектор .

:

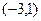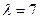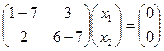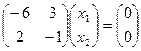, , система: 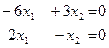. Общее решение: 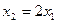, вектор .

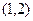Проверка:

, .

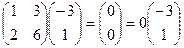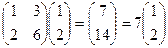Никакого третьего собственного числа в этом примере быть не может, так как матрица порядка 2, и характеристическое уравнение степени 2.

Теорема 5. Если базис состоит из собственных векторов, то матрица оператора в этом базисе диагональна.

Доказательство.

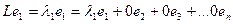, то есть 1-й столбец в матрице оператора это такие числа: .

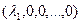Аналогично 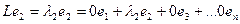, то есть 2-й столбец 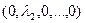. И т.д.

Таким образом, получится матрица оператора: .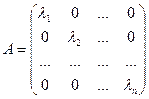

Теорема 6. Следующее свойство (Ax,y) = (x,Ay) выполняется 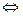матрица А симметрична (то есть ).

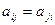Доказательство. Рассмотрим это равенство для базисных векторов: 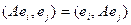. Если оно выполняется для любой пары базисных векторов, то есть для любых индексов i, j .

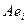, как показано раньше, это i-й столбец матрицы линейного оператора. Если скалярно умножить его на 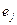, то есть на тот вектор, где все координаты 0 и только на месте j единица, - получим j - й элемент из i - го столбца, это 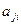в матрице.

Аналогично, 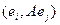это i - й элемент из j - го столбца, то есть .

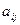Таким образом, 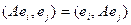эквивалентно тому, что 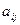= 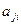для всех индексов i, j.

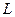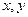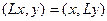Определение. Если для линейного оператора , для любой пары векторов верно , то 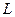называется симметрическим оператором.

Лекция № 6. 07. 10. 2016

Теорема 7. Собственные векторы симметрического оператора, соответствующие разным 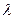, ортогональны.

Доказательство. Дано: 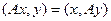, пусть первый вектор собственный и соответствует 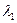, а второй 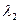. То есть верно: 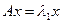и 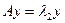. Тогда 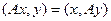можно записать в виде 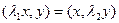, тогда 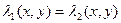, тогда 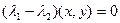. Собственные числа разные, поэтому первый множитель не равен 0, тогда 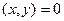. Скалярное произведение 0, векторы ортогональны.

Следствие. Для линейного оператора, матрица которого симметрична, существует ортогональный базис, состоящий из собственных векторов.

Квадратичные формы.

Билинейная форма, её задание с помощью матрицы.

Рассмотрим подробнее скалярное произведение типа 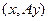, А - матрица некоторого линейного оператора. Произведение квадратной матрицы на столбец 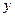это вектор-столбец, затем его скалярно умножаем на вектор 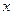, в итоге получится число. Таким образом, 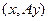это некоторая скалярная функция от 2 векторов. Она линейна по каждому аргументу: если на 1 или 2 месте сумма векторов, то результат тоже представляется в виде суммы. Обозначим 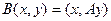и назовём эту функцию билинейной формой.

Подробнее при n=2 :

= = .

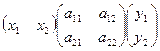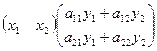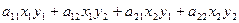При произвольном n: 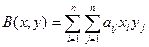здесь n² слагаемых.

Фактически, это обобщённое скалярное произведение. Обычное скалярное произведение можно задать таким же способом, но с единичной матрицей Е: 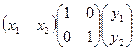= 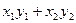. Это частный случай билинейной формы.

Теперь рассмотрим такой случай. Пусть билинейная форма вычисляется от 2 одинаковых векторов, 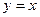. Обозначим 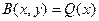и назовём эту функцию, отобрающую один вектор в число, квадратичной формой.

Квадратичная форма задаётся через скалярное произведение так: .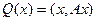

= .

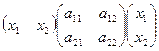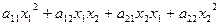Например, матрица 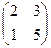задаёт такую квадратичную форму:

= = .

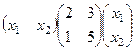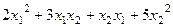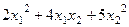Очевидно, 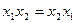, то есть эта группа из двух слагаемых 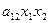и 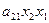может быть объединена. Коэффициенты 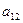и 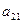распределить поровну. Так, 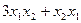это то же самое, что 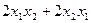. Но ведь тогда матрицу квадратичной формы можно сделать симметричной, перераспределить эквивалентные элементы с сохранением их суммы. Таким образом, квадратичную форму всегда можно задать симметричной матрицей. Эта же самая квадратичная форма может быть задана и такой матрицей: .

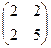Пример.Построить матрицу квадратичной формы

.

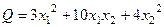Решение.Распределим поровну коэффициенты:

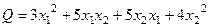. Каждый коэффициент, стоящий при 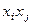, запишем на место .

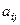Ответ: матрица: .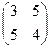

* Очевидно, если матрица диагональна, то 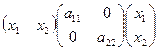= 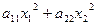квадратичная форма не содержит попарных произведений, а содержит только квадраты координат.

* Вспомним теорему 7 из прошлого §. Если матрица симметрична, то собственные векторы ортогональны.

* Вспомним также теорему 5 из прошлого §. Если в качестве нового базиса взять n собственных векторов, то матрица оператора в новом базисе будет диагональной.

Из всего сказанного следует, что квадратичную форму всегда можно привести к виду, не содержащему попарные произведения, а содержащему лишь квадраты, называется к «главным осям» (главные оси это направления, соответствующие собственным векторам).

Приведение к главным осям основано на поиске собственных чисел и векторов, примеры на эту тему решим подробно на практике.