Способы нахождения обратной матрицы
Матрицы
Определение 1. Прямоугольная таблица чисел вида
называется прямоугольной матрицей размера ,
где m - количество строк, а n - количество столбцов.
Определение 2. Числа, которые образуют матрицу, - aij
, где , , называются элементами матрицы.
Определение 3. Числа i и j называются индексами элемента aij,
i показывает, в какой строке расположен данный элемент
, а j - в каком столбце находится этот элемент.
Две матрицы считаются равными, если равны их
соответствующие элементы.
Виды матриц.
Если m=n, то матрица называется квадратной матрицей
порядка n.
Матрица размера Mx1 называется матрицей-столбцом.
Матрица размера 1xM называется матрицей-строкой.
Определение 1. Элементы матрицы, имеющие равные
индексы, образуют главную диагональ матрицы.
Определение 2. Квадратная матрица называется
диагональной, если все элементы вне ее главной
диагонали равны нулю.
Определение 3. Диагональная матрица n-го порядка,
у которой диагональные элементы равны единице,
называется единичной матрицей n-го порядк
а и обозначается Е.
Определение 4. Матрица называется матрицей
треугольного вида, если все элементы над (под) главной
диагональю равны нулю.
Операции над матрицами
Определение 1. Транспонированием матрицы называется
такое преобразование матрицы, при котором строки и
столбцы меняются ролями при сохранении номеров.
Транспонированная матрица обозначается АТ.
Для квадратной матрицы это преобразование эквивалентно
симметричному отображению относительно главной диагонали.
Определение 2. Суммой (разностью) двух матриц одинакового
порядка называется матрица того же порядка, каждый элемент
которой равен сумме (разности) соответствующих элементов
исходных матриц.
Определение 3. Произведением матрицы на число называется
матрица того же размера, каждый элемент которой равен
произведению соответствующего элемента исходной матрицы
на это число..
Определение 4. Произведением двух матриц А и В, размеры
которых заданы соотношением: количество столбцов первой
матрицы равно количеству строк второй, называется матрица С
, у которой количество строк равно количеству строк первой
матрицы, а количество столбцов равно количеству столбцов
второй. Каждый элемент данной матрицы равен сумме попарных
произведений элементов соответствующей строки первой
матрицы и элементов соответствующего столбца второй.
Приведем свойства операций над матрицами.
1)А · В не равно В · А
2)А+В = В+А
3) (А + В) +С = А + (В + С)
4) А · Е=Е · А=А.
Определители
Определение 1. Определителем n-го порядка матрицы А
называется число, равное алгебраической сумме n! Слагаемых
, каждое из которых равно произведению n элементов матрицы
А a1a1xa2a2x…anan, взятых по одному из каждой строки и
каждого столбца, причем каждое слагаемое берется со
знаком "+" или "-".
. Определитель второго порядка. n=2, 2!=1 · 2=2 слагаемых.
Определитель третьего порядка. n=3, 3!=1 · 2 · 3=6 слагаемых,
Обратная матрица
Обра́тная ма́трица — такая матрица A−1, при умножении
на которую, исходная матрица A даёт в результате
единичную матрицу E:
Квадратная матрица обратима тогда и только тогда
, когда она невырожденная, то есть её определитель
не равен нулю. Для неквадратных матриц и
вырожденных матриц обратных матриц не существует
. Однако возможно обобщить это понятие и ввести
псевдообратные матрицы, похожие на обратные по
многим свойствам.
Способы нахождения обратной матрицы
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём
матрицу A к единичной матрице методом Гаусса—Жордана.
После применения каждой операции к первой матрице
применим ту же операцию ко второй. Когда приведение
первой матрицы к единичному виду будет завершено,
вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет
умножаться слева на одну из элементарных матриц
(трансвекцию или диагональную матрицу с единицами на
главной диагонали, кроме одной позиции):
.
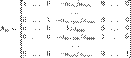 .
.
Вторая матрица после применения всех операций
станет равна /\ , то есть будет искомой.
Определение векторов
Вектор - это направленный прямолинейный отрезок,
т.е. отрезок, имеющий длину и определенное направление.
Графически вектор обозначается отрезком прямой,
на котором ставится стрелка, указывающая направление
вектора, в частности могут указываться начало и конец
вектора, например А - начало вектора, в В - конец вектора.
Длина вектора
Длина вектора равна расстоянию между его конечно и
начальной точками.
Векторы расположенные либо на одной прямой, либо на параллельных
прямых называются коллинеарными. Нулевой вектор считается
коллинеарным любому вектору. Среди коллениарных векторов
различают одинаково направленные (сонаправленные) и
противоположно направленные векторы.
Векторы называются компланарными, если они лежат либо на одной
плоскости, либо на прямых, параллельных одной и той же плоскости.
