Дифференциальные уравнения. 1. Равенство вида , содержащее независимую переменную x, искомую функцию y = y(x) и ее производные какого-либо порядка
1. Равенство вида 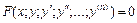 , содержащее независимую переменную x, искомую функцию y = y(x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
, содержащее независимую переменную x, искомую функцию y = y(x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
2. Натуральное число n, являющееся порядком старшей производной, называется порядком дифференциального уравнения.
3. Дифференциальным уравнением 1-го порядка называется уравнение вида 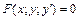 или в дифференциалах
или в дифференциалах 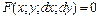 . Если эти равенства можно разрешить относительно производной, то их записывают в виде
. Если эти равенства можно разрешить относительно производной, то их записывают в виде 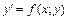 или
или 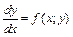 .
.
4. Решением дифференциального уравнения 1-го порядка называется функция y = j(x), имеющая непрерывную производную 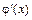 на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
5. Задача Коши для дифференциального уравнения 1-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальному условию y = y0 при x = x0.
6. Общим решением дифференциального уравнения 1-го порядка называется функция y = j(x; С), содержащая произвольную постоянную С и удовлетворяющая условиям: 1) при любых начальных условиях (x0; y0) уравнение y0 = j(x0; С) должно быть разрешимо относительно С так, что С = y(x0; y0); 2) при всех значениях постоянной С = y(x0; y0) функция y = j(x; y(x0; y0)) должна удовлетворять дифференциальному уравнению.
7. Всякое решение, получаемое из общего при фиксированном значении постоянной С называется частным решением дифференциального уравнения.
8. Уравнение вида 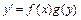 или
или 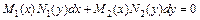 называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду
называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду 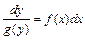 или
или 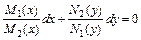 путем разделения переменных x и y и затем почленно интегрируются.
путем разделения переменных x и y и затем почленно интегрируются.
9. Уравнение вида 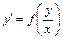 называется однородным дифференциальным уравнением. Используется замена:
называется однородным дифференциальным уравнением. Используется замена: 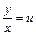 или
или 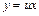 , где
, где 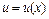 – новая неизвестная функция, тогда
– новая неизвестная функция, тогда 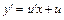 . Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле
. Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле 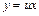 .
.
10. Уравнение вида 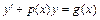 называется линейным дифференциальным уравнением. Используется метод Бернулли:
называется линейным дифференциальным уравнением. Используется метод Бернулли: 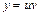 , где
, где 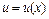 ,
, 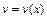 – новые неизвестные функции, тогда
– новые неизвестные функции, тогда 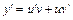 . Получаем:
. Получаем: 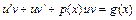 или
или 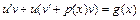 . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем 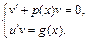 Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле
Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле 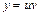 .
.
11. Уравнение вида 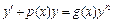 , где
, где 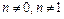 называется дифференциальным уравнением Бернулли. Используется метод Бернулли:
называется дифференциальным уравнением Бернулли. Используется метод Бернулли: 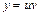 .
.
12. Дифференциальным уравнением 2-го порядка называется уравнение вида 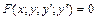 . Если уравнение можно разрешить относительно
. Если уравнение можно разрешить относительно 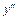 , то его записывают в виде
, то его записывают в виде 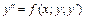 .
.
13. Решением дифференциального уравнения 2-го порядка называется функция y = j(x), имеющая непрерывные производные 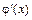 ,
, 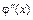 на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
14. Задача Коши для дифференциального уравнения 2-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальным условиям y = y0, 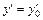 при x = x0.
при x = x0.
15. Общим решением дифференциального уравнения 2-го порядка называется функция y = j(x; С1; С2), содержащая две произвольные постоянные С1, С2 и удовлетворяющая условиям: 1) при любых начальных условиях 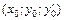 система уравнений
система уравнений 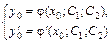 должна быть разрешима относительно постоянных С1, С2 так, что
должна быть разрешима относительно постоянных С1, С2 так, что 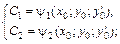 2) при всех значениях этих постоянных С1, С2 функция y = j(x; C1; C2) обращает дифференциальное уравнение в верное числовое равенство.
2) при всех значениях этих постоянных С1, С2 функция y = j(x; C1; C2) обращает дифференциальное уравнение в верное числовое равенство.
16. Всякое решение, получаемое из общего при фиксированных значениях постоянных С1, С2 называется частным решением дифференциального уравнения.
17. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка:
а) 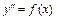 решается повторным интегрированием.
решается повторным интегрированием.
б) 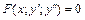 , явно не содержащее искомой функции
, явно не содержащее искомой функции 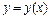 . Используется замена:
. Используется замена: 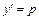 , где
, где 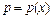 – новая неизвестная функция, тогда
– новая неизвестная функция, тогда 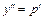 . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 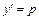 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
в) 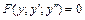 , явно не содержащее независимой переменной
, явно не содержащее независимой переменной 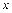 . Замена:
. Замена: 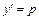 , где
, где 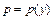 , тогда
, тогда 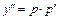 . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 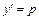 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
18. Линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида 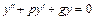 . Составляется характеристическое уравнение
. Составляется характеристическое уравнение 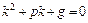 .
.
Если 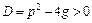 , то
, то 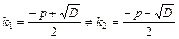 и общее решение исходного уравнения имеет вид:
и общее решение исходного уравнения имеет вид: 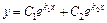 .
.
Если 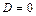 , то
, то 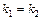 и
и 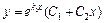 .
.
Если 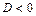 , то
, то 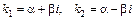 и
и 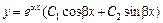 .
.
19. Линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами с правой частью специального вида называется уравнение вида 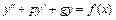 . Его общее решение ищется в виде
. Его общее решение ищется в виде 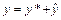 , где
, где 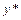 – общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:
– общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами: 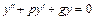 , а
, а 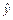 – какое-либо частное решение исходного уравнения.
– какое-либо частное решение исходного уравнения.
Если 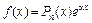 , где a – некоторое число, Pn(x) – многочлен степени n, то
, где a – некоторое число, Pn(x) – многочлен степени n, то 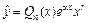 , где
, где 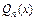 – многочлен степени
– многочлен степени 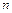 с неопределенными коэффициентами,
с неопределенными коэффициентами, 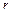 – число, равное кратности a как корня характеристического уравнения
– число, равное кратности a как корня характеристического уравнения 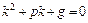 соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами 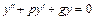 .
.
Если 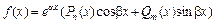 , где a, b – некоторые числа, Pn(x), Qm(x) – многочлены степени n и m соответственно, то
, где a, b – некоторые числа, Pn(x), Qm(x) – многочлены степени n и m соответственно, то 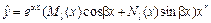 , где
, где 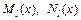 – многочлены степени
– многочлены степени 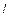 с неопределенными коэффициентами,
с неопределенными коэффициентами, 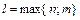 ,
, 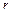 – число, равное кратности
– число, равное кратности 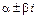 как корня характеристического уравнения
как корня характеристического уравнения 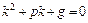 соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами 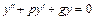 .
.
20. Система дифференциальных уравнений вида
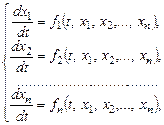
где 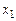 ,
, 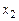 ,…,
,…, 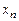 – неизвестные функции независимой переменной
– неизвестные функции независимой переменной 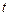 , называется нормальной системой.
, называется нормальной системой.
Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно 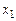 ,
, 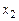 ,…,
,…, 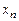 , то система дифференциальных уравнений называется линейной.
, то система дифференциальных уравнений называется линейной.
21. а) Если дана система 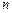 линейных дифференциальных уравнений с постоянными коэффициентами:
линейных дифференциальных уравнений с постоянными коэффициентами:
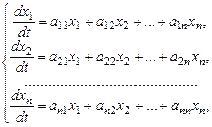
то эту систему можно записать в виде одного матричного дифференциального уравнения 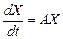 , где
, где
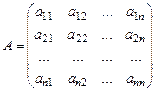 ;
; 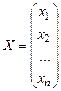 ;
; 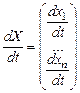 .
.
Решение системы ищем в виде 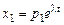 ,
, 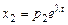 ,…,
,…, 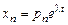 . Подставив значения
. Подставив значения 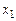 ,
, 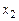 ,…,
,…, 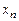 в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно
в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно 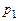 ,
, 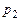 ,…,
,…, 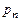 :
:
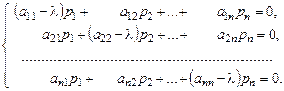
Система должна иметь ненулевое решение, поэтому для определения 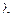 получаем уравнение
получаем уравнение 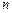 – й степени:
– й степени:
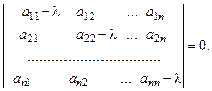
Пусть это характеристическое уравнение имеет 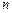 различных корней
различных корней 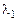 ,
, 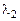 ,…,
,…, 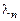 . Тогда система дифференциальных уравнений имеет
. Тогда система дифференциальных уравнений имеет 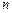 решений:
решений:
1-е решение, соответствующее корню 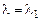 :
:
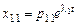 ;
; 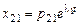 ;…;
;…; 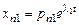
2-е решение, соответствующее корню 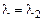 :
:
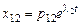 ;
; 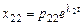 ;…;
;…; 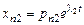 ;
;
…………………………………………………………………….
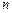 – е решение, соответствующее корню
– е решение, соответствующее корню 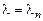 :
:
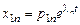 ;
; 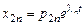 ;…;
;…; 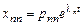 .
.
Получена фундаментальная система решений. Общее решение системы имеет вид
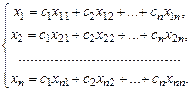
Такой способ решения называется решением линейных однородных систем дифференциальных уравнений с постоянными коэффициентами при помощи матриц (видоизмененный метод Эйлера).
б) Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению 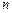 – го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
– го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
Ряды
1. Пусть дана бесконечная последовательность чисел а1, а2, …, аn. Числовым рядом называется сумма вида 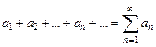 .
.
2. Если существует конечный предел 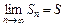 частичной суммы
частичной суммы 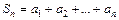 , то соответствующий числовой ряд
, то соответствующий числовой ряд 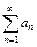 называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся.
называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся.
3. Основные свойства сходящихся числовых рядов:
а) Необходимый признак сходимости: если числовой ряд 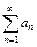 сходится, то
сходится, то 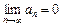 .
.
б) Достаточное условие расходимости: если 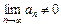 , то числовой ряд
, то числовой ряд 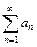 расходится.
расходится.
в) Если все члены сходящегося числового ряда 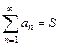 умножить или разделить на число
умножить или разделить на число 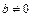 , то получится сходящийся ряд
, то получится сходящийся ряд 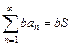 .
.
г) Если два сходящихся числовых ряда 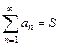 и
и 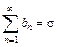 почленно сложить (или вычесть), то получатся сходящиеся ряды
почленно сложить (или вычесть), то получатся сходящиеся ряды 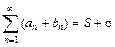 (или
(или 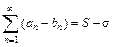 ).
).
