Пример 7. Гидролиз солей и буферные системы
1.Составьте ионно-молекулярные уравнения гидролиза солей NaNO2, K2CO3, FeSO4, ZnCl2 по всем возможным ступеням. Укажите реакцию среды полученных растворов. Напишите выражения и рассчитайте значения констант гидролиза этих соединений. Сделайте выводы по полученным величинам.
Решение. Все соли, независимо от их природы, при растворении в воде диссоциируют на ионы, а затем некоторые из них способны химически взаимодействовать с растворителем, отнимая у него ионы Н+ или ОН–. Из перечисленных в условии задачи солей две (натрия нитрит NaNO2 и калия карбонат K2CO3) образованы слабыми электролитами – кислотами, поэтому гидролизуются по анионному типу. В состав двух других (железа (2) сульфата FeSO4 и цинка хлорида ZnCl2) входят катионы слабых электролитов – оснований, следовательно, они гидролизуются по катионному типу. Составим соответствующие уравнения диссоциации и гидролиза солей.
1) NaNO2 = Na+ + NO2– - диссоциация полная и необратимая, а далее
NO2– + Н2О <=> НNO2 + ОН– - равновесное уравнение гидролиза.
Гидролиз обратим, т.к. образуется слабый электролит. Константа гидролиза характеризует состояние химического равновесия этого процесса и, согласно закону действующих масс, определяется следующим выражением:
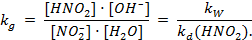
Значение ионного произведения воды при стандартных условиях равно, как мы знаем, 1,1·10-14, а значение kd азотистой кислоты найдем по таблице Приложения: kd(HNO2) = 6,9·10-4. Подставим эти значения в выражение для kg и рассчитаем константу:
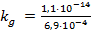 = 1,6·10-11.
= 1,6·10-11.
Расчеты показали, что для азотистой кислоты kd >> kg, поэтому равновесие в уравнении гидролиза будет смещено влево, т.е. гидролиз будет подавлен, рН = 7.
2) К2СО3 = 2К+ + СО32– - диссоциация необратимая, проходит в одну ступень,
а далее СО32– + Н2О <=> НСО3– + ОН– - 1-я ступень гидролиза.
Уравнение указывает на слабоосновный характер среды в результате связывания карбонат-ионов протонами воды, рН ≥ 7.
Для этой ступени kg1 = [HСO3–]·[OH–]/[СO32–]·[H2O] = kW/kd2(H2СO3).
Рассчитаем kg1, воспользовавшись справочными данными Приложения № 9:
kg1 = (1,1·10-14)/(4,7·10-11) = 2,34·10-4.
Как видно, kg1 >> kd2, равновесие смещено вправо в сторону гидролиза.
Возможен ли гидролиз карбонат-иона по второй ступени? Предположим, что
НСО3– + Н2О <=> Н2СО3 + ОН– - 2-я ступень гидролиза, среда основная, рН > 7.
Константа гидролиза по второй ступени будет определяться выражением:
kg2 = [H2СO3]·[OH–]/[НСO3–]·[H2O] = kW/kd1(H2СO3).
Рассчитаем вторую константу гидролиза, используя справочные данные:
kg2 = (1,1·10-14)/( 4,5·10-7) = 2,44·10-8.
Расчеты показали, что kg2 < kd1, а поэтому равновесие в уравнении гидролиза по второй ступени смещается влево. Процесс остановится на первой ступени и рН ≥ 7.
3) FeSO4 = Fe2+ + SO42– - диссоциация односторонняя необратимая.
Зная, что Fe(OH)2 - нерастворимое соединения, а серная кислота H2SO4 при диссоциации по 2-й ступени является слабым электролитом, предполагаем возможность протекания I-й ступени гидролиза по катионно-анионному типу:
Fe2+ + SO42– + Н2О <=> (FeOH)+ + (HSO4)–.
Выражение для константы гидролиза будет иметь вид:
kg1 = [(FeOH)+]·[ (HSO4)–]/[Fe2+]·[SO42–]·[H2O] = kW/kd2(Fe(OH)2)·kd2(H2SO4).
Рассчитаем значение первой константы гидролиза железа (2) сульфата, используя данные таблиц Приложения:
kg1 = (1,1·10-14)/(5,5·10-8)·(1,2·10-2) = 1,67·10-5.
Так как kg1 > kd2(Fe(OH)2), катион Fe2+ будет полностью связан в гидроксид-катион (FeOH)+, что же касается гидролиза аниона SO42–, то он невозможен, т.к. kd2(H2SO4) > kg1. Делаем вывод: гидролиз соли протекает только по катионному типу и тогда выражение его первой ступени станет иным:
Fe2+ + Н2О <=> (FeOH)+ + Н+ - I-я ступень гидролиза, среда слабокислотная, рН ≤ 7.
Уточним для неё и значение константы гидролиза:
kg1 = [(FeOH)+]·[H+]/[Fe2+]·[H2O] = kW/kd2(Fe(OH)2) = (1,1·10-14)/(5,5·10-8) = 0,2·10-6.
Проверим теперь, возможен ли более глубокий гидролиз катиона Fe2+.
(FeOH)+ + Н2О <=> Fe(OH)2 + H+ - II-я ступень гидролиза, среда кислотная, рН<7. Рассчитаем значение второй константы гидролиза:
kg2 = [Fe(OH)2]·[H+]/[(FeOH)+]·[H2O] = kW/kd1(Fe(OH)2),
kg2 = (1,1·10-14)/(1,2·10-2) = 9,17·10-13.
Сравнивая полученное значение константы гидролиза и константы диссоциации железа (2) гидроксида по первой ступени, легко сделать вывод о том, что kg2 << kd1(Fe(OH)2), следовательно, вторая ступень гидролиза проходить в этом растворе не будет, гидролиз остановится на первой ступени, среда останется слабокислотной, рН ≤ 7.
4) ZnCl2 = Zn2+ + 2Cl- - диссоциация полная и необратимая, затем
Zn2+ + H2O <=> (ZnOH)+ + H+ -1-я ступень гидролиза по катионному типу, рН ≤ 7;
kg1 = [(ZnOH)+]·[H+]/[Zn2+]·[H2O] = kW/kd2(Zn(OH)2).
Рассчитаем константу гидролиза, используя данные таблицы Приложения:
kg1 = (1,1·10-14)/(4,9·10-7) = 2,24·10-8.
Поскольку значения констант гидролиза и диссоциации не сильно отличаются, то гидролиз по первой ступени будет незначительным, избыток ионов Н+ почти не будет заметным, рН ≈ 7.
(ZnOH)+ + H2O <=> Zn(OH)2 + H+ - 2-я ступень гидролиза, для неё
kg2 = [Zn(OH)2]·[H+]/[(ZnOH)+]·[H2O] = kW/kd1(ZnOH)2).
Расчеты показывают, что kg2 = (1,1·10-14)/(1,3·10-5) = 8,46·10-10.
При этом kg2 << kd1(ZnOH)2), следовательно, равновесие в уравнении гидролиза полностью смещено влево, фактически гидролиза по второй ступени проходить не будет.
Ответ: а) NaNO2 диссоциирует необратимо, но гидролиз по аниону подавлен, среда нейтральная рН = 7, т.к. kd >> kg;
б) К2СО3 диссоциирует необратимо, гидролиз по аниону проходит только по первой ступени, среда слабоосновная рН ≥ 7;
в) FeSO4 диссоциирует необратимо, гидролиз идет только по катиону и останавливается на первой ступени, среда слабокислотная рН ≤ 7;
г) ZnCl2 диссоциирует необратимо, слабый гидролиз по катиону по первой ступени т.к. kg1 и kd2 отличаются незначительно, среда близкая к нейтральной, рН ≈ 7.
2.Определите возможные продукты при смешивании растворов Al(NO3)3 и Na2S. Составьте ионно-молекулярное и молекулярное уравнения гидролиза. Определите константы гидролиза солей при их совместном присутствии в растворе.
Решение. Как мы уже запомнили, процессу гидролиза предшествует диссоциация сильных электролитов, протекающая необратимо и в одну ступень. В нашем случае:
Al(NO3)3 = Al3+ + 3NO3–; Na2S = 2Na+ + S2–.
Гидролизу подвергается катион алюминия Al3+ и сульфид-анион S2–. Уравнения их гидролиза по первой ступени имеют вид:
Al3+ + H2O <=> (AlOH)2+ + H+; S2– + H2O <=> (HS)– + OH–.
В предыдущей задаче мы убедились в том, что если бы эти соли существовали в растворах раздельно, то гидролиз, по всей вероятности, остановился бы на первой ступени. Однако присутствие их в одном сосуде приводит к взаимному усилению гидролиза за счет связывания между собой высвобождающихся ионов Н+ и ОН– в слабый электролит Н2О. Оба гидролитических равновесия сдвигаются вправо, и гидролиз каждой из солей идет до конца:
(AlOH)2+ + H2O <=> (Al(OH)2)+ + H+,
и, наконец (Al(OH)2)+ + H2O <=> Al(OH)3↓ + H+;
то же и в случае аниона (HS)– + Н2О <=> H2S↑ + ОН–.
Образование нерастворимых и газообразных продуктов гидролиза делает его фактически необратимым, поэтому суммарное уравнение гидролиза можно записать в ионно-молекулярном и молекулярном виде и указать на необратимость этого процесса:
2Al3+ + 3S2- + 6H2O = 2Al(OH)3 ↓ + 3H2S↑;
2Al (NO3)3 + 3Na2S+ 6H2O = 2Al(OH)3 ↓ + 3H2S↑ + 6NaNO3.
Выражение для констант полного гидролиза солей имеет вид:
kg(Al3+) = kW/kd3·kd2·kd1(Al(OH)3); kg(S2-) = kW/kd2·kd1(H2S).
В таблицах Приложения находим соответствующие значения констант диссоциации по всем ступеням гидроксида алюминия и сероводорода, они равны:
kd1(Al(OH)3) = 8,3·10-9; kd2(Al(OH)3) = 2,1·10-9; kd3(Al(OH)3) = 1,0·10-9;
kd1(H2S) = 1,0·10-7; kd2(H2S) = 2,5·10-13.
Подставив найденные значения в уравнения для констант гидролиза, и помня, что kН2О = 1,1·10-14, рассчитаем величины констант гидролиза катиона Al3+ и аниона S2–:
kg(Al3+) = (1,1·10-14)/[(1,0·10-9)·(2,1·10-9)·(8,3·10-9)] = 6,31·1011;
kg(S2–) = (1,1·10-14)/[(2,5·10-13)·(1,0·10-7)] = 4,40·105.
Высокие значения констант гидролиза свидетельствуют о необратимости этих процессов.
Ответ: при смешивании растворов в результате необратимого и полного гидролиза по уравнению 2Al (NO3)3 + 3Na2S+ 6H2O = 2Al(OH)3 ↓ + 3H2S↑ + 6NaNO3.
образуется осадок алюминия гидроксида Al(OH)3 и выделяется газ сероводород H2S, значения констант гидролиза kg(Al3+) = 6,31·1011; kg(S2-) = 4,40·105.
3.Определите глубину гидролиза, рассчитайте степень гидролиза и рН 0,001 М раствора Fe2(SO4)3.
Решение. Вначале по уже разработанной нами схеме составим уравнение необратимой диссоциации и уравнения гидролиза железа (3) сульфата по возможным ступеням: Fe2(SO4)3 = 2Fe3+ + 3SO42–;
Fe3+ + SO42– + H2O <=> (FeOH)2+ + (HSO4)– - 1-я ступень, гидролиз по катионно-анионному типу;
(FeOH)2+ + H2O <=> (Fe(OH)2)+ + H+ - 2-я ступень по катионному типу;
(Fe(OH)2)+ + H2O <=> Fe(OH)3↓+ H+ - 3-я ступень с возможным выпадением осадка. Чтобы определить, на какой ступени гидролиз прекратится, нужно рассчитать константы гидролиза и сравнить их с константами диссоциации.
Выражение для константы гидролиза по 1-й ступени (катионно-анионный тип гидролиза) будет иметь вид:
kg1 = [(FeOH)2+]·[ (HSO4)-]/[Fe3+]·[SO42-]·[H2O] = kW/kd3(Fe(OH)3)·kd2(H2SO4).
Рассчитаем значение первой константы гидролиза железа (3) сульфата, используя данные таблиц Приложения: kd3(Fe(OH)3) = 1,5·10-12; kd2(H2SO4) = 1,2·10-2 и тогда kg1 = (1,1·10-14)/[(1,5·10-12)·(1,2·10-2)] = 0,61.
Учитывая то, что kg1 >> kd3(Fe(OH)3) и kg1 > kd2(H2SO4), катион Fe2+ и анион SO42–будут полностью связаны в гидроксид-катион (FeOH)2+ и гидро-анион (HSO4)–, т.е. гидролиз по первой ступени будет полным.
Гидролизу по второй ступени соответствует выражение для константы гидролиза:
kg2 = [Fe(OH)2+]·[H+]/[(FeOH)2+]·[H2O] = kW/kd2(Fe(OH)3).
Из таблицы Приложения находим kd2(Fe(OH)3) = 1,8·10-11, тогда
kg2 = (1,1·10-14)/(1,8·10-11) = 0,61·10-3.
И в данном случае kg2 >> kd2(Fe(OH)3), следовательно, и по второй ступени гидролиз будет полным.
Выражению для константы гидролиза по третьей ступени
kg3 = [Fe(OH)3]·[H+]/[Fe(OH)2+]·[H2O] = kW/kd1(Fe(OH)3)
при kd1(Fe(OH)3) = 4,8·10-11 соответствует значение kg3 = (1,1·10-14)/(4,8·10-11) = 0,23·10-3.
И в данном случае kg3 >> kd1(Fe(OH)3), следовательно, гидролиз Fe3+ будет полным и необратимым. Суммарное ионно-молекулярное уравнение гидролиза будет иметь вид:
Fe3+ + SO42– + H2O = Fe(OH)3↓+(HSO4)– + H+,
или в молекулярном виде
Fe2(SO4)3 + H2O = Fe(OH)3↓ + H2SO4.
Общая константа гидролиза определяется, как и в случае общей константы диссоциации (уравнение 26 теоретической части), по формуле:
kg = kg1·kg2·kg3 = (0,61)·(0,61·10-3)·(0,23·10-3) = 8,56·10-4.
Связь между константой гидролиза kg и степенью гидролиза β установлена законом Оставальда: kg = β2Сμ/(1 - β).
Решим его относительно степени гидролиза:
β2·10-3 = (8,56·10-4)(1-β) или β2 + 8,56β – 0,856 = 0, тогда β = 0,1 или β = 10%.
Для расчета рН такого раствора используем уравнение:
рН = 7 + ½рkd2(H2SO4) - ½pkd1(Fe(OH)3).
Подставим соответствующие значения и произведем расчеты:
рН = 7 - ½ℓg(1,2·10-2) + ½ℓg(4,8·10-11) = 7 - ½(-2 + 0,08) + ½(-11 + 0,68) = 7 + 0,96 - 5,12 = 2,84.
Ответ: гидролиз полный с образованием осадка Fe(OH)3, β = 10%; рН = 2,84.
4. При нагревании раствора гидролизующейся соли его рН увеличился с 10,5 до 11. Рассчитайте, во сколько раз изменилась степень гидролиза и константа гидролиза соли.
Решение. Если среда основная, значит, гидролиз протекает по анионному типу. Составим возможные уравнения диссоциации и гидролиза, упрощая выражения:
МеАn =Ме+ + An– и An– + Н2О <=> НАn + ОН–.
Из уравнения гидролиза следует, что Сμ(ОН–) = Сμ(НАn) и тогда по закону действующих масс для состояния равновесия
kg = Сμ2(ОН–)/Сμ(An–).
С другой стороны, используя физический смысл понятия степени гидролиза, можно записать Сμ(ОН–) = β·Сμ(An–), а из ионного произведения воды следует, что
Сμ(Н+) = kН2О/Сμ(ОН–) и тогда Сμ(Н+) = kН2О/β·Cμ(An–).
Поскольку kН2О и молярная концентрация растворенной соли Сμ(An–) остаются практически неизменными, то справедливо следующее равенство:
Сμ(Н+)1/Сμ(Н+)2 = β2/β1.
По условию задачи Сμ(Н+)1= 10-10,5 и Сμ(Н+)2 = 10-11, тогда β2/β1= 10-10,5/10-11 = 3,16. Следовательно, при нагревании степень гидролиза возросла в 3,16 раза.
Согласно закону Оствальда, константа гидролиза прямо пропорциональна квадрату степени гидролиза, т.е. kg = β2Cμ, откуда следует
(β2/β1)2 = kg2/kg1.
Решим это равенство относительно kg2/kg1 и получим:
kg2/kg1 = (3,16)2 = 9,99 ≈ 10.
Таким образом, при нагревании раствора константа гидролиза возросла в 10 раз.
Ответ: при нагревании раствора соли степень её гидролиза увеличилась в 3,16 раза, а константа гидролиза – в 10 раз.
5.Вычислите рН 0,2 М раствора муравьиной кислоты, к 1 л которого добавлено 3,4 г натрия формиата, если степень диссоциации соли равна 93%, а константа диссоциации кислоты kd(HCOOH) = 1,8·10-4. Объясните механизм буферного действия такой системы.
Решение. Система, состоящая из раствора слабого электролита и его соли с сильным электролитом называется буферной, она способна сохранять практически неизменной концентрацию ионов водорода при разбавлении водой или добавлении небольших количеств сильных кислот или щелочей.
В нашем случае к раствору слабого электролита – муравьиной кислоты НСООН добавлен сильный электролит – натрия формиат HCOONa. Образующиеся при его диссоциации формиат-ионы способны гидролизоваться, изменяя рН всей системы. В общей сложности в данной системе одновременно происходят три взаимосвязанных процесса:
1) НСООН <=> НСОО– + Н+,
2) HCOONa = HCOO– + Na+,
3) HCOO– + H2O <=> HCOOH + OH–.
Полная диссоциация соли по уравнению (2) подавляет диссоциацию кислоты по уравнению (1) и гидролиз НСОО– по уравнению (3).
PН буферной системы в случае кислотного буфера определяется по уравнению:
рН = pkd(НСООН) - ℓg [Cμ(НСООН)/Cμ(HCOO–)].
Для расчета рН по этому уравнению следует предварительно рассчитать молярную концентрацию раствора соли и анионов НСОО–:
Cμ(HCOONa) = m(HCOONa)/[M(HCOONa)·V(р-ра)]; Cμ(HCOONa) =3,4/(67·1)=0,05 моль/л. И тогда Cμ(HCOO–) = α· Cμ(HCOONa) = (0,93)·(0,05) = 0,046 моль/л.
Теперь рассчитаем рН раствора буферной системы:
рН = -ℓg(1,8·10-4) - ℓg(0,2/0,046) = (4 - 0,25) – 0,64 = 3,11.
Механизм буферного действия заключается в том, что при добавлении небольших количеств сильного электролита (кислоты или щелочи) и значительным увеличением концентрации Н+ или ОН– соответственно смещаются равновесия (3) или (1) вправо в связи с образованием более слабого электролита – воды. При этом образуется некоторое избыточное количество муравьиной кислоты (по уравнению 3), либо анионов соли (по уравнению 1), но рН раствора останется на прежнем уровне.
Ответ: рН = 3,11.
6. Рассчитайте буферную ёмкость по отношению к HCl и к NaOH раствора, содержащего в 1 л 1 моль хлорида аммония и 2 моль гидроксида аммония.
Решение.Буферная ёмкость системы характеризует способность буфера поддерживать постоянное значение рН при добавлении кислоты или щелочи. Эта способность выражается количеством вещества n кислоты или щелочи, которое необходимо добавить к 1 л буферного раствора, чтобы понизить (при добавлении кислоты) или повысить (при добавлении щелочи) рН раствора на единицу.
Для основного буфера рН вычисляется по уравнению
рН = 14 – рkd(осн) + ℓg [Cμ(осн)/Сμ(соли)].
Воспользуемся справочными данными Приложения для определения константы диссоциации гидроксида аммония kd(NH4OH) = 1,8·10-5, и данными условия задачи Сμ(NH4OH) = 2 моль/л, Сμ(NH4Cl) = 1 моль/л, подставим их в выражение для рН и произведем расчеты:
рН = 14 + ℓg(1,8·10-5) + ℓg(2/1) = 14 – 5 + 0,25 + 0,30 = 9,55.
Обозначим буферную ёмкость раствора по отношению к HCl через х моль. Тогда при добавлении х моль HCl к 1 л буферного раствора произойдет реакция
NH4OH + HCl <=> NH4Cl + H2O.
При этом концентрация соли увеличится до Сμ(NH4Cl) = (1 + х) моль/л, а концентрация основания уменьшится до Сμ(NH4OH) = (2 – х) моль/л. И тогда рН раствора должен понизиться на единицу, т.е. рН = 8,55. Подставим найденные значения в уравнение для рН и решим его относительно х:
8,55 = 14 + ℓg(1,8·10-5) + ℓg[(2-x)/(1+x)];
ℓg[(2 - x)/(1 + x)] = -0,7; (2 - x)/(1 + x) = 10-0,7 = 0,2; 2 – x = 0,2(1 + x); x = 1,50.
Таким образом, буферная ёмкость аммиачного буфера по отношению к HCl равна 1,50 моль/л.
Обозначим буферную ёмкость раствора по отношению к NaOH через у моль. Тогда при добавлении у моль NaOH к 1 л буферного раствора произойдет реакция
NH4Cl + NaOH <=> NH4OH + NaCl.
При этом концентрация соли уменьшится до Сμ(NH4Cl) = (1 – у) моль/л, а концентрация основания увеличится до Сμ(NH4OH) = (2 + у) моль/л, и рН раствора увеличится на единицу, т.е. рН = 10,55. Подставим найденные значения в уравнение для рН и решим его относительно у:
10,55 = 14 + ℓg(1,8·10-5) + ℓg[(2 + у)/(1 – у)]; ℓg[(2 + у)/(1 – у)] = 1,3;
(2 + у)/(1 – у) = 101,3 = 19,95; 2 + у = 19,95(1 – y); y = 0,86.
Следовательно, буферная ёмкость по отношению к NaOH равна 0,86 моль/л.
Ответ: nHCl = 1,50 моль на 1 л буферной системы, nNaOH = 0,86 моль на 1 л буферной системы.
