Решение линейных систем с помощью обратной матрицы
Рассмотрим линейную систему (2.3): 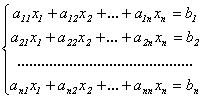 и введем следующие обозначения:
и введем следующие обозначения:
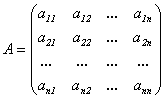 - матрица системы,
- матрица системы, 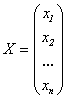 - столбец неизвестных,
- столбец неизвестных,
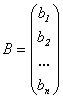 - столбец свободных членов. Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В. (3.1)
- столбец свободных членов. Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В. (3.1)
Пусть матрица А – невырожденная, тогда существует обратная к ней матрица 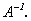
Умножим обе части равенства (3.1) слева на 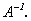 Получим
Получим
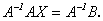
Но 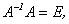 тогда
тогда 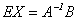 , а поскольку
, а поскольку 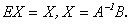 (3.2)
(3.2)
Итак, решением матричного уравнения (3.1) является произведение матрицы, обратной к А, на столбец свободных членов системы (2.3).
Пример. Вернемся к системе 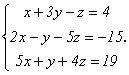
Для нее 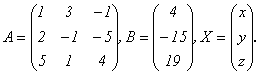
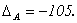 Найдем
Найдем 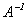 :
:
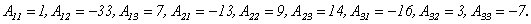
Следовательно, 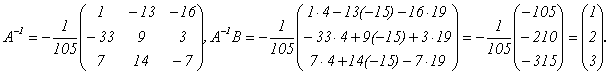
Таким образом, х = 1, у = 2, z = 3.
Лекция 4.
Ранг матрицы. Теорема о ранге. Вычисление ранга матрицы. Совместность систем линейных уравнений. Теорема Кронекера-Капелли. Структура общего решения однородной системы линейных уравнений. Общее решение неоднородной системы линейных уравнений.
Определение 4.1. Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и kстолбцов данной матрицы.
Замечание. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.
Определение 4.2. Ранг матрицы – это порядок ее наибольшего ненулевого минора.
Обозначения: r(A), R(A), Rang A.
Замечание. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей.
Примеры:
1. 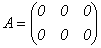 , r(A)=0.
, r(A)=0.
2. 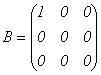 . Матрица В содержит единственный ненулевой элемент -
. Матрица В содержит единственный ненулевой элемент - 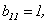 являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
3. 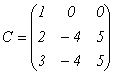 . Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.
. Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.
Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, 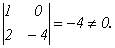 Значит,r(C)=2.
Значит,r(C)=2.
4. 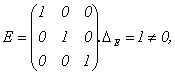 следовательно, r(E)=3.
следовательно, r(E)=3.
Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже 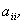 равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
1) транспонирование
2) умножение строки на ненулевое число
3) перестановка строк
4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число
5) вычеркивание нулевой строки.
Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.
Пример. Найдем ранг матрицы 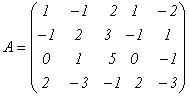 . Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:
. Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:
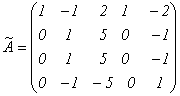
 .
.
Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:
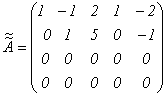 .
.
После вычеркивания нулевых строк получим матрицу размерности 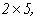 для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
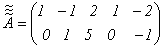 .
.
Ее минор 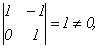 следовательно,
следовательно, 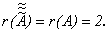
Теорема о ранге.
Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.
Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).
В противном случае строки (столбцы) называются линейно независимыми.
Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных.
Теорема 4.1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).
Доказательство (для строк).
1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.
2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.
Докажем это свойство для строки, не входящей в базисный минор.
Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:
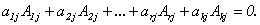 Поскольку
Поскольку 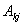 является базисным минором,
является базисным минором, 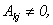 поэтому, разделив полученное равенство на
поэтому, разделив полученное равенство на 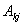 , найдем, что
, найдем, что
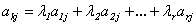 для всех j=1,2,…,n, где
для всех j=1,2,…,n, где 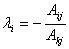 . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.
. Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.
