Элементы линейной алгебры и аналитической геометрии

Системы координат на прямой, плоскости и в пространстве. Пространства 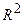и 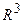. Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора. Понятие о векторных диаграммах в науке и технике (диаграммы сил, моментов сил, электрических токов, напряжений и др.). Координаты центра масс.

Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Условие ортогональности двух векторов. Механический смысл скалярного произведения.

Определители второго и третьего порядков, их свойства. Алгебраические дополнения и миноры. Определители n-го порядка. Вычисление определителя разложением по строке (столбцу).

Векторное произведение двух векторов, его свойства. Условие коллинеарности двух векторов. Геометрический смысл определителя второго порядка. Простейшие приложения векторного произведения в науке и технике: моменты сил, сила, действующая на проводник с током в магнитном поле, скорость точки вращающегося тела, направление распространения электромагнитных волн, понятие о явлении гироскопии.

Смешанное произведение векторов. Геометрический смысл определителя третьего порядка.

Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.

Кривые второго порядка: окружность, эллипс, гипербола, парабола, их геометрические свойства и уравнения. Технические приложения геометрических свойств кривых (использование фокальных свойств, математические модели формообразования биологических, технических и других объектов).

Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью.

Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Эллипсоид. Гиперболоиды. Параболоиды. Геометрические свойства этих поверхностей, исследование их формы методом сечений. Технические приложения геометрических свойств поверхностей (использование фокальных свойств, модели строительных конструкций, физические модели элементов и т.п.).

Полярные координаты на плоскости. Спираль Архимеда.

Цилиндрические и сферические координаты в пространстве. Различные способы задания линий и поверхностей в пространстве.

Матрицы, действия с ними. Понятие обратной матрицы.

Системы двух и трех линейных уравнений. Матричная запись системы линейных уравнений. Правило Крамера. Система m линейных уравнений с n неизвестными. Метод Гаусса. Нахождение обратной матрицы методом Гаусса.

Пространство 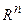. Линейные операции над векторами. Различные нормы в 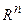. Скалярное произведение в .

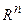Линейные и квадратичные формы в 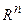. Условие знакоопределенности квадратичной формы.

Понятие линейного (векторного) пространства. Вектор как элемент линейного пространства. Примеры. Линейные операторы. Примеры линейных операторов. Применение линейных операторов для моделирования различных процессов.

Введение в математический анализ

Элементы математической логики: необходимое и достаточное условия. Прямая и обратная теоремы. Символы математической логики, их использование. Бином Ньютона. Формулы сокращенного умножения.

Множество действительных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики.

Числовые последовательности, их роль в вычислительных процессах. Предел числовой последовательности. Стабилизация десятичных знаков у членов последовательности, имеющей предел. Существование предела монотонной ограниченной последовательности.

Сложные и обратные функции, их графики. Класс элементарных функций.

Предел функции в точке. Предел функции в бесконечности. Пределы монотонных функций.

Непрерывность функций в точке. Непрерывность основных элементарных функций.

Бесконечно малые функции, их свойства. Сравнение бесконечно малых. Символы 0 и О.

Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.