Можно создавать различные виды графиков – поверхность, цилиндрическая, конусная и др

ОТЧЕТ

О выполнении лабораторной работы по информатике №8

Тема: Табличный процессор MS EXCEL.Математические расчеты. Создание макроса.

Выполнил: студент гр. 12Т1 О.Ю. Сидорова

Проверил: преподаватель О.А. Баранова

Пенза

Цель работы:

- ознакомиться с возможностями Excel для решения математических задач;

- освоить методы построения графиков математических функций;

- освоить встроенные функции для работы с матрицами;

- освоить приемы работы с командами Подбор параметра и Поиск решения.

Выполнение заданий.

1.

2.

3.

4.

Ответы на контрольные вопросы.

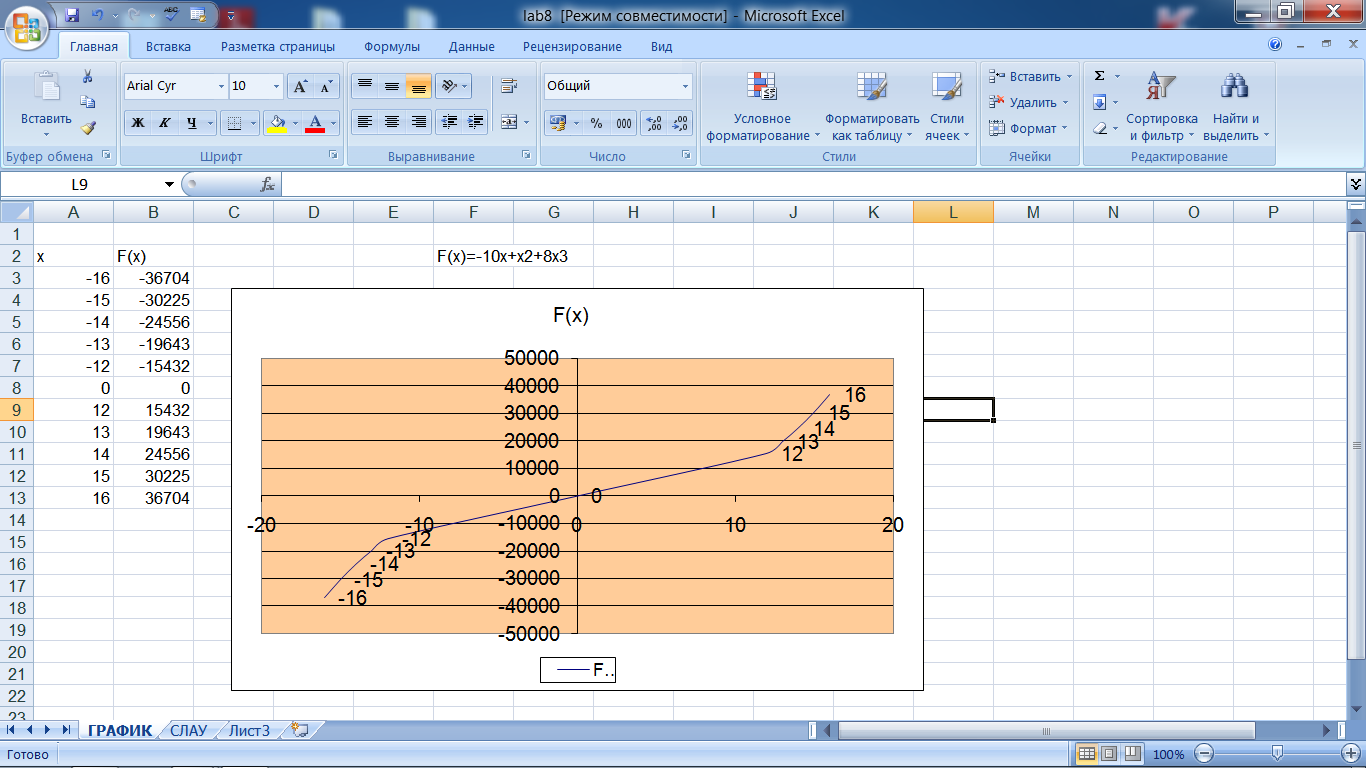
1.График функции строится по созданной таблице значений функции. Значения аргумента задаются методом Автозаполнения (в виде арифметической прогрессии). Шаг выбирают небольшим, чтобы таблица значений функции отражала её поведение на интервале табуляции. Затем вызывается Мастер диаграмм.

Для построения графиков функций используются два типа диаграмм: График и Точечная.

Можно создавать различные виды графиков – поверхность, цилиндрическая, конусная и др.

2.При выборе диаграммы типа График следует выделить только диапазон, содержащий значения функции. Подпись значений аргументов по оси x добавляется на вкладке Ряд в поле Подпись по оси X диалогового окна Исходные данные (Мастер диаграмм, шаг 2).

При выборе диаграммы типа Точечнаядостаточно выделить ячейку, содержащую первое значение аргумента, на графике отобразится весь диапазон таблицы значений функции; подписи по оси аргументов x будут соответствовать табличным значениям аргумента.

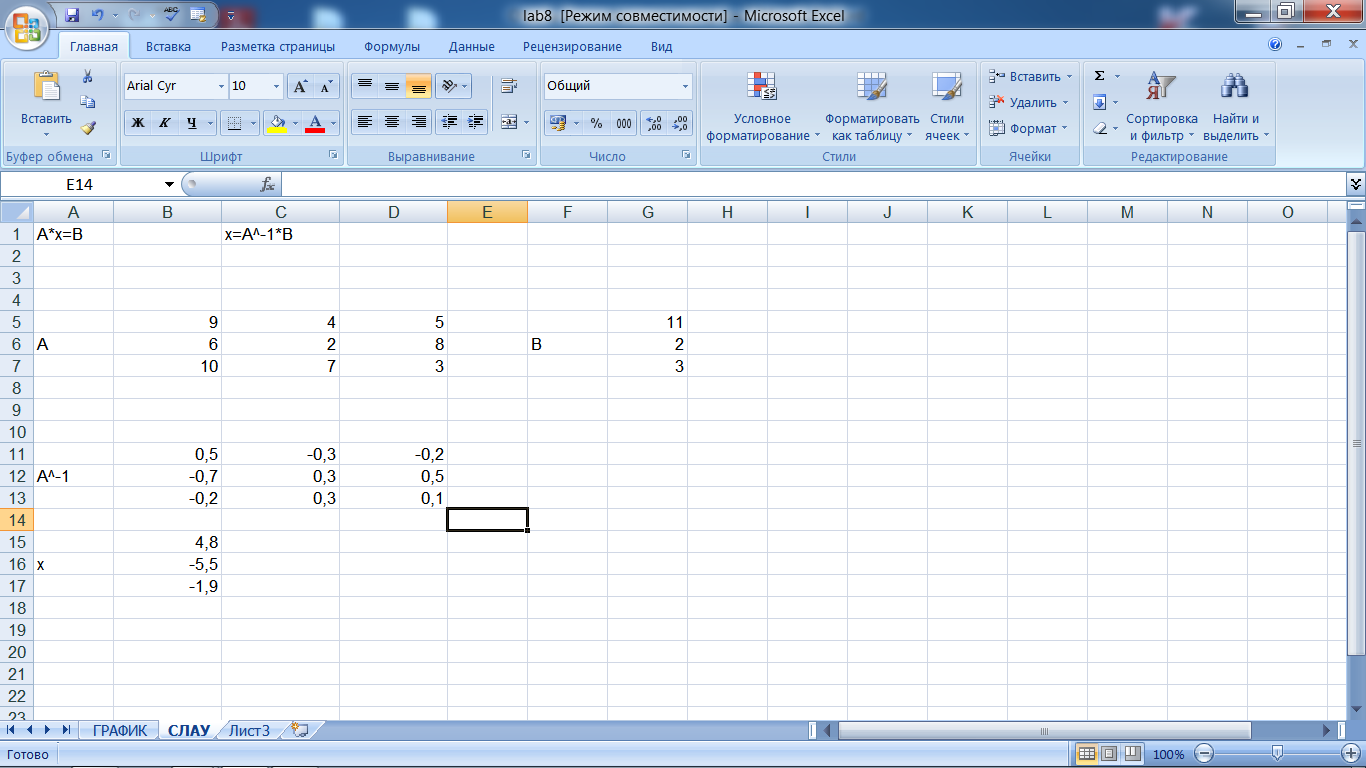
3. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Метод Гаусса - один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры (теория и вычисление определителей, решение систем линейных уравнений, вычисление ранга матрицы и обратной матрицы, теория базисов конечномерных векторных пространств и т.д.).
Задача поиска решений системы линейных уравнений имеет не только самостоятельное значение, но часто является составной частью алгоритма решения многих нелинейных задач. Основные методы решения СЛУ:
метод Гаусса;
метод обращения матрицы;
итерационные методы.
Матрица A с элементами a_ij называется ступенчатой, если она обладает следующими двумя свойствами:
1.если в матрице есть нулевая строка, то все строки ниже нее также нулевые;
2.пусть a_ij не равное 0 -- первый ненулевой элемент в строке с индексом i, т.е. элементы a_il = 0 при l < j. Тогда все элементы в j-м столбце ниже элемента a_ijравны нулю, и все элементы левее и ниже a_ij также равны нулю: a_kl = 0 при k > i и l =< j. Преобразование первого рода :две строки матрицы меняются местами, и при этом знаки всех элементов одной из строк изменяются на противоположные.
Преобразование второго рода:к одной строке матрицы прибавляется другая строка, умноженная на произвольное число.
Элементарные преобразования сохраняют определитель и ранг матрицы, а также множество решений линейной системы. Алгоритм Гаусса приводит произвольную матрицу элементарными преобразованиями к ступенчатому виду. Для ступенчатой квадратной матрицы определитель равен произведению диагональных элементов, а ранг - числу ненулевых строк (рангом по определению называется размерность линейной оболочки строк матрицы).

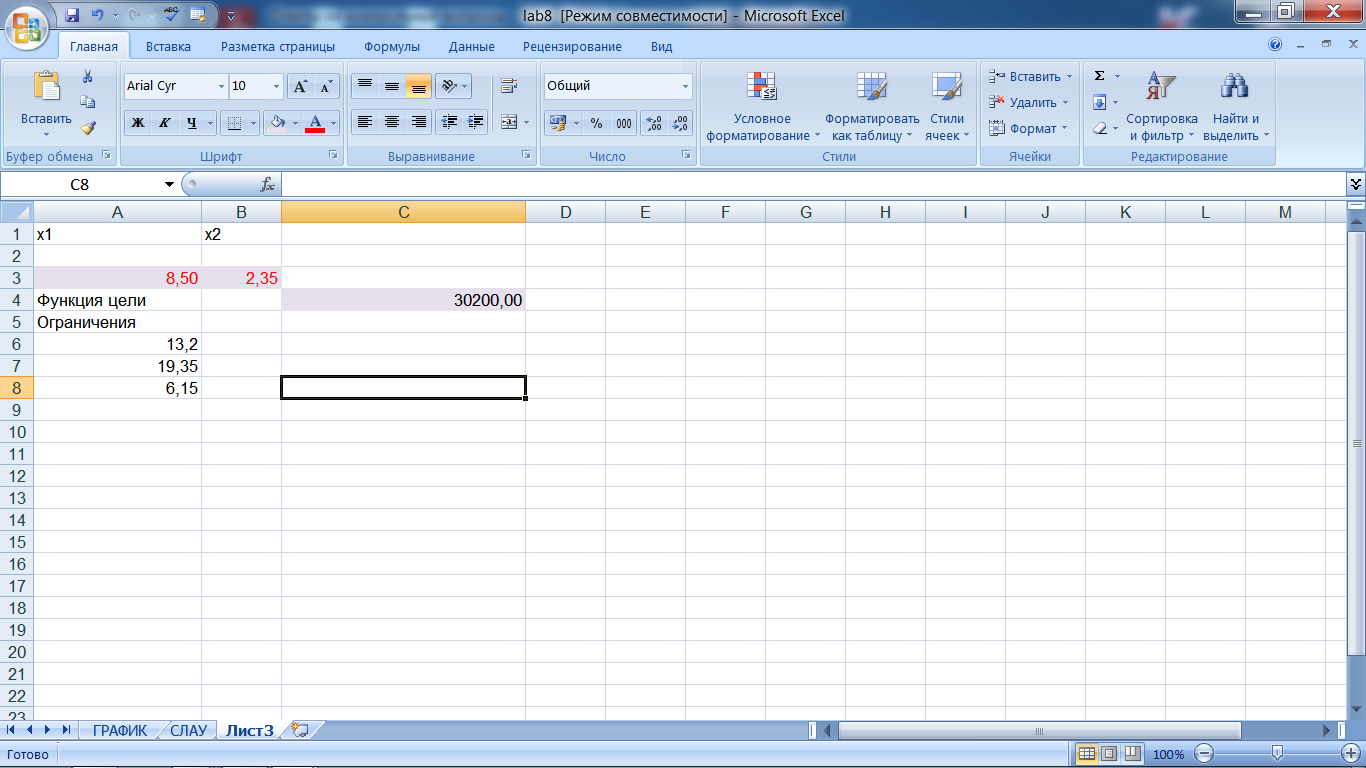
4. При проектировании и эксплуатации технических систем постоянно приходится решать задачи поиска наилучшего решения из некоторого множества допустимых решений. Такое решение называют оптимальным, процесс поиска такого решения - оптимизацией, а задачи, в которых ищется такое решение – оптимизационными задачами.

5. Основной командой для решения оптимизационных задач в Excel является команда Сервис/Подбор параметра. Эта команда определяет неизвестную величину, приводящую к требуемому результату.
Если команда Подбор параметра отсутствует в меню Сервис, выполните команду Сервис/Надстройка и установите флажок Пакет анализа в окне диалога Надстройка
Для работы с командой Подбор параметра необходимо подготовить лист, чтобы в листе находились:

- формула для расчета;

- пустая ячейка для искомого значения;

- другие величины, которые используются в формуле.

Ссылка на пустую ячейку должна обязательно присутствовать в формуле, так как именно она является переменной, значение которой ищет Excel. Во время подбора параметра в переменную ячейку непрерывно заносятся новые значения, пока не будет найдено решение поставленной задачи.

6.

· шаблоны Word (расширения DOT, DOTX, DOTM)

· книги Excel (расширения XLS, XLSX, XLSM, XLSB)

· шаблоны Excel (расширения XLT, XLTX, XLTM)

· текстовые документы (расширения TXT, DAT, XML и т.д.)

7.Форма – это защищенный документ особого рода, который содержит поля для ввода информации. Любой документ, который содержит поля формы, считается формой.

Поле формы – это особое поле в документе, которое позволяет выполнить одно из трех действий: ввести текст, сбросить/установить флажок, выбрать значение из раскрывающегося списка.

Структура многих форм задается с помощью таблиц, потому что ячейки таблицы отлично подходят для размещения, как меток полей, так и информационных полей. Кроме того, таблицы позволяют ввести в форму затенение и обрамление.

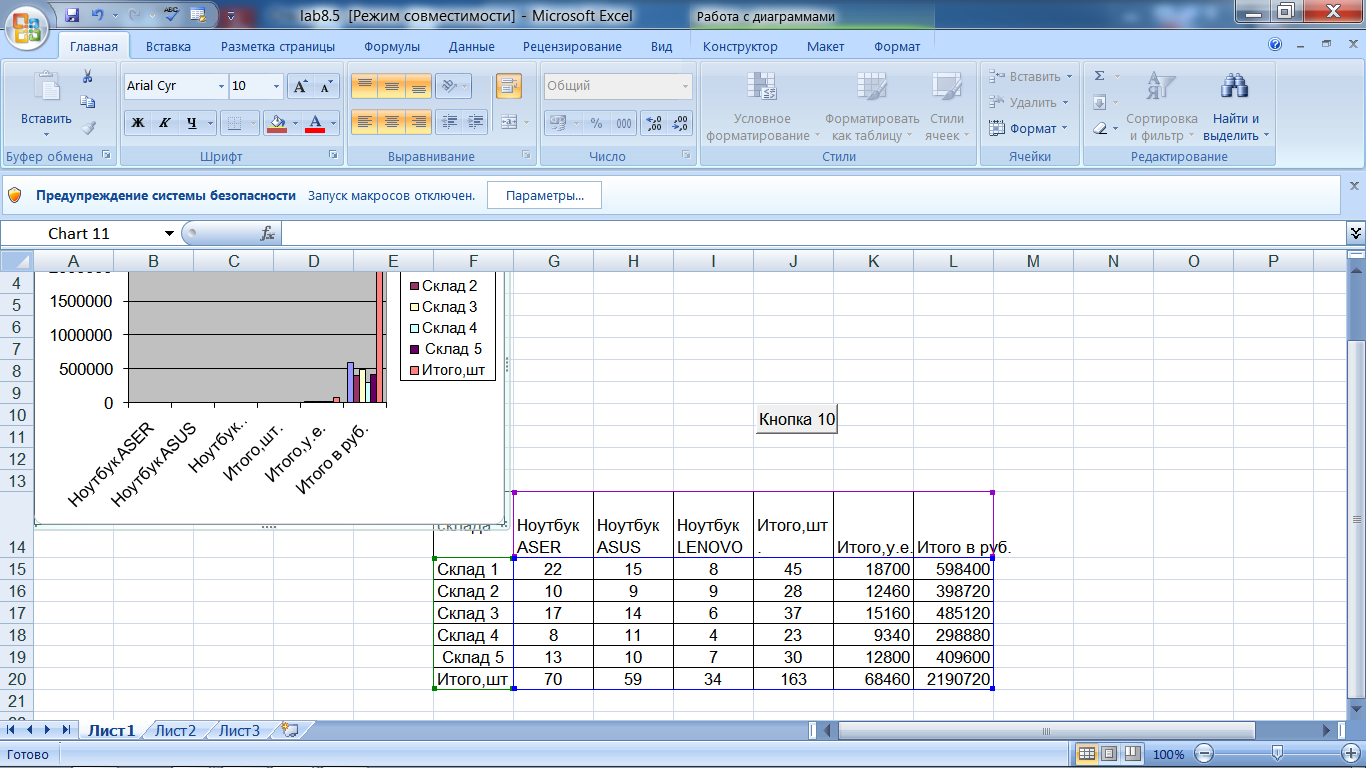
8.Когда следует использовать элементы управления панели инструментов «Формы». Элементы управления панели инструментов Формы следует использовать, если требуется записать все макросы для формы без написания или изменения кода макросов в VBA. Элементы управления панели инструментов Формы можно также использовать на листах диаграмм.

Элементы управления представляют собой графические объекты, помещаемые в форму для отображения или ввода данных, выполнения действий или облегчения чтения формы. Данные объекты включают надписи, поля со списками, переключатели и флажки, кнопки и многое другое. Элементы управления позволяют пользователю запускать макросы или веб-сценарии путем нажатия, установки или выбора соответствующих элементов управления.

9.

1. В главном меню выбираем вкладку "Рецензирование", затем на ленте в группе "Изменения" кликаем по пункту "Защитить лист".

2. В открывшемся окне "Защита листа" устанавливаем опцию "Защитить лист и содержимое защищаемых ячеек". При необходимости в поле "Пароль для отключения защиты листа" устанавливаем пароль. Не зная его, будет невозможно отключить защиту листа. По окончанию кликаем на кнопку "ОК" для защиты листа или "Отмена" для отказа от этого.

3. Если в поле "Пароль для отключения защиты листа" установлен пароль, то откроется окно "Подтверждение пароля". Повторяем введенный пароль в поле "Введите пароль еще раз" и кликаем на кнопку "ОК" для защиты листа или на кнопку "Отмена" для отказа от этого.

4. При попытке изменения содержимого ячеек на защищенном листе появляется окно, предупреждающее о необходимости предварительного снятия защиты листа.

5. Для снятия защиты листа в главном меню выбираем вкладку "Рецензирование", затем на ленте в группе "Изменения" кликаем по пункту "Снять защиту листа".

6. Если ранее был установлен пароль, в появившемся окне "Снять защиту листа" вводим установленный пароль и кликаем на кнопку "ОК" для снятия защиты листа или на кнопку "Отмена" для отказа от этого.

Вывод: В ходе лабораторной работы, я ознакомилась с возможностями Excel для решения математических задач; освоила методы построения графиков математических функций; освоила встроенные функции для работы с матрицами; освоила приемы работы с командами Подбор параметра и Поиск решения.