Связь случайных процессов и дифференциальных уравнений

История рождения метода Монте-Карло

Метод Монте-Карло (методы Монте-Карло) — общее название группы численных методов, основанных на получении большого числа реализаций случайного (стохастического) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в областях физики, математики, экономики, оптимизации, теории управления и др.

Алгоритм Буффона для определения числа Пи

Случайные величины использовались для решения различных прикладных задач достаточно давно. Примером может служить способ определения числа Пи, который был предложен Буффоном еще в 1777 году. Суть метода была в бросании иглы длиной N на плоскость, расчерченную параллельными прямыми, расположенными на расстоянии d друг от друга (см. Рис. 1).

рис.1. Метод Буффона

Вероятность того, что отрезок пересечет прямую связана с числом Пи:

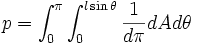, где

• A — расстояние от начала иглы до ближайшей к ней прямой;
• θ — угол иглы относительно прямых.

Этот интеграл просто взять: 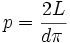(при условии, что d > L), поэтому подсчитав долю отрезков, пересекающих прямые, можно приближенно определить это число. При увеличении количества попыток точность получаемого результата будет увеличиваться.

В 1864 году капитан Фокс, выздоравливая после ранения, чтобы как-то занять себя, реализовал эксперимент по бросанию иглы. Результаты представлены в следующей таблице:

	Число бросаний	Число пересечений	Длина иглы	Расстояние между прямыми	Вращение плоскости	Значение Пи
Первая попытка					отсутствует	3.1780
Вторая попытка					присутствует	3.1423
Третья попытка					присутствует	3.1416

Комментарии:

• Вращение плоскости применялось (и как показывают результаты — успешно) для того, чтобы уменьшить систематическую ошибку.
• В третьей попытке длина иглы была больше расстояния между линиями, что позволило не увеличивая числа бросаний эффективно увеличить число событий и повысить точность.

Связь случайных процессов и дифференциальных уравнений

Создание математического аппарата случайных методов началось в конце 19го века. В 1899 году лорд Релей показал, что одномерное случайное блуждание на бесконечной решетке может давать приближенное решение параболического дифференциального уравнения. Колмогоров в 1931 году дал большой толчок развитию случайных подходов к решению различных математических задач, поскольку он сумел доказать, что цепи Маркова связаны с некоторыми интегро-дифференциальными уравнениями. В 1933 году Петровский показал, что случайное блуждание, образующее Марковскую цепь асимптотически связано с решением эллиптического дифференциального уравнения в частных производных. После этих открытий стало понятно, что, случайные процессы можно описывать дифференциальными уравнениями и, соответственно, исследовать при помощи хорошо на тот момент разработанных математических методов решения этих уравнений.