Все рисунки должны иметь заголовок, номер, оси. Рисунки, на которых приведены несколько функций, должны иметь легенду. Графики не должны быть угловатыми
Задания.
1. Вычислить точное и приближенное (c тоностью ε=0.0001) значения выражений
arccos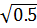 
-arcctg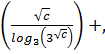 
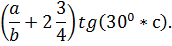
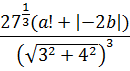
2. Пользуясь палитрой «Greek» записать формулы. Уметь давать названия буквам греческого алфавита
𝜲(t)=𝜆 sin(ξ 
), 𝜱(t)= 
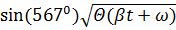
3. Упростить выражение
,
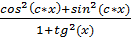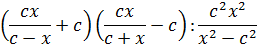
4. Задайте переменную x и присвойте ей значение b+0.5. Задайте переменную y и присвойте ей значение a. Задайте переменную z и присвойте ей значение c. Найдите точные значения выражений
24ctg(x)tg(x)+24y+6π-z,
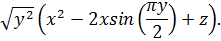
5. Найти все точки, в которых многочлен
.
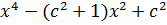обращается в ноль. Разложить многочлен на множители.
6. Сделайте указанную подстановку и упростите результат
, 
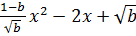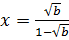
7. Упростите выражение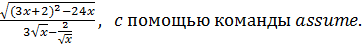 
8. Записать функцию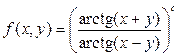 
в виде функционального оператора (воспользуйтесь панелью Expression «f:=(x,y)->z») и вычислите ее значения при x=1, y=0 и при 
, 
.
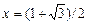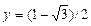9. Записать функцию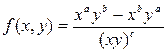 
с помощью оператора присваивания и вычислите ее значение при x=d, y=1/d.
10. Построить треугольник, стороны которого образуют прямые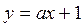 
, 
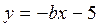и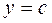 
.
11. Построить на одном рисунке графики функции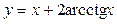 
и ее асимптот 
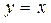и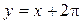 
. Установить следующие параметры: цвет основной линии – голубой, асимптот – красный; толщина основной линии – 3, асимптоты – обычной толщины, пунктирной линии; масштаб по координатным осям – одинаковый. Сделать легенду.
12. Построить двумерный график неявной функции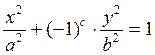 
. В заголовке указать название линии. Сделать координатную сетку.
13. Постройте на плоскости кривую, заданную в полярных координатах
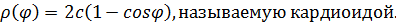
14. Постройте на плоскости кривую, заданную в параметрическом виде
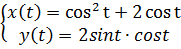
15. Построить график поверхности и определить ее вид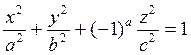 
. В заголовке указать ее вид.
16. Построить в одной системе координат графики поверхносте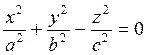й 
и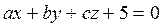 
и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение. Какая кривая получается при пересечении данных двух плоскостей.
17. Построить график функции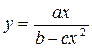 
со всеми своими асимптотами на оптимальном промежутке. Указать точки разрыва, определить их род.
18. Найти все точные решения системы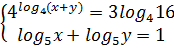 
.
19. Найти все решения тригонометрического уравнения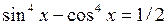 
.
20. Построить на одном графике две функции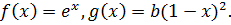 
Найти решение (c тоностью до ε=0.001) уравнения 
.
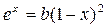21. Решить неравенство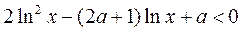 
.
22. Решить систему неравенств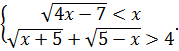 
ПРИЛОЖЕНИЕ 1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Национальный исследовательский университет «МЭИ»
в г. Смоленске
Кафедра
Высшей математики
Лабораторная работа №1
по дисциплине «Математика»
Вариант (указать номер по журналу)
Тема:
Студент группы ЭO-00 Иванов Александр
Преподаватель Винокурова А.С.
Смоленск 2011