Дискретное логистическое отображение

xn+1 = lxn(1– xn)

здесьl = 4r.

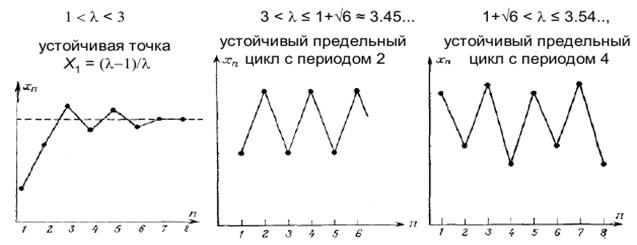
Зависимость динамики логистического отображения x_n от номера шага n.

а) устойчивая неподвижная точка (период 1);

(б) предельный цикл периода 2;

(в) предельный цикл периода 4.

%logistic_guld

clear all

r=[0.1 0.6 0.8 0.9];

for i=1:4

clear x

x(1)=0.75;

for n=2:25%150

l(i)=4*r(i);

x(n)=4*r(i)*x(n-1)*(1-x(n-1));

end

plot(x)

ss=num2str(r(i));

ssl=num2str(l(i));

title(['r = ' ss ' lambda = ',ssl])

xlabel('n');

ylabel('x');

grid on

figure

end

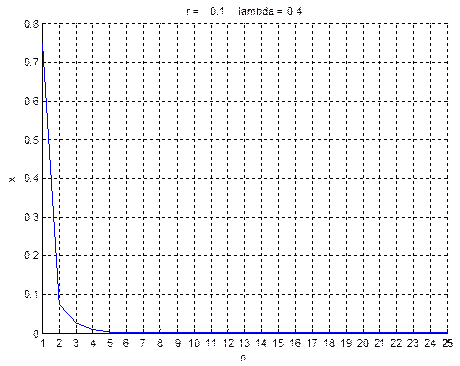
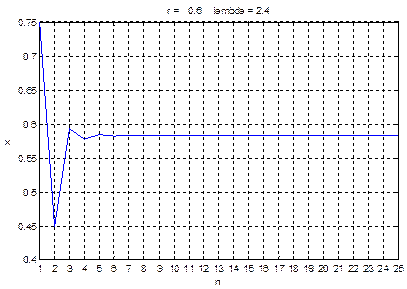
Рнс. 8.1,а. График итерированных значений х в зависимости от номера итерации для случаев r = 0.1 и r = 0.6.

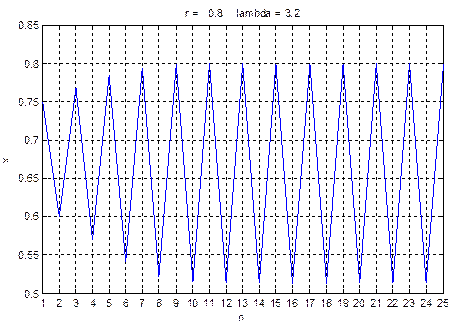
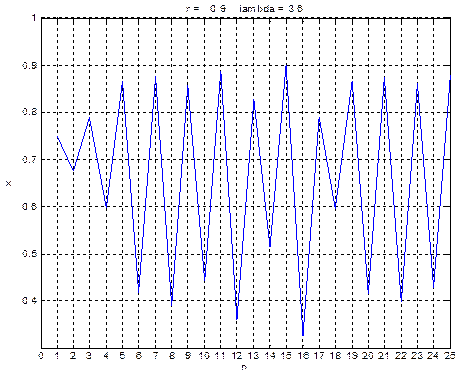
Рис. 8.1,6. График итерированных значений х в зависимости от номера итерации для случаев r = 0.8 и r = 0.9.

Много интересных свойств стандартного отображения были открыты Фейгенбаумом в 1978г. с помощью программируемого калькулятора.

Заметим, что несколько начальных итераций отображения f(х) ведут себя странным образом, но, тем не менее, за исключением случая r = 0.9, проявляется некая закономерность. Начальный отрезок последовательности называется переходным режимом, а остальная часть является установившимся режимом. Последовательность значений х_п называется орбитой отображения.

ЗАДАЧА 8.1. Исследование удвоения периода

а. Изучите динамическое поведение стандартного отображения (8.6) для значений параметра r = 0.2 и r = 0.24 и для различных значений источника x₀. Покажите, что х = 0 является устойчивой неподвижной точкой. Иначе говоря, для достаточно малого значения параметра r итерации х сходятся к х = 0 независимо от начального условия x₀. В том случае, когда переменная представляет собой численность популяции насекомых, качественно охарактеризуйте динамику этой популяции.

б. Исследуйте динамическое поведение стандартного отображения (8.6) для значений параметра r = 0.26, 0.5, 0.7, 0.72, 0.74 и 0.748. (В случае r = 0.748 для сходимости итерационного процесса необходимо приблизительно 1000 итераций.) Сходится ли процесс к значению х = 0? Неподвижная точка называется неустойчивой, если для почти всех значений х₀ итерационный процесс расходится.

Свидетельствуют ли ваши результаты о том, что х = 0 – неустойчивая неподвижная точка? Покажите, что через много поколений итерированные значения переменной х постоянны, т.е. динамический режим является стационарным или имеет период, равный 1. Каковы устойчивые неподвижные точки для различных значений параметра r?

Последовательность итераций x₀, х₁, …, x_n называется орбитой, или траекторией х. Покажите, что для любого из предложенных значений параметра r орбиты х по прошествии начального переходного периода не зависят от начального значения.

в. Исследуйте динамическое поведение стандартного отображения (8.6) для значений параметра r = 0.752, 0.76, 0.8 и 0.862. (В случае r = 0.752 для сходимости итерационного процесса необходимо приблизительно 1000 итераций.) Покажите, что если параметр становится чуть больше 0.75, то после переходного режима х осциллирует между двумя значениями, т.е. вместо устойчивого цикла с периодом, равным 1, соответствующего одной неподвижной точке, у системы имеется устойчивый цикл с периодом 2.

Значение параметра r, при котором единственная неподвижная точка х* расщепляется, или происходит бифуркация на два осциллирующих значения х₁* и x₂* равно r = 3/4. Пара величин (х₁* и х₂*) образует устойчивый аттрактор с периодом 2.

г. Опишите экологический сценарий популяции насекомых или человеческого общества, которые ведут себя аналогично отображению из п. «в».

д. Что является устойчивым аттрактором стандартного отображения (8.6) для значений параметра r = 0.863 и 0.88? Чему равен период в каждом случае?

е. Что является устойчивым аттрактором стандартного отображения и чему равны соответствующие периоды для значений параметра r = = 0.89, 0.891 и 0.8922?

ЗАДАЧА 8.2. Хаотический режим

а. Область значений параметра r > r_c = 0.892486417967... называется хаотическим режимом, в котором две близлежащие начальные точки разбегаются по различным траекториям после небольшого числа итераций. В качестве примера выберите такие источники x₀ = 0.500 и 0.501. Сколько итераций необходимо для того, чтобы последующие значения различались между собой более чем иа 10%?

б. Известно, что точность представления чисел с плавающей запятой в компьютере конечна. Для проверки влияния конечной точности вашего компьютера выберите сначала значения r = 0.91 и x₀ = 0.5 и получите численное значение х после приблизительно 200 итераций. Затем модифицируйте свою программу так, чтобы последовательно выполнялись операции х = x/10 и х = 10*х. Эта комбинация действий обрезает последнюю десятичную цифру, которую хранит компьютер. Получите итерированное значение х при тех же условиях и сравните результаты. Будет ли такое же несовпадение и в случае r < r_c?

в. Каковы динамические свойства системы для значения параметра r = 0.958. Можете ли вы найти другие «окна» в этом хаотическом режиме?

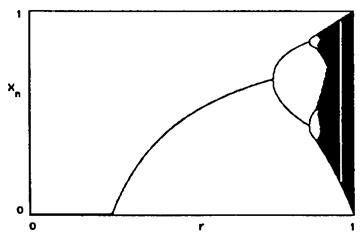
Рис. 8.2. График итерированных значений х в зависимости от параметра роста r. Обратите внимание на переход от периодического движения к хаотическому. Обратите также внимание на узкие окна периодического движения внутри областей хаоса.

Другой способ представить поведение (8.6) заключается в построении графика зависимости х от управляющего параметра r (рис. (8.2). На рис. 8.2 нанесены итерированные значения х, полученные только после завершения переходного периода.

ЗАДАЧА 8.3. Качественные особенности квадратичного отображения

а. Модифицируйте программу так, чтобы итерации х_п строились в виде графика, зависящего от r. Не нужно наносить на график первые n итераций. Начните с диапазона 0.8 < r < 0.9. Сколько удвоений периода вы можете различить?

б. Измените масштаб так, чтобы вы могли наблюдать итерации х от периода 4 до периода 32. Как выглядит график в этом масштабе по сравнению с графиком для отображения с периодом 4 в исходном масштабе?

в. Дайте краткое качественное описание поведения кривой вблизи точек бифуркации.

8.3. Удвоение периода

Приведенные выше «машинные эксперименты», касающиеся поведения стандартного отображения, привели к созданию нового словаря для описания наших наблюдений и, вероятно, убедили вас в том, что свойства простых динамических систем могут быть очень сложными!

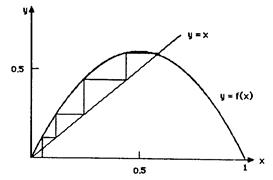
Рис. 8.3. Итерации отображения x_n+1 = 4rx_n(l – x_n) с r = 0.6 и начальным значением x₀ = 0.05. Неподвижная точка х = 0 –неустойчива, а неподвижная точка х = 0.58333 является устойчивой.

Для понимания зависимости динамического поведения от параметра r представим простой и элегантный графический метод итерирования f(x). На рис. 8.3 приведен график f(x) для значения параметра r = 0.6. Наклонная прямая, соответствующая функции у = х, пересекает кривую у = f(x) в двух неподвижных точках х* = 0 и х* = 0.58333, т.е. повторение итераций функции f(х) для значений х* = 0 и х* = 0.58333 дает постоянную последовательность. Если х₀ не является одной из неподвижных точек, мы можем найти орбиту следующим образом. Сначала проводим вертикальную прямую из точки {х = х₀, у = 0} до пересечения с кривой у = f(x) в точке {x₀, у₀ = f(x₀)}. Затем проводим горизонтальную прямую из точки {x₀, y₀} до пересечения с наклонной прямой в точке {y₀, y₀}. Поскольку на этой наклонной прямой значение у равно значению х, то значение х в точке пересечения является первой итерацией х₁ = у₀. Аналогично можно найти вторую итерацию x₂. Из точки {x₁, y₀} проводим вертикальную прямую до пересечения с кривой у = f(x). Фиксируем точку у = у₁ = f(x₁) и проводим горизонтальную прямую до пересечения с наклонной; значение х в точке пересечения дает х₂. Дальнейшие итерации можно найти, повторяя следующую процедуру:

1) двигаемся по вертикали до пересечения с кривой у = f(x);

2) двигаемся по горизонтали до пересечения с наклонной прямой у = x;

3) повторяем шаги 1 и 2 бесконечное число раз.

Этот графический метод иллюстрируется на рис. 8.3 для х₀ = 0.05 и r = 0.6. Заметим, что если начинать итерации из любой точки x0 (х ≠ 0 и х ≠ 1), то итерационный процесс будет сходиться к неподвижной точке x* = 7/12 ≈ 0.58333. (С помощью карандаша проверьте этот факт на рис. 8.3.) Такие неподвижные точки называются устойчивыми (аттрактор с периодом 1). По сравнению с этим независимо от близости x₀ к неподвижной точке х = 0 итерационный процесс будет расходиться. Такая неподвижная точка называется неустойчивой.

Как можно объяснить качественное различие между неподвижными точками x* = 0 и х* = 0.58333 для r = 0.6? Локальная кривизна кривой у = f(x) определяет горизонтальное смещение при каждой итерации f. Крутой наклон (более 45°) приводит к удалению x от начального значения. Следовательно, критерий устойчивости неподвижной точки заключается в том, что величина наклона в неподвижной точке должна быть менее 45⁰, т.е. если |df(x)/dx|_x=x* < 1, то точка х* является устойчивой, и, наоборот, если |df(x)/dx|_x=x* > 1, тогда точка х* неустойчива. Внимательное изучение функции f(x), изображенной на рис. 8.3, показывает, что x = 0 – неустойчивая точка, поскольку тангенс угла наклона кривой f(x) в точке x = 0 больше единицы. В противоположность этому значение производной f(x) в точке х = 0.58333 меньше единицы.

Таким образом, для значений 0 < r < 3/4 конечное поведение известно.

Что происходит, если r лежит в интервале 3/4 < r < 1? Нам известно из наблюдений, что по мере роста r неподвижная точка функции f становится неустойчивой и приводит к рождению (бифуркации) цикла с периодом 2. Теперь только после каждой второй итерации х принимает то же самое значение, т.е.

xi = f(f(xi)), i = 1, 2

(8.7)

и аттракторы функции f(x) являются неподвижными точками функции g(x) = f(f(x)). Что произойдет, если дальше увеличивать значение параметра r? В конце концов, величина наклона неподвижных точек g(x) достигнет единичного значения и неподвижные точки удвоятся. Теперь период f равен 4 и можно изучать устойчивость неподвижных точек четырежды итерированной функции h(x) = g(g(x)) = f(f(f(f(x)))). Эти неподвижные точки также в конце концов удваиваются и наблюдается явление удвоения периода, т.е. период 1 → период 2 → период 4 → период 8 → период 16 → период 32 → .... что мы и видели в задаче 8.4.

ЗАДАЧА 8.4. Качественные свойства неподвижных точек

а. Используйте программу зависимость x_n от r и покажите графически, что при r < 3/4 у функции f(x) существует единственная устойчивая неподвижная точка. Функция f(x) четна относительно точки х = 1/2, в которой f(x) имеет максимум. Каковы качественные особенности второй итерации этой функции g(x) = f(f(x)? Четна ли функция g(x) относительно точки x = 1/2? Является ли точка х* также неподвижной точкой функции g(x)? При каком значении х функция g(x) имеет минимум? Пусть r₁ – значение r, при котором неподвижная точка функции f(x) становится неустойчивой. Убедитесь в том, что r₁ = –0.75.

б. Охарактеризуйте орбиту функции f(x) для значения параметра г = 0.785. Чему равен период f(x)? Чему равны численные значения неустойчивых аттракторов? Проитерируйте g(x) и найдите две неподвижные точки х₁* и x₂* этого отображения. (Попробуйте два начальных значения х₀ = 0.1 и x₀ = 0.3.) Являются ли неподвижные точки отображения g(x) устойчивыми или неустойчивыми? Как соотносятся значения х₁* и x₂* со значениями неустойчивых аттракторов отображения f(x)? Убедитесь в том, что наклоны функции g(x) в точках х₁* и х₂* одинаковы.

в. Проверьте следующие свойства неподвижных точек отображения g(x). По мере увеличения параметра r неподвижные точки g(x) расходятся и наклон g(x) в неподвижных точках уменьшается. При каком значении r = r⁽¹⁾ одна из неподвижных точек g равна 1/2? Чему равно значение другой неподвижной точки? При этом значении параметра r наклон в обеих неподвижных точках равен нулю. При дальнейшем увеличении r наклоны в неподвижных точках становятся отрицательными. Наконец, при r = r₂ = 0.8623 наклоны в обеих неподвижных точках функции g(x) становятся равными –1 и эти две неподвижные точки превращаются в неустойчивые.

г. Покажите, что для значений r, чуть больших r₂, например r ≈ 0.87, у функции h(x) = g(g(x)) имеются четыре неподвижные точки. Чему равно значение r = r⁽²⁾, при котором одна из неподвижных точек равна 1/2? Чему равны значения трех остальных неподвижных точек при r = r⁽²⁾. При каком значении r = r₃ четыре неподвижные точки отображения h становятся неустойчивыми?