Метод касательных (метод Ньютона)

Белорусский национальный технический университет

Автотракторный факультет

Кафедра «Тракторы»

Группа 101019

Отчёт

По лабораторной работе №6

по курсу «Математическое моделирование»

«Численные методы решения алгебраических и трансцендентных уравнений»

Выполнил:

Проверил:

Минск 2011

Цель работы: знакомство с некоторыми, наиболее широко используемых при проектировании и исследовании узлов и агрегатов мобильных машин, методами решения уравнений.

Математическая модель:

Метод касательных (метод Ньютона)

Метод последовательных приближений, разработанный Ньютоном, широко используются для построения итерационных алгоритмов. Его популярность обусловлена тем, что для определения интервала, в котором заключен корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции в методе Ньютона осуществляется экстраполяция с помощью касательной к кривой в данной точке. На рисунке 1 показана блок-схема алгоритма этого метода, в основе которого лежит разложение функции 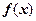в ряд Тейлора

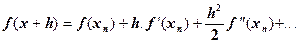
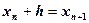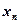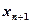Члены, содержащие h во второй и более высоких степенях, отбрасываются и используется соотношение . Предполагается, что переход от к приближает значение функции к нулю так, что 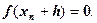Тогда

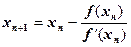
причем за нулевое приближение 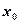принимается такое значение из отрезка [а, в], для которого выполняется условие .

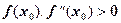Значение 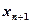соответствует точке, в которой касательная к кривой в точке 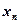пересекает ось x-ов. Так как кривая 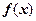отличная от прямой, то значение функции 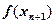скорее всего не будет равняться нулю. Поэтому вся процедура расчета повторяется, причем вместо 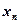используется 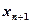. Счет прекращается по достижении условия 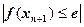. Здесь e - точность вычисления, задаваемая расчетчиком.

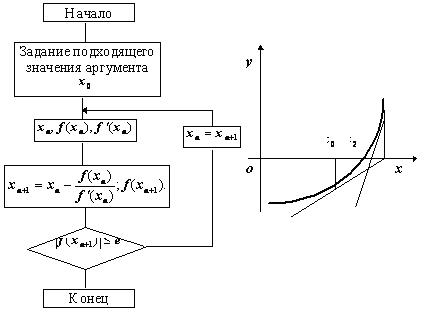
Рисунок 1- Графическая интерпретация метода касательных и блок-схема алгоритма метода касательных.

На рисунке 1 процесс решения уравнения методом касательных показан графически. Ясно видно, что быстрота сходимости в большой мере зависит от удачного выбора начальной точки.

Если в процессе итераций тангенс угла наклона касательной 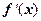обращается в нуль, то применение метода осложняется. В случае бесконечно большого значения 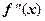метод также не будет эффективным. Так как условие кратности корней имеет вид 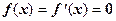, то в этом случае метод Ньютона не обеспечивает сходимости.

Подпрограммы МК уточнения корня уравнения методом касательных и FunMK, в которой описываются решаемое уравнение и производная, представлены на рисунке 2.

Procedure MK(x0,e:real;Var x:real); Procedure FunMK(x:real;Var fx,fx1:real);

Var z,fx,fx1 : real; Var y,y1,tg:real;

I : integer; begin

{$I FunMK} y:=0.55*x+0.1;

begin y1:=cos(y);

x:=x0; i:=1; tg:=sin(y)/y1;

repeat fx:=x*x-tg;

FunMK(x,fx,fx1); fx1:=2*x-0.55/sqr(y1)

z:=fx/fx1; end;

x:=x-z;

Inc(i); fx1:=abs(fx);

until (fx1<=e) or (i>50)

End;

Рисунок 2 - Тексты подпрограмм MK и FunMK

В подпрограмму МК передаются начальное значение аргумента 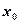и точность вычисления e. Вычисления продолжаются пока не выполнится условие 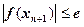или число итераций станет больше 50. Значение функции и производной вычисляются в подпрограмме FunMK, в которую передается значение аргумента x. Из подпрограммы FunMk в вызывающую подпрограмму MK возвращаются значения функции и производной.

Исходное уравнение: X⁴-14X³+60X²-70X=0

Текст программы:

begin

DecimalSeparator:='.';

Gran(a0,B,K,R1);

predel(R1,R2,x0);

MK(x0,e,x);

AssignFile(Fr,'Rez.dat');

Rewrite(Fr);

x1:=R2;

Repeat

x1:=x1+0.001;

rrr(x1,Fx);

writeln(Fr,' ', x1:6:4,' ', Fx:8:4,' ');

CloseFile(Fr);

end;

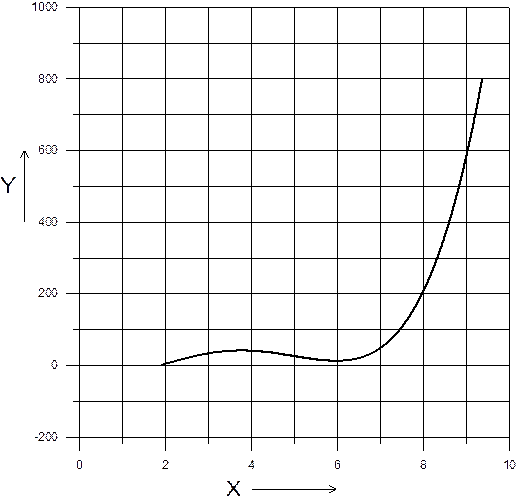
X_min=1,8666 X_max=9,3666

Вывод: В ходе работы познакомился с некоторыми, наиболее широко используемых при проектировании и исследовании узлов и агрегатов мобильных машин, методами решения уравнений. Нашел наибольший и наименьший корень уравнения методом касательных.