Методика определения ёмкости установки

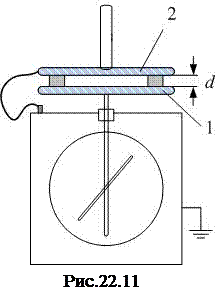Пластина 1 вместе с корпусом 5 образуют конденсатор ёмкостью С_УСТ., так как изолированы друг от друга. Ёмкость установки С_УСТ. Можно определить с помощью плоского конденсатора ёмкостью С_ПЛ., который получится, если на пластину 1 установки положить пластину 2 с изолирующими ножками высотой d (рис.22.11). Поскольку пластина 2 заземлена, то конденсаторы С_УСТ. и С_ПЛ. окажутся соединены параллельно (докажите это!), и общая ёмкость равна сумме ёмкостей:

.

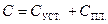Полный заряд системы установка – плоский конденсатор сохранится, тогда

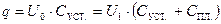, (22.12)

где U₀ – напряжение на установке без дополнительной пластины 2, U₁ – напряжение на установке после того, как на пластину 1 положили пластину 2. Из (22.12) получим расчётную формулу:

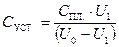. (22.13)

Методика определения ёмкости проводника (шара)

В комплект установки входят два металлических шара, ёмкости которых можно определить с помощью установки. Методика измерений такая же, как и при определении ёмкости установки: при соединении незаряженного шара и пластины 1 установки заряд её, сохраняясь, только перераспределяется между установкой и шаром.

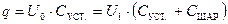. (22.14)

Здесь С_ШАР – ёмкость шара. Однако возникают две сложности.

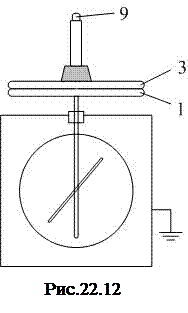1) Длина проводника должна быть такова, что на соответствующем расстоянии заряженные установка и шар не влияли друг на друга, то есть чтобы их взаимная ёмкость была бы ещё достаточно мала. В качестве такого проводника используется пластина 3 с металлическим стержнем 9 (рис.22.8 и 22.12). Длина стержня такова, что при меньшем расстоянии между шаром и установкой уже нельзя было бы пренебрегать взаимной ёмкостью шара и установки.

Таким образом, перед измерением ёмкости шара нужно на пластину 1 положить пластину 3 (рис.22.12). Однако при этом изменяется (увеличивается) ёмкость установки, и требуется снова её определить. При добавлении незаряженной пластины полный заряд сохраняется, поэтому

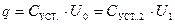, откуда

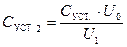, (22.15)

где где U₀ – напряжение на установке без дополнительной пластины 3, U₁ – напряжение на установке после того, как на пластину 1 положили разряженную пластину 3.

2) Ёмкость шара мала по сравнению с ёмкостью установки, поэтому разница в показаниях прибора до и после касания разряженным шаром заряженной установки невелика при однократном касании. Можно проделать процедуру несколько раз, каждый раз перед касанием шаром установки разряжая шар, тогда их (22.14) получим: 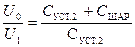после первого касания; 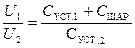после второго касания, что даст:

,

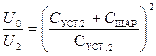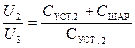после третьего касания; и тогда

,

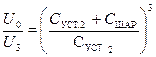и так далее. Окончательно получим после N касаний:

,

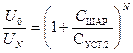или

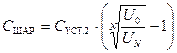. (22.16)

Порядок выполнения работы

Задание 1. Определение ёмкости установки

Для определения ёмкости установки необходимо:

1. Измерить диаметр D пластин установки.

2. Измерить высоту d ножек на пластине 2.

3. Рассчитать ёмкость С_ПЛ. плоского конденсатора по формуле (22.3):

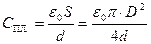. (22.3)

Все величины занести в табл. 22.1.

4. Снять пластину 2 с пластины 1 установки и поместить её на заземлённые опоры 3.

5. Зарядить установку. Для этого:

а) Потереть линейку бумагой (или тряпочкой из целлюлозного волокна);

б) положить линейку на пластину 1 установки;

в) прикоснуться рукой к пластине, снимая с неё индуцированный заряд;

г) убрать линейку.

Стрелка электрометра при этом должна отклониться примерно на 60÷70 делений.

6. Занести в таблицу 22.1 угол отклонения стрелки электрометра α₀. Используя градуировочную таблицу 22.4, определить соответствующее углу α₀ напряжение U₀.

7. Положить на пластину установки заземлённую пластину 2.

8. Записать новое значение угла отклонения электрометра α₁ и определить напряжение U₁.

9. Убрать пластину 2, снова подзарядить установку (пункт 5) и повторить пункты 6-8. Повторить измерения α₀ и соответствующих им α₁ 3 раза.

10. По формуле (22.13)

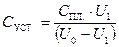(22.13)

вычислить ёмкость установки С_УСТ., рассчитать среднее значение.

Таблица 22.1.

№	D, м	d, м	СПЛ, пФ	α0, дел.	U0, В	α1, дел.	U1, В	СУСТ, пФ
Среднее:

Задание 2. Определение ёмкости установки с пластиной 3

Для определения ёмкости С_УСТ.2 нужно:

1. Зарядить установку, как описано в пункте 5 предыдущего задания.

2. Записать угол отклонения стрелки прибора α₀ в таблицу 22.2.

3. Разрядить пластину 3, прикоснувшись ею о зачищенные «рёбра» 10 (рис.22.8) заземлённого корпуса установки. При этом держать пластину 3 за изолированную часть стержня.

4. Положить пластину 3 на пластину 1 установки (рис.22.12). Записать угол α₁ отклонения стрелки прибора.

Таблица 22.2.

№	α0, дел.	U0, В	α1, дел.	U1, В	СУСТ.2, пФ
Среднее:

5. Убрать пластину 3, снова подзарядить установку и повторить пункты 2-4. Повторить измерения α₀ и соответствующих им α₁ 3 раза.

6. По градуировочной таблице 22.4 определить соответствующие углам α напряжения U.

7. По формуле (22.15) рассчитать ёмкость установки С_УСТ.2 в каждом опыте, рассчитать среднее значение С_УСТ.2.

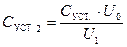. (22.15)

8. Все данные занести в таблицу 22.2.

Задание 3. Определении ёмкости шара

Для определения ёмкости шара необходимо:

1. Положить на пластину 1 установки пластину 3 с закреплённым на ней металлическим стержнем (рис.22.12).

2. Зарядить установку вместе с пластиной 3, как описано в п. 5 задания 1. Записать в табл.22.3 угол α₀.

3. Взять большой шар за диэлектрическую ручку.

4. Снять с шара заряд, прикоснувшись им к зачищенным «рёбрам» 10 (рис.22.8) заземлённого корпуса установки.

5. Прикоснуться шаром к концу 9 металлического стержня пластины 3.

6. Повторить пункты 4 и 5 N раз (N=8÷16). Внимательно считать число касаний! Записать N и угол α_N.

7. По градуировочной таблице определить напряжения U₀ и U_N, соответствующие углам α₀ и α_N.

8. По формуле (22.16) вычислить экспериментальное значение ёмкости шара:

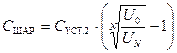. (22.16)

9. Повторить эксперимент ещё 2 раза (пункты 2-8).

10. Найти среднее значение С_ШАР.

11. Измерить радиус шара R. Рассчитать теоретическое значение С_ШАР.Т. по формуле (22.17) и сравнить с экспериментальным.

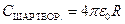. (22.17)

12. Результаты измерений и вычислений занести в табл.22.3.

Таблица 22.3. Большой шар

№ п/п	α0, дел.	U0, В	N	αN,дел.	UN, В	СШАР, пФ	R, м	СШАР.ТЕОР., пФ
Среднее:

13. Повторить измерения и вычисления по пунктам 2÷12 для меньшего шара.

14. Все результаты занести в табл.22.4.

Таблица 22.4. Малый шар

№ п/п	α0, дел.	U0, В	N	αN,дел.	UN, В	СШАР, пФ	R, м	СШАР.ТЕОР., пФ
Среднее:

Задание 3. Определение ёмкости цилиндрического конденсатора и диэлектрической проницаемости изоляции коаксиального кабеля

Для выполнения задания нужно:

1. Положить на пластину 1 установки заземлённую пластину 2.

2. Зарядить установку вместе с пластиной 2, как описано в п. 5 задания 1, положив заряженную линейку между обкладками получившегося плоского конденсатора на пластину 1.

3. Записать в табл.22.5 угол α₀.

4. Разрядить цилиндрический конденсатор, роль которого играет кусок коаксиального кабеля 13 (рис.22.13). Для этого обоими оголёнными проводами 12 кабеля одновременно прикоснуться к заземлённому электроду 11 (22.13,а), не касаясь пластины 1.

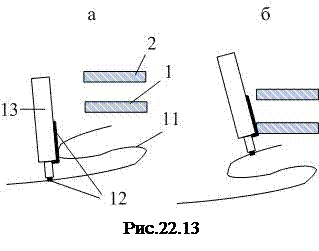5. Прикоснуться оголёнными проводами кабеля одновременно к заземлённому электроду 11 и нижней пластине 1 плоского конденсатора (рис.22.13,б).

6. Записать в табл.22.5 угол α₁.

7. Определить напряжения U₀ и U₁, соответствующие углам α₀ и α₁.

8. Повторить опыт ещё 2 раза (пункты 3÷7). Если нужно, подзаряжать установку (см. пункт 5 задания 1).

9. Рассчитать в каждом опыте экспериментальное значение ёмкости цилиндрического конденсатора по формуле (22.18):

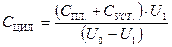. (22.18)

10. Рассчитать среднее значение С_ЦИЛ..

11. Измерить длину l коаксиального кабеля.

12. Используя (22.6), рассчитать диэлектрическую проницаемость ε изоляции кабеля.

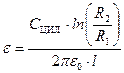, (22.6)

где радиус внутренней жилки R₁=0 .5 мм, радиус внешней оплётки R₂=2.5 мм.

12. Результаты всех измерений и вычислений занести в табл.22.5.

Таблица 22.5

№	α0, дел.	U0, В	α1, дел.	U1, В	СЦИЛ, пФ	R1, мм	R2, мм	l, м	ε
						0.5	2.5
Средние:

13. Сде­лайте вы­во­ды.

Контрольные вопросы

1. Что называется емкостью проводника? Конденсатора?

2. Выведите формулу для емкости плоского конденсатора; сферического конденсатора; цилиндрического конденсатора.

3. Что такое электростатическая индукция?

4. Как можно зарядить электрометр?

5. Опишите методику определения ёмкости установки; проводника; цилиндрического конденсатора.

6. Выведите формулу для ёмкости изолированного шара.

Таблица 22.6.

Зависимость напряжения от угла отклонения стрелки электрометра

α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5

Используемая литература

[1] §§ 16.1-16.3;

[2] §§ 11.5, 11.6;

[3] §§ 2.15-2.18, 2.20, 2.22;

[4] т.2, §§ 26, 27;

[5] § 94.

Библиографический список

1. Детлаф, А.А. Курс физики/ А.А. Детлаф, Б.М. Яворский.-М.: Высш.шк., 1989.-500 с.

2. Калашников, Н.П. Основы физики: учебник для вузов: в 2-х т. / Н.П. Калашников, М.А. Смондырев. – 2-е изд., перераб. – М.: Дрофа, 2003. Т.1. - 400 с. Т.2. – 432 с.

3. Лозовский, В.Н. Курс физики: учебник для вузов: в 2-х т./ Под ред. В.Н. Лозовского. – СПб.: Лань, 2000.-Т.1-676с.; Т.2.-592с.

4. Савельев, И.В., Курс общей физики: учеб. пособие: в 3-х т. / И.В. Савельев.- 5-е изд., стер. – СПб.: Лань, 2006.

5. Трофимова, Т.И. Курс физики / Т.И. Трофимова. – М.:Высш. школа, 1999. - 542 с.