Мора кернеуінің диаграммасы 1 страница

О. Мора бойынша кернеу диаграммасы (немесе Мор шеңберлері) нормальды қысым -р және жанама τ кернеулер векторлары жиынтығы туралы түсінікті графикалық түрде береді. Бұл кернеулер бас осьтер жүйесінде қаралатын әр түрлі көлбеген алаңдарда әсер етеді. Нормальды қысым -р мөлшерін абсцисса осі бойымен салып, ал оның әрбір мөлшеріне сәйкес келетін жанама кернеулерді τ ордината осі бойымен салып диаграмманы тұрғызады.

Көлбеген алаңдағы нормальды қысым мынандай формуламен анықталатындығы белгілі [(6.3)формуласы]: .

Осымен бірге (6.5) және (6.3) теңдеулерінен мынау келіп шығады:

. (6.11)

Бұдан басқа, бағыттаушы косинустар үшін мынандай түрде болатын белгілі шартты жазайық: (6.12)

(6.3) теңдеуінің екі жағында көбейтейік. Содан кейін алынған нәтижені мүшелеп (6.11) теңдеуінен алып тастайық. Ары қарай, (6.12) теңдеуінің екі жағында алдын ала көбейтіп жоғарыда алынған теңдеуге қоссақ мынандай формуланы аламыз:

(6.13)

(6.13) теңдеуінің екі жағынада қосып және қарапайым түрлендіруден кейін мынаны аламыз: (6.14)

Осы әдістемені қолданып жоғарыдағы ұқсас тағы да екі теңдеуді шығарамыз. Бұл мынандай теңдеулер:

(6.15)

(6.16)

Алынған (6.14), (6.15) және (6.16) теңдеулерін аналитикалық геометриядан белгілі мынандай шеңбер теңдеуімен салыстырсақ: осы теңдеулерде шеңберді анықтайды деген қорытындыны шығара аламыз. Осы шеңберлердің центрі абцисса осі бойымен орналасады және (6.14), (6.15) және (6.16) теңдеулері үшін сәйкесті мынандай ара қашықтықта тұрады: және

Шеңбер радиусының R еке есе дәрежесі болып саналатын (6.14), (6.15) және (6.16) теңдеулерінің оң жақтарында өзгеретін параметр , және бар. Сондықтан (6.14), (6.15) және (6.16) теңдеулерінің әрбіреуі тұқымдас шоғырланған шеңберлердің теңдеулері болып саналады.

(6.3), (6.11) және (6.12) теңдеулері берілген жағдай үшін және τ кернеулерінің қатнастық мәндерін анықтайды. Осы теңдеулерді (6.14), (6.15) және (6.16) теңдеулер жүйесіне математикалық түрлендірген кезде физикалық мәндері өзгертмейтін болады.

Сөйтіп (6.14) теңдеуі бағыттаушы косинусының әр түрлі берілген мәндері үшін және τ нүктелерінің геометриялық орнын шеңбер түрінде анықтайды. Осы (6.15) және (6.16) теңдеулеріне де әділ.

Демек , және бағыттаушы косинустардың берілген мүмкін болатын топ мәндеріне (яғни (6.12) шартын қанағаттандыратын) және τ мөлшерлері үш шеңберлердің қилысатын нүктесімен анықталады (6.2 сурет).

Ары қарай қандай аймақта осы нүктелер орналасуы мүмкін екендігін анықтайық. Анықтау үшін шартын қабылдайық, яғни 1 көрсеткішімен мөлшері бойынша ең үлкен басты нормальды кернеуді, 3 көрсеткішімен ең кіші басты нормальды кернеуді, ал 2 көрсеткішімен аралық басты нормальды кернеуді белгілейік. Осы шартты ылғида сақтауға болады.

Бағыттаушы косинустардың мынандай сәйкесті мәндері үшін: және яғни бұрышы үшін (6.14), (6.15) және (6.16) теңдеулерімен берілген шеңберлердің R₁, R₂ және R₃ радиустер мөлшелерін анықтайық. Осы радиустер мынаған тең:

(6.17)

6.2 – сурет. Мор шеңберлері

(6.14) және (6.16) теңдеулерінен көрініп тұрғандай және мөлшерлерін үлкейткен кезде сәйкесті шеңберлердің радиустері үлкейеді. және τ кернеулерінің мүмкін болатын жұп мәндері және радиусы бар шеңберлердің үстінде немесе оның сыртында, бірақта ішінде орналасуы мүмкін еместігін осы білдіреді.

Егер мөлшері үлкейетін болса, онда R₂ радиусы кішірейеді. Өйткені жоғарыда қабылданған басты кернеулердің қатнастарына сәйкесті айырымы теріс мәнді алады. Демек және τ мөлшелері болған кезде R₂ радиусы бар шеңбердің ішінде орналасады.

, және радиустары бар шеңберлерді жоғарыда көрсетілген центрлерден (6.17)) теңдеулерін қолданып салып Мора диаграммасын аламыз (6.3 сурет). Бір-біріне сәйкес келетін және τ кернеулерінің қос мөлшерлері сызықтап тастаған қисық сызықты үшбұрыштың ішінде жатады. 6.3 суретте тағы да диаграмманың ерекше нүктелері көрсетілген.

Шеңберлер радиусы басты жанама кернеулердің мөлшерлеріне саны бойынша тең екендігі (6.17) теңдеулерінен көрініп тұр.

6.4 – сурет. Мор диаграммасы

Берілген бұрыштар , және бойынша 6.4 сурет көрсетілген тұрғызулардың көмегімен көлбеген алаңдағы және τ мәндерін анықтауға және кері есептерді шешуге болады. Жалпы жағдайға Мора диаграммасы бойынша жанама кернеудің таңбасын анықтай аламыз.

, және кернеулерін бірдей мөлшерге үлкейткен де немесе кішірейткен де басты шеңберлердің радиустары және центрлері арасындағы ара қашықтық өзгермейтіндігін оңай көруге болады. Осындай жағдайда τ осінің жайы ғана өзгереді. Егер τ осін орташа нормальды кернеудің мөлшеріне фигура жаққа жылжытсақ (6.4 суретте көрсетілген жағдайда оңға қарай жылжыту), онда кернеу девиаторының бейнесін аламыз (6.5 сурет). Бұндай жағдайға τ осі ылғида фигураны кесіп өтеді. Осы осьті 6.5 суретте көрсетілген тұрғызулардың көмегімен есептемей жүргізуге болады.

6.4 – сурет. Мор диаграммасы

6.5 – сурет. Мор диаграммасы

Кернеудің шарлық тензоры координаттың басынан ара қашықтығында орналасқан радиусы нөльге тең шеңбермен ( нүктесімен) Мор диаграммасында бейнелейді.

Негізгі әдебиеттер: [1] (тарау 4, бет 101 – 109); [2] (тарау 3, бет 77 – 101); [3] (тарау 1, бет 16 – 75); [4] (тарау 2, бет 70 – 105).

Қосымша әдебиеттер: [6] (тарау 2, бет 21 – 30).

Бақылау сұрақтары:

1. Ең үлкен жанама кернеулердің алаңдары басты осьтерге қатысты қалай бағдарланған?

2. Мор диаграммасын не үшін қолданады?

3. Мор диаграммасының диаметрін қалай анықтайды?

4. Мор диаграммасының центрін қалай табады?

5. Ең үлкен жанама кернеулер әсер ететін алаңның бағыттаушы косинустары неге тең?

6. Ең үлкен жанама кернеулер қалай анықталады ?

7. Мор диаграммасын қандай әдістемені қолданып тұрғызады ?

№7 дәріс. Лагранж және Эйлер айнымалы шамалары.

Нүкте және бөлшектер. Тұтас ортада жүретін процестерді зерттегенде нүкте деген термин қолданалады. Бұл терминді екі мағанада қолдануға болады. Біріншісі бақлаушының қозғалмайтын кеңістігінің белгіленген нүктесі ретінде қарау. Екіншісі осы кеңістіктегі тұтас ортаның қозғалатын материальды нүктесі ретінде қарау. Сондықтан ары қарай нүкте термині кеңістіктің белгіленген нүктесін білдіретін болады. Тұтас ортаның материальды нүктелерін бөлшек деп атайтын боламыз.

Сызық, бет немесе көлем сияқты геометриялық объектілерді қарағанда және бұл сөздерге кеңістіктік немесе материальдық деген сөздерді қосқанда (мысалы, кеңістіктік бет, материальдық көлем және тағы басқалар) осы фигуралар сәйкесті нүктелерден немесе бөлшектерден құралған деп есептейтін боламыз. Қарап отырған уақыт мезгелінде, байқаушының кеңістігіндегі кейбір D аймақты толтыратын шексіз көп материальды бөлшектер денені құрайды. Денені құрайтын бөлшектердің орналасуы, яғни оның құрама пішіні уақыт өткен сайын жалпы жағдайға өзгереді.

Лагранж айнамалы шамасы. Тұтас ортаның қозғалысын зерттеген кезде тағы да екі түрлі көзқарас пайда болды.

Бірінші көзқарас Лагранж есімімен байланысты. Осы көзқарас бойынша зерттеу объектісі болып материальды бөлшектердің өздері саналады. Сонда тығыздық, температура, белгіленген материальды бөлшектің жылдамдығы сияқты кейбір скалярлық немесе векторлық мөлшерлердің уақытпен өзгеруі және тағыда осы мөлшерлердің бір бөлшектен екіншісіне өткен кезде өзгеруі қаралады.

Басқаша айтқанда осы мөлшерлер уақыттан және аланған бөлшектің даралылығын сипаттайтын айнымалылардан функция ретінде қаралады.

Осындай айнамалылар ретінде, мысалы 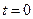болатын бастапқы уақыт мезгіліндегі еркін материальды бөлшектің декарттық координатасы –ді қабылдауға болады (7.1 сурет). Онда оның ағымдағы координатасы 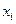, байқаушының қозғалмайтын кеңістігіндегі сол базисте, уақыт –ның және жоғарыда айтылған бөлшектің бастапқы координатасының мынандай функциясы болады: ; немесе қысқартылған түрде

. (7.1)

Сөйтіп бастапқы координаталарын белгілеп және уақыт –ны айнамалы деп есептеп біз бір белгіленген бөлшектің қозғалу заңын аламыз. –ді айнамалы деп санап және –ны белгілеп (7.1) формуласы бойынша берілген уақыт мезгіліенде кеңістікте материальды бөлшектің таралуын табуға болады.

7.1 – сурет. Материальды бөлшектің декарттық координат жүйесінде қозғалуы

Егер және –ны айнамалы деп саналса, онда (7.1) формулалары тұтас ортаның қозғалу заңы болып саналады. Әдеттегідей, соңында функциялары үздіксіз және барлық аргументтері бойынша үздіксіз жеке туындылары бар деп есептейтін боламыз, ал кез келген 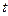уақыттарында (7.1) қатнасы өзара бір қатарлы болып келетіндігін ескеруіміз қажет.

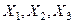айнымалары және 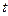уақыты Лагранж айнамалылары деп аталады. Материальды бөлшек жылдамдығы мен үдеу проекцияларын келесі формулалармен анықтайды:

(7.2)

Жалпы жағдайда қаралатын материальды көлемде бір бөлшекті екінші бөлшектен айыратын 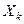декарттық координаттардың орнына осы бөлшектің бастапқы уақыт мезгілендегі ( 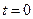) қисық сызықты координатасын –ді қолдануға болатындығын ескерте кету қажет.

Ілеспелі координаттар жүйесі. Осыған дейін тұтас ортаның қозғалысын біз байқаушының есеп беру жүйесіне қатысты қарадық, яғни қозғалмайтын тікбұрышты декарттық координат жүйесі 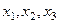қатысты қарадық. Бірақта (7.1) байланыстары бөлшектің кеңістіктегі жайын, оның 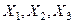лагранждық координатасымен толық анықтайтығын оңай көруге болады. Осы ілеспелі жүйе деп аталатын қозғалмалы деформацияланатын координаттар жүйесін 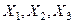, яғни тағыда бір есеп беру жүйесін еңгізуге мүмкіндік береді.

Бастапқы уақыт мезгілінде ілеспелі жүйенің материальды координатты сызықтары түзу болады. Кез келген келесі уақыт мезгілінде осы ілеспелі жүйенің материальды координатты сызықтары тұтас ортаның бөлшектерімен бірге, осы жүйенің координатты сызықтарына қайтадан ауысады, бірақта жалпы жағдайда кисайып кетеді. Ілеспелі қисық сызықты координат жүйесі тұтас ортаға бектілген және осы ортамен бірге деформацияланады деп айтуға болады (7.2 сурет).

Эйлер айнамалы шамасы. Эйлер есімімен байланысты екінші пікір бойынша, зерттеу объектісі болып қозғалмайтын бақылаушы кеңістігі қабылданады немесе қозғалатын ортамен толтырылған оның белгіленген бөлігі қабылданады. Қозғалысты сипаттайтын әр түрлі мөлшерлер нүкте және уақыт функциясы болып саналады, яғни Эйлер айнымалы шамасы деп аталатын үш аргумент 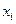және уақыт 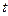–ның функциясы болады.

Мысалы, 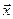радиус-векторы бар кеңістіктің берілген нүктесіндегі жылдамдық үшін формула мынандай түрді алады: .

Сөйтіп, Эйлердің ойы бойынша, зерттеу объектісі болып әр түрлі өрістер (скалярлық, векторлық немесе тензорлық) есептеледі. Осы өрістер тұтас ортаның қозғалысын сипаттайды.

7.2 – сурет. Көлем элементінің деформациясы

Эйлерлік айнымалы шамалардан Лагранждық айнымалы шамаларға ауысу. Сонымен Лагранждың көзқарасы бойынша біздің назарымызға жеке бөлшек жылдамдығының, қысымының, температурасының және басқа мөлшерлерінің өзгеру заңдары түседі. Ал Эйлердің көзқарасы бойынша біздің назарымызға кеңістіктің берілген нүктесінде осы шамалардың өзгеру заңдары түседі. Лагранж айнымалы шамасынан Эйлер айнымалы шамасына қалай өтуге болады? Осы сұраққа жауап беру үшін (7.1) байланысына сүйенейік. Айтылған байланысты 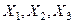қатысты шешіп мынаны аламыз:

, (7.3)

яғни Эйлер айнымалы шамасына ауысамыз. Егер координатасы 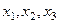болатын нүктені белгілесек, онда (7.3) формуласы қандай жеке бөлшектер 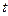уақтысында белгіленген кеңістік нүктесіне келетіндігін көрсетеді. (7.3) теңдеуін қатысты шеше отырып (7.1) теңдеуін аламыз, яғни Эйлер айнымалы шамаларынан Лагранж айнымалы шамаларына өтеміз.

Осындай ауысудың тағы да бір тәсілін қарайық. 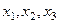координатасы және уақыт 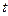–дан функция ретінде жылдамдық векторының сыңарлары бізге берілсін. Тұтас ортаның бөлшектерін дараландыратын 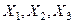параметрлері тұрақты болған кезде, сәйкесті координаттың уақыт бойынша туындысы қылып жылдамдық сыңарларын анықтайтын дифференциальдік теңдеулер жүйесін жазайық. Осы жүйені шешіп және 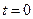, шартынан интегралдау тұрақтысын анықтап іздеген (7.1) байланысын табамыз.

Лагранждық және Эйлерлік түрде қозғалысты жазу. Бастапқы кезде ығысу кішкентай деген талапты қоймай тұтас ортаның қозғалысын қарайық. базисін таңдайық. Осы базисті байқаушымен салыстырғанда бектілген деп есептейміз.

Материальды бөлшек бастапқы 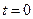уақтысында бастапқы координатасы ( 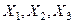) болатын кеңістік нүктесінде, ал ағымдағы 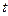уақтыснда ағымдығы координатасы ( 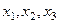) болатын кеңістік нүктесінде орналассын.

Сәйкесті радиус-векторларды мынандай түрде жазуға болады:

(7.4)

және . (7.5)

Сонымен бірге мынандай теңдікті де жазу әділ болады: , (7.6)

мұндағы 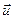– орын ауыстыру векторы.

Жоғарыда біз айтқанымыздай, тұтас ортаның қозғалысын бейнелейтін бастапқы және ағымды координаттардың арасындағы байланысты екі түрлі әдіспен көрсетуге болады.

Бірінші Логранждық әдісте тәуелсіз айнымалы шамалар болып бөлшектің бастапқы координатасы және уақыт 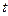есептеледі, демек немесе векторлық түрде

. (7.7)

Әдеттегідей осы сәйкестік өзара бір қатарлы деп жорамалдаймыз және де, (7.1) функцияларында кез келген ретті үздіксіз жеке туындылар бар болады деп есептейміз.

Осымен бірге тұтас ортаның қозғалысын мынандай қатнас түрімен жазуға болады:

немесе . (7.8)

Мұнда тәуелсіз айнымалы шамалар болып 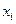координаталары және уақыт 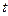саналады. Қозғалысты Эйлерлік әдіспен жазу ағымдағы уақыт мезгілінде ( 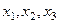) жайын алатын бөлшектің бастапқы координатасын табуға мүмкіндік береді.