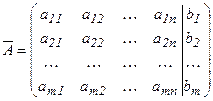Дәріс. Сызықтық алгебралық теңдеулер жүйесі. Матрицаның рангі

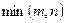А матрицасының рангі деп осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады және оны , немесе деп белгілейді. болады, мұндағы - m және n сандарының кішісі.

1-мысал. 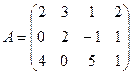матрицасының рангін табыңыз.

1-әдіс. Минорлар әдісі. Бұл матрицаның рангі 3-тен аспайды. Сондықтан 3-ші ретті минорлар құрамыз. Егер 3-ші ретті минорлардың ішінде бір нөлге тең емес минор табылса, онда ранг 3-ке тең болады. Ал 3-ші ретті минорлардың бәрі нөлге тең болса, онда минор 2-ге не 1-ге тең болады. Оны білу үшін тағы 2-ші ретті минорлар құрамыз. Олардың ішінде бір нөлге тең емес минор табылса, онда ранг 2-ге тең болады. Ал 2-ші ретті минорлардың бәрі нөлге тең болса, минор 1-ге тең.

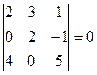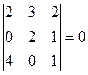, , 3-ші ретті минорлардың бәрі нөлге тең. Олай болса, 2-ші ретті минорлар құрамыз: 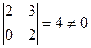. Демек ранг 2-ге тең, яғни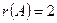

2-әдіс. Элементар түрлендіру әдісі. Матрицаны элементар түрлендіру деп:

1. матрицаның екі жолын (бағанын) ауыстыру;

2. матрицаның жолын (бағанын) нөлге тең емес санға көбейту;

3. бір жол (баған) элементтеріне басқа жолдың (бағанның) сәйкес қандай да бір санға көбейтілген элементтерін қосу амалдарын айтады.

Элементар түрлендіру арқылы алынған матрицаны бастапқы матрицаға эквивалентті матрица дейді және орталарына ~ белгісі қойылады. Матрицаның рангін табу үшін элементар түрлендіруді пайдаланып, матрицаны сатылы түрге келтіреміз.

Теорема. Матрицаны элементар түрлендіргеннен оның рангі өзгермейді.

2-мысал. 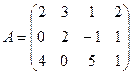~ ~ 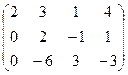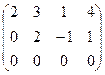. Демек ранг 2-ге тең, яғни .

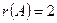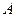Кері матрица.Егер шарты орындалса, онда матрицасын матрицасына кері матрица дейді және оны түрінде белгілейді. Мұндағы 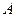, , 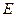матрицалары бірдей өлшемді квадрат матрицалар.

Ескерту: Егер 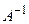матрицасы бар болса, онда ол жалғыз болады.

Теорема. КвадратА матрицасына кері матрица табылуы үшін 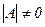болуы қажетті және жеткілікті. 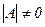болғанда кері матрица былайша есептелінеді .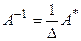

Мұндағы 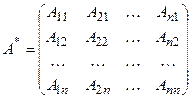алгебралық толықтауыштардан түзілген матрица.

3-мысал. 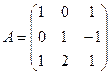матрицасына кері матрица табыңыз. .

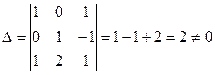Олай болса,

, , , , , , , ,

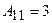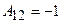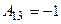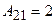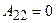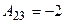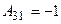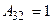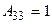
Сонда кері матрица былай болады: = .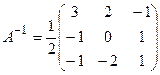

Сызықтық алгебралық теңдеулер жүйесі.n белгісізі бар m теңдеулер жүйесі былай жазылады:

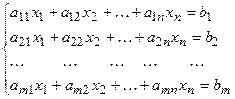
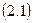
мұндағы 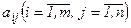жүйенің коэффициенттері, ал 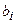- бос мүшелер деп аталады. 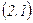жүйені матрицалық түрде былай жазуға болады 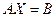немесе

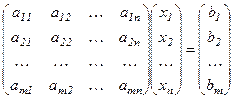, мұндағы А= 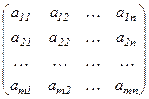жүйе матрицасы

A X B

деп аталады.

Егер 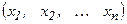сандар жиыны 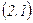теңдеулер жүйесін тепе-теңдікке айналдырса, онда бұл сандар жиыны осы жүйенің шешімі деп аталады.

Егер теңдеулер жүйесінің кемінде бір шешімі бар болса, онда жүйе үйлесімді деп аталады, ал жүйенің бір де шешімі болмаса, онда жүйе үйлесімсіздеп аталады.

Егер А матрицасын бос мүшелерден тұратын бағанмен толықтырса, онда пайда болған матрицаны кеңейтілген матрица дейді және оны 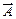деп белгілейді. Сонымен