Основные теоретические положения. Метод наложения основан на применении принципа наложения, который формулируется следующим образом:
Метод наложения основан на применении принципа наложения, который формулируется следующим образом:
Ток в любой ветви электрической цепи равен сумме токов, обусловленных действием каждого источника в отдельности, при отсутствии других источников.
Рассматриваемый принцип называют принципом независимого действия.
При действии только одного из источников напряжения предполагается, что Э.Д.С. всех остальных источников равны нулю, так же как равны нулю и токи всех источников тока. Отсутствие напряжения на зажимах источников напряжения равносильно короткому замыканию их зажимов. Отсутствие тока в ветви с источником тока равносильно разрыву этой ветви.
Если источник Э.Д.С. содержит внутреннее сопротивление, то, полагая Э.Д.С. равной нулю, следует оставлять в ветви его внутреннее сопротивление. Аналогично в случае источника тока с параллельной внутренней проводимостью, следует, разрывая ветвь источника (т.е. полагая 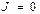 ), оставлять включенной параллельную ветвь с внутренним сопротивлением.
), оставлять включенной параллельную ветвь с внутренним сопротивлением.
Пусть в цепи действуют источники с параметрами 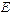 и
и 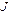 , тогда
, тогда 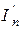 и
и 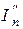 – токи n–ой ветви, создаваемые каждым из этих источников в отдельности.
– токи n–ой ветви, создаваемые каждым из этих источников в отдельности.
Согласно принципу наложения искомый тока:
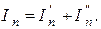
Принцип суперпозиции применим к напряжениям, т.к. между током и напряжением рассматривается линейная зависимость (закон Ома); но не применим к мощности: 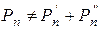
т.к. мощность – это квадратичные функции токов.
Примеры расчета линейных электрических цепей методом наложения
Пример 2.1
Дано: 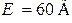

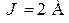

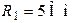

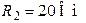

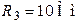

 .
.
Определить все токи методом наложения в схеме рис. 2.1.
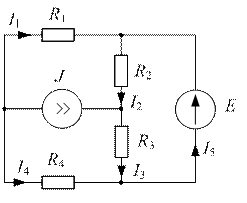 |  |
| Рис. 2.1 | Рис. 2.2 |
Решение
1) Заменяем источник Э.Д.С. E короткозамкнутым участком (т.к. его 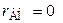 ) (схема рис. 2.2).
) (схема рис. 2.2).
Т.к. конфигурация цепи изменилась, то в цепи рис. 2.2 протекают токи, отличные от токов цепи рис. 2.1. Их называют первыми частичными токами и обозначают одним штрихом. Схему цепи рис. 2.2 более наглядно представим на рис. 2.3. Токи рассчитаем, применяя правило плеч и первый закон Кирхгофа:
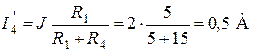 ;
;
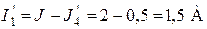 ;
;
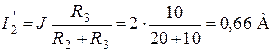 ;
;
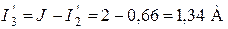 ;
;
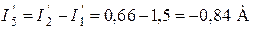 .
.
Ток 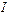 протекает по короткозамкнутому участку (его сопротивление равно нулю).
протекает по короткозамкнутому участку (его сопротивление равно нулю).
Запомнить! Ток в ветви, сопротивление которой равно нулю, определяют по первому закону Кирхгофа.
2) Разорвем ветвь с источником тока J. Токи, протекающие в цепи рис. 2.4, называют вторыми частичными токами и обозначают двумя штрихами.
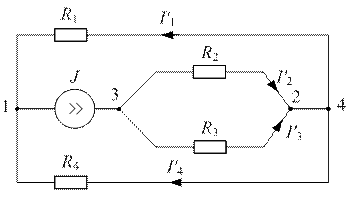 | 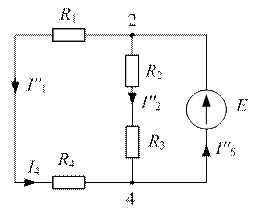 |
| Рис. 2.3 | Рис. 2.4 |
Напряжение, создаваемое Э.Д.С. E, приложено к двум параллельным ветвям. Токи 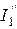 и
и 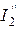 определим по закону Ома:
определим по закону Ома:
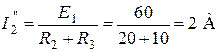 ;
;
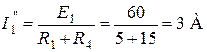 ;
;
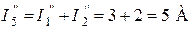 .
.
3) Искомые токи найдем как алгебраическую (т.е. с учетом направлений) сумму частичных токов:
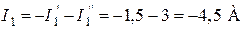 ;
;
 ;
;
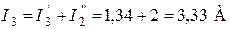 ;
;
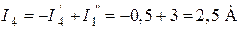 ;
;
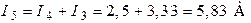 .
.
Ответ: 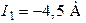 ,
, 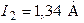 ,
, 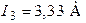 ,
, 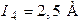 ,
, 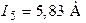 .
.
Метод контурных токов
