Поле потенциала. Градиент потенциала

Г.М. Казаков

Тепломассообмен

Утверждено редакционно-издательским

советом университета в качестве

учебного пособия

Нижний Новгород - 2016

ББК 31.31

К 14

Казаков Г.М. Тепломассообмен: Учебное пособие. – Н.Новгород: Нижегород. гос. архит.-строит. ун-т, 2016. – 93 с.

ISBN 5-87941-412-4

В пособии дан теоретический подход к решению широкого круга задач тепломассообмена: перенос теплоты через однослойные и многослойные стенки различной геометрической формы, теория подобия процессов и явлений, определение коэффициентов теплоотдачи при конвективном теплообмене. Подробно рассмотрены вопросы тепломассообмена при фазовых превращениях. В пособии показаны особенности лучистого теплообмена между твердыми телами, излучение и поглощение чистых газов и пламени, а также рассмотрены инженерные методы расчета теплообменных аппаратов.

Пособие может быть полезно для преподавателей и студентов теплоэнергетических специальностей.

ББК 31.31

ISBN 5-87941-412-4

© Казаков Г.М., 2016

© ННГАСУ, 2016

Введение

Теория переноса теплоты и массы вещества является одним из важнейших разделов современной науки. Она имеет большое практическое значение в самых разнообразных областях техники: в станционной и промышленной энергетике, технологических процессах химической и металлургической промышленности, строительной индустрии и коммунальном хозяйстве. Особенно большое значение проблема тепломассообмена имеет для новых областей техники, в частности, для ядерной энергетики и космической техники. Научной основой многих теплоэнергетических, энерготехнологических и химико-технологических процессов является теория тепломассообмена. Она включает в себя комплекс научных знаний из гидродинамики сплошных сред, молекулярной физики, термодинамики, уравнений математической физики, физико-химических поверхностных явлений дисперсных сред. Молекулярно-кинетическая теория явлений тепломассообмена очень сложна и недостаточно разработана. Поэтому современная теория тепломассообмена в основном феноменологическая, базирующаяся на гидродинамике и термодинамике сплошных сред.

Пособие построено на базе теории переноса любых субстанций. Это позволяет студентам четко понять отличие задач не связанного тепломассообмена от более сложных задач связанного тепломассообмена. Так как математическая формулировка не связанных друг с другом процессов переноса теплоты и массы идентична, то это позволяет ограничиться более подробным изложением задач переноса теплоты.

Пособие «Тепломассообмен» предназначено для заочников дистанционной формы обучения, но может быть рекомендовано и для студентов очной формы обучения по теплоэнергетическим специальностям.

Основные положения учения о процессах переноса тепловой энергии и массы в пространстве

Основные понятия и определения

Перенос любой субстанции (энергии, массы, количества движения, электрического заряда) может происходить как микроскопическим (не види-мым хаотическим тепловым движением микрочастиц), так и макроскопическим (видимым, связанным с движением массы вещества) способами. В первом случае, когда среда неподвижна, перенос массы какого-либо компонента смеси называют диффузией, а перенос тепловой энергии – теплопроводностью. Во втором случае при видимом движении самой среды, которое происходит за счет внешних сил, перенос массы и тепловой энергии называют соответственно конвекцией массы и конвекцией тепла. Различают два вида конвекции: свободную (естественную) и вынужденную. В конвекции первого вида движущая сила обусловлена неоднородностью плотности среды, связанная с неоднородностью температуры, в поле массовой силы (гравитационной, центробежной, электромагнитной). Подогретые объемы среды, имея малую плотность, «всплывают» в охлажденных объемах. При вынужденной конвекции перемещение среды в пространстве осуществляют насосами, вентиляторами и т.д. Совместный перенос массы или тепловой энергии микроскопическим и макроскопическими способами называют соответственно конвективным массо-переносом и конвективным теплопереносом. Движущую среду независимо от агрегатного состояния принято называть жидкостью, которая может быть одно- и многокомпонентной. Конвективный перенос тепла на границе движущейся жидкости и твердой неподвижной стенки называют теплоотдачей. Конвек-тивный перенос массы какого-либо компонента текущей жидкости на границе с твердой неподвижной стенкой называют массоотдачей. Перенос тепла от одной движущейся жидкости к другой движущейся жидкости через разделяющую их твердую неподвижную стенку называют теплопередачей. Таким образом, теплопередача включает в себя теплоотдачу на обеих поверхностях стенки и теплопроводность в самой стенке. Аналогично перенос массы какого-либо компонента движущейся смеси к другой движущейся смеси через разделяющую их твердую неподвижную стенку называют массопередачей. Массопередача включает в себя массоотдачу на обеих поверхностях стенки и диффузию какого-либо компонента в самой стенке.

Перенос тепла может происходить в области глубокого вакуума при исчезающе малом молекулярном содержании вещества. Перенос тепла в этом случае производится фотонами, испускаемыми одними телами и поглощаемыми другими, и называется лучистым теплообменом. При этом по закону эквивалентности массы и энергии переносится и масса. Однако в обычных технических случаях этот перенос массы ничтожно мал по сравнению с лучистым переносом массы, например, при солнечном и звездном излучении.

В общем случае тепло- и массообмен может происходить одновременно. В других случаях их можно рассматривать раздельно либо пренебречь одним из них. Теплообмен может происходить одновременно: и теплопроводностью, и путем переноса тепла движущимся веществом, и излучением. Аналогично массообмен может происходить одновременно: и диффузией какого-либо компонента смеси, и путем переноса этого компонента движущимся веществом. Весьма часто удается выделить и изучить какой-либо частный случай переноса тепла или массы.

Если известны, например, скорость w и температура T в любой точке потока жидкости, а плотность r и удельная массовая теплоемкость с_р ее постоянны, то элементарное количество массы, протекающее в единицу времени через элемент dF произвольной поверхности, равно

,

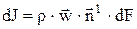где 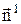– единичный вектор, нормальный к элементарной поверхности dF.

Интегрируя это выражение по всей поверхности, получим поток массы, переносимый конвекцией

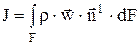, (кг/с). (1.1)

Плотность потока массы равна

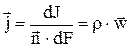, (кг/м²с). (1.2)

Элементарное количество тепла, переносимое в единицу времени через элемент произвольной поверхности dF, составляет

.

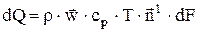Интегрируя по всей поверхности, получим поток тепла, переносимый конвекцией

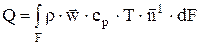, (вт). (1.3)

Плотность потока тепла в этом случае равна

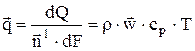, (вт/м²). (1.4)

Поле потенциала. Градиент потенциала

Под потенциалом понимают любую величину, неоднородность которой в пространстве приводит к микроскопическому переносу соответствующей субстанции. Весьма часто его выбирают, исходя из соображений удобства. Например, в случае теплопроводности неоднородными в пространстве будут температура, удельная внутренняя энергия и удельная энтальпия. Однако в качестве потенциала выбирают температуру, поскольку она как функция координат не претерпевает разрыва непрерывности на границе, например, разнородных материалов. Тогда как удельные внутренняя энергия и энтальпия на этой границе как функции координат имеют разрыв непрерывности.

Под полем потенциала понимают совокупность значений потенциала во всех точках изучаемой области для любого момента времени. Если в качестве потенциала выбирают температуру, концентрацию компонента смеси, скорость течения жидкости и т.д., то соответственно речь идет о поле температур, поле концентраций, поле скоростей и т.д. Геометрическое место точек одинаковых потенциалов в потенциальном поле образует изопотенциальные поверхности. Например, в температурном поле ими являются изотермические поверхности. Изопотенциальные поверхности не могут пересекаться. В противном случае в точках пересечения имело бы место несколько потенциалов, что физически абсурдно. Различают нестационарные и стационарные поля потенциалов. Если поле зависит от времени, оно нестационарное. Например, нестационарные поля температур и скоростей течения жидкости в декартовой системе координат имеют вид

T = T(x,y,z,t),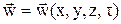

как видно, одно из полей скалярное, а другое векторное.

Соответственно стационарные поля можно записать в виде

;

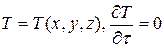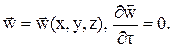
Различают трехмерные, двухмерные и одномерные соответственно нестационарные или стационарные поля потенциалов. Выше представлены соответственно нестационарные и стационарные трехмерные поля температур и скоростей, так как под знаком функции присутствуют три координаты. Например, нестационарные одномерные поля температур и скоростей течения жидкости в декартовой системе координат имеют вид

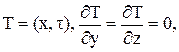
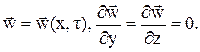
Соответственно стационарные одномерные поля можно записать в виде

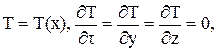
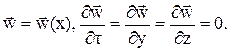
Как видно, стационарность или одномерность поля определяются не только отсутствием времени или соответствующих координат под знаком функции, но и, что важно, равенством нулю частной производной от полей по времени и по соответствующим координатам.

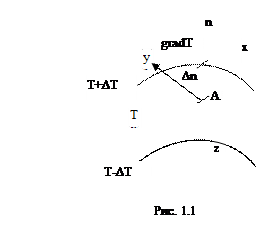
Рассмотрим частный случай двумерного поля потенциала: двумерное температурное поле. На рис. 1.1 представлены три изотермические линии: T-DT, T и T+DT.

Выберем на изотермической линии Т точку А и проведем из нее нормаль к этой линии 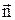. Обозначим расстояние между изотермами Т и Т +D Т через Dn. Градиентом температуры называется предел отношения

, (1.5)

где 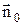– единичный вектор нормали.

Спроектируем градиент температуры на координатные оси

,

,

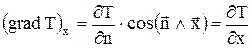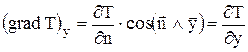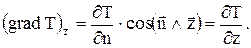
Тогда градиент температуры можно записать в виде

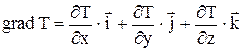. (1.6)

Соответственно модуль градиента температуры равен

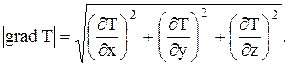(1.7)

Температура – скалярная величина, а градиент температуры – векторная величина. Градиент скорости (векторной величины) является тензором второго ранга, у которого, в отличие от вектора, девять компонентов в проекциях на координатные оси.