Теория принятия статистических решений.
Это чрезвычайно развитая область в экономике, в военном деле, в области обработки информации на фоне шумов и т. д. Рассмотрим элементы этой теории как продолжение теории игр.
Существуют задачи, в которых 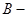 «бессознательный игрок», который мешает принимать нам принимать правильные решения, но он не противодействует активно, а действует в соответствии с природными случайными явлениями, поэтому такую ситуацию называют игрой с природой. Например, помехи в канале связи для передачи информации, шумы при записи или воспроизведении звука и т. д. С другой стороны эта «бессознательность» приводит к непредсказуемому поведению противника. Так в теории игр мы постулируем факт, сознательного поведения противника. Вот почему в теории статистических решений, главным является обоснование критериев оценки различных ситуаций со стороны
«бессознательный игрок», который мешает принимать нам принимать правильные решения, но он не противодействует активно, а действует в соответствии с природными случайными явлениями, поэтому такую ситуацию называют игрой с природой. Например, помехи в канале связи для передачи информации, шумы при записи или воспроизведении звука и т. д. С другой стороны эта «бессознательность» приводит к непредсказуемому поведению противника. Так в теории игр мы постулируем факт, сознательного поведения противника. Вот почему в теории статистических решений, главным является обоснование критериев оценки различных ситуаций со стороны 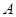 .
.
Мы будем рассматривать дискретные альтернативы (стратегии) природы. Тогда, если у нас 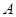 имеется
имеется 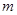 стратегий, а у природы имеется
стратегий, а у природы имеется  альтернатив, то может быть получена матрица выигрышей, при применении каждой пары
альтернатив, то может быть получена матрица выигрышей, при применении каждой пары  .
.  Условия
Условия  иногда называются гипотезами, т. е. возникают как продукты действия со стороны
иногда называются гипотезами, т. е. возникают как продукты действия со стороны 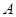 . Если матрица построена, то задача состоит в анализе матрицы с целью получить стратегию
. Если матрица построена, то задача состоит в анализе матрицы с целью получить стратегию  , которая более выгодна по отношению к другим. В простейшем случае, если какие-то строки матрицы заведомо невыгодны, то их можно отбросить и оставить только одну, безусловно лучшую, но обычно это не так. Столбцы платёжной матрицы нельзя отбрасывать, т. к. природа может поступать и в нашу пользу. При анализе платёжной матрицы можно сделать неверный вывод о качестве нашего решения.
, которая более выгодна по отношению к другим. В простейшем случае, если какие-то строки матрицы заведомо невыгодны, то их можно отбросить и оставить только одну, безусловно лучшую, но обычно это не так. Столбцы платёжной матрицы нельзя отбрасывать, т. к. природа может поступать и в нашу пользу. При анализе платёжной матрицы можно сделать неверный вывод о качестве нашего решения.
Пусть сравниваются два выигрыша, находящихся в разных столбцах 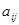 и
и  , причём
, причём  . Если
. Если  , то вроде бы решение в
, то вроде бы решение в  ой строке лучше, чем решение в
ой строке лучше, чем решение в  ой строке, но так просто можно сравнивать, если выигрыш соответствует одинаковым условиям.
ой строке, но так просто можно сравнивать, если выигрыш соответствует одинаковым условиям.
Пример: в Томской области в этом году урожайность пшеницы 20 центнеров с гектара, а в Краснодарской – 25. но эти значения сравнивать нельзя, т. к. для Томской области это оптимальный результат, а для Краснодарской – плохой. Решение нужно сравнивать с потенциальными возможностями.
Вот почему необходимо преобразовывать платёжную матрицу таким образом, чтобы каждый наш выигрыш соотносился с тем максимумом, который можно достигнуть в данных условиях  . Для каждого
. Для каждого  можно найти максимальную величину
можно найти максимальную величину 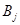 и вычислить величину
и вычислить величину  называемую риском. Здесь
называемую риском. Здесь  . Чем риск меньше, тем лучше.
. Чем риск меньше, тем лучше.
Методы принятия решений в условиях риска.
