Предел и непрерывность композиции функций
Теорема 6. Пусть функция f задана на множестве X, функция f - на множестве Y и f(X) 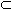 Y. Если существуют конечные или бесконечные пределы
Y. Если существуют конечные или бесконечные пределы
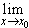 f(x) = y0, f(x) = y0, | (6.40) |
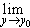 g(y) = z0, g(y) = z0, | (6.41) |
то при x 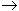 x0 существует предел ( конечный или бесконечный) сложной функции g[ f(x)], причем
x0 существует предел ( конечный или бесконечный) сложной функции g[ f(x)], причем
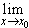 g[ f(x)] = g[ f(x)] = 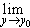 g(y). g(y). | (6.42) |
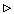 Пусть xn
Пусть xn 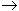 x0, xn
x0, xn 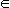 X, n = 1, 2, ...; тогда в силу (6.40) имеем
X, n = 1, 2, ...; тогда в силу (6.40) имеем
yn  f(xn)
f(xn) 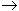 y0, yn
y0, yn 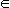 Y, n = 1, 2, ...
Y, n = 1, 2, ...
Поэтому в силу (6.41) g(yn) 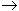 z0, но yn = f(xn), следовательно, g[ f(x)]
z0, но yn = f(xn), следовательно, g[ f(x)] 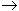 z0, n = 1, 2, ..., т. е. имеет место равенство (6.42).
z0, n = 1, 2, ..., т. е. имеет место равенство (6.42). 
Замечание1. Если функция Y непрерывна в точке y0, т. е.
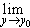 g(y) = g( y0), g(y) = g( y0), | (6.43) |
то формулу (6.42) можно записать в виде
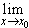 g[ f(x)] = g( g[ f(x)] = g( 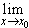 f(x)). f(x)). | (6.44) |
Иначе говоря, предельный переход перестановочен с операцией взятия непрерывной функции. В самом деле, согласно теореме 6
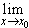 g[ f(x)] g[ f(x)] | = | 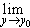 g(y) g(y) | = | g( y0) | = | g( 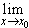 f(x)). f(x)). |
| (6.42) | (6.43) | (6.40) |
Отсюда следует, в частности, что непрерывная функция от непрерывной функции непрерывна, точнее:
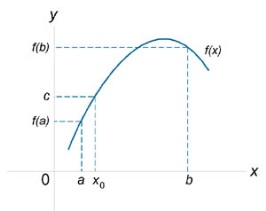
Следствие. Если функция f непрерывна в точке x0, а функция g непрерывна в точке y0 = f(x0), то и их композиция g 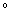 f непрерывна в точке x0.
f непрерывна в точке x0.
 Действительно, непрерывность функции f в точке x0 означает, что
Действительно, непрерывность функции f в точке x0 означает, что
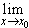 f(x) = f(x0) = y0, f(x) = f(x0) = y0, | (6.45) |
поэтому в силу непрерывности функции g в точке y0 из формулы (6.44) получим
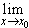 g[ f(x)] g[ f(x)] | = | g[ 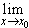 f(x)] f(x)] | = | g f(x0) |
| (6.44) | (6.45) |
т.е. функция g 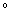 f непрерывна в точке x0.
f непрерывна в точке x0. 
Замечание 2. Обычно, когда говорят, что некоторая функция в данной точке имеет предел, то имеют в виду, что этот предел конечный, а случай бесконечного предела оговаривают особо.
| Непрерывность функций | ||||||
Определение непрерывности по Гейне Говорят, что функция действительного переменного f(x) является непрерывной в точке a∈R (R−множество действительных чисел), если для любой последовательности {xn}, такой, чтоlimn→∞xn=a,выполняется соотношениеlimn→∞f(xn)=f(a).На практике удобно использовать следующие 3 условия непрерывности функции f(x) в точке x=a (которые должны выполняться одновременно):
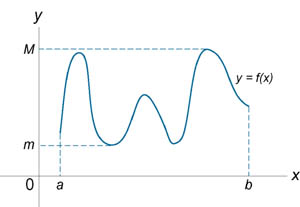
Теорема 7 (Теорема о промежуточном значении). Наши рекомендации
|