Вычисление пределов непрерывных, рациональных и некоторых иррациональных функций.
Определение 1.Число 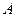
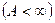 называется пределом функции
называется пределом функции 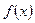 при
при 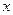 , стремящемся к
, стремящемся к 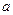
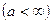 , если для любого числа
, если для любого числа 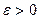 существует число
существует число 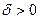 (зависящее от
(зависящее от 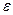 ), такое, что для любого
), такое, что для любого 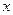 , удовлетворяющего условию
, удовлетворяющего условию 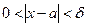 , выполнено неравенство
, выполнено неравенство
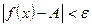 .
.
Пишем: 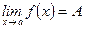 . Говорим: Предел
. Говорим: Предел 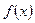 при
при 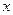 , стремящемся к "
, стремящемся к " 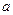 ", равен "
", равен " 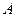 " (или:
" (или: 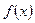 стремится к "
стремится к " 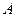 " при
" при 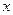 , стремящемся к "
, стремящемся к " 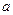 ").
").
Определение 2. Число 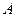 называется пределом функции
называется пределом функции 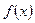 при
при 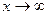
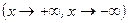 , если для любого числа
, если для любого числа 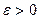 существует число
существует число 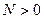 (зависящее от
(зависящее от 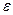 ), такое, что для всех
), такое, что для всех 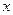 , удовлетворяющих условию
, удовлетворяющих условию
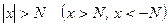 ,
,
выполнено неравенство
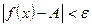 .
.
Пишем: 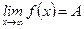 (или
(или 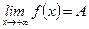 ,
, 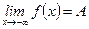 ).
).
Некоторые свойства пределов.
1) 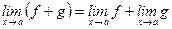 ;
;
2) 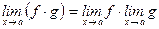 ;
;
3) 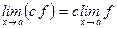 (
( 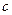 – константа);
– константа);
4) 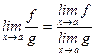 ,
, 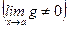 ;
;
5) 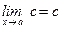 ;
;
6) 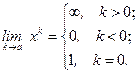
Определение. Функция 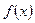 называется непрерывной в точке
называется непрерывной в точке 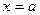 , если: 1)
, если: 1) 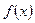 определена при
определена при 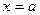 ; 2) существует
; 2) существует 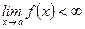 ; 3)
; 3) 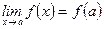 .
.
Теорема. Все элементарные функции непрерывны во всех точках своих областей определения.
Далее мы рассмотрим ряд стандартных пределов (непрерывной, рациональной, иррациональных функций) и сформулируем правила их вычисления.
Вычисление пределов вида 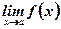 , где
, где 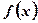 –
–
функция, непрерывная в точке а.
Правило: Воспользоваться формулой:
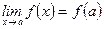 .
.
Примеры:
1) 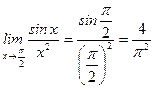 ;
;
2) 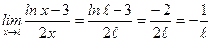 ;
;
Вычисление пределов вида 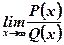 , где
, где 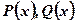 –
–
многочлены (неопределенность вида 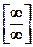 ).
).
Правило:
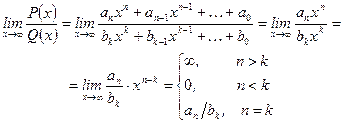
Замечание.Функция 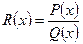 , где
, где 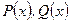 –многочлены, называется рациональной.
–многочлены, называется рациональной.
Примеры:
3) 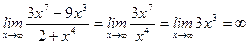 ;
;
4) 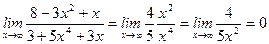 ;
;
5) 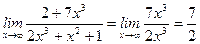 .
.
Вычисление пределов вида 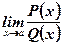 , где
, где 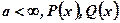 – многочлены, причем
– многочлены, причем 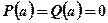
(неопределенность вида 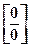 ).
).
Правило.В этом случае надо сократить числитель и знаменатель на 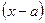 один или несколько раз.
один или несколько раз.
Пример:
6) 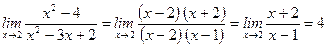 .
.
Замечания.
а)Если 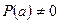 или
или 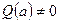 , то предел находим непосредственно.
, то предел находим непосредственно.
Примеры:
7) 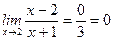 ;
;
8) 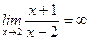 ;
;
9) 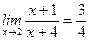 .
.
б)Задачи такого типа составляются и решаются следующим образом. Берем любые числа 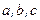 :
:
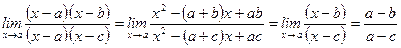 .
.
Вычисление пределов некоторых иррациональных
Функций.
Правило 1. Ввести новую переменную " 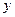 " так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
" так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
Пример.
10) 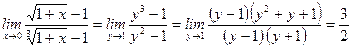 .
.
Мы сделали замену: 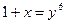 ; при
; при 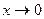
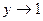 .
.
Правило 2. Перевести иррациональность из числителя в знаменатель или наоборот.
Пример.
11) 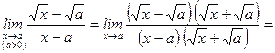
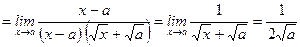 .
.
Умножили числитель и знаменатель на выражение 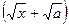 , сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
, сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
Замечание. Задачи такого типа составляются и решаются следующим образом. Берем любые числа 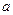 и
и 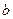 :
:
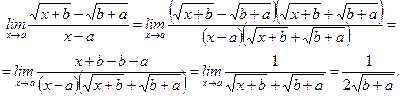
В случае примера 11: 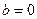 .
.
Правило 3. Разделить числитель и знаменатель на " 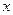 " в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Обычно в этих случаях
" в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Обычно в этих случаях 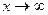 .
.
Пример.
12) 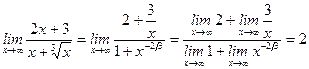 .
.
Задачи для самостоятельного решения
1) 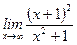 ; 2) ; 2) 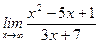 ; 3) ; 3) 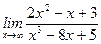 ; 4) ; 4) 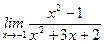 ; 5) ; 5) 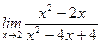 ; 6) ; 6) 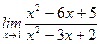 ; 7) ; 7) 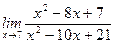 ; 8) ; 8) 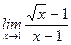 ; ; | 9) 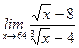 ; 10) ; 10) 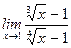 ; 11) ; 11) 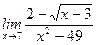 ; 12) ; 12) 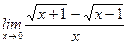 ; 13) ; 13) 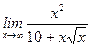 ; 14) ; 14) 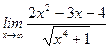 ; 15) ; 15) 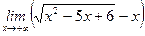 . . |
Ответы:
1)1; 2) 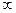 ; 3) 0; 4) -2; 5)
; 3) 0; 4) -2; 5) 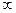 ; 6) 4; 7)
; 6) 4; 7) 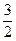 ; 8)
; 8) 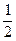 ; 9) 3;
; 9) 3;
10) 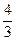 ; 11)
; 11) 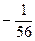 ; 12) 1; 13)
; 12) 1; 13) 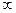 ; 14) 2; 15)
; 14) 2; 15) 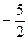 .
.
Занятие 4.
Первый и второй замечательные пределы.
Вычисление пределов вида 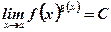 .
.
