Симметриялық құраушылар әдісі
7.1 Симметриялы емес үш фазалы жүйе шамаларының симметриялық құраушылары.
Симметриялы құраушылар әдісі кез келген симметриялы емес үш фазалы жүйе шамаларын (токтар, кернеулер) үш симметриялы жүйе шамаларының қосындысы түрінде көрсутіге негізделген. Жиынтықта симметриялы емес үш фазалы жүйені құратын бұл симметриялық жүйелер симметриялық құраушылар деп аталады. Симметриялық құраушылар бір-бірінен фазалардың алмасу реттіліктермен ерекшеленеді, яғни қалай фазалық шамалар максимум арқылы өту ретімен. Олар тура, кері және нөлдік реттілік жүйлер деп аталады.
Тура, кері және нөлдік реттіліктеріне жататын шамаларды сәйкесті 1,2 және 0 таңбалармен белгілейді (1-сурет)
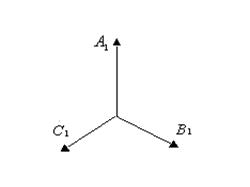
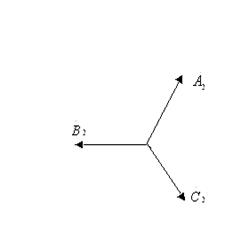
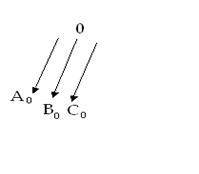
Тура реттілік жүйенің фазалардың алмасу реті А,В, және С. Кері реттілік жүйенің фазалардың алмасу реті А, С, және В. Нөлдік реттілік жүйе бір-бірімен фаза бойынша біртектес үш бірдей шамалардан құралады.
7.1- сурет. Тура (а), кері (в) және нөлдік (с) құраушылар.
Бұл үш жүйелер үшін жазуға болады:
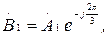
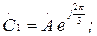 (7.1)
(7.1)
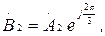
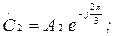 (7.2)
(7.2)
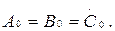 (7.3)
(7.3)
Фазалық көбейтуші 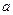 арқылы жазғанда:
арқылы жазғанда:
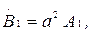
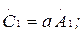 (7.4)
(7.4)
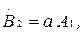
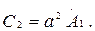 (7.5)
(7.5)
Бұдан басқа 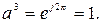 (7.6)
(7.6)
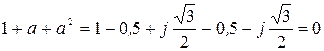 тең және векторлардың симметриялы жүйесін құрады (2-сурет).
тең және векторлардың симметриялы жүйесін құрады (2-сурет).
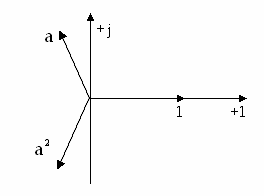 Кез келген
Кез келген 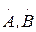 және
және 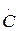 симметриялы емес векторлардың жүйесін тура, кері және нөлдік симметриялық құраушыларға ыдыратуға болатынын дәлелдейік.
симметриялы емес векторлардың жүйесін тура, кері және нөлдік симметриялық құраушыларға ыдыратуға болатынын дәлелдейік.
Егер олай болса, онда
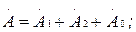
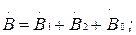
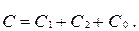
Бұл теңдеулерде симметриялы құраушылардың барлық векторларын (7.3), (7.4) және (7.5) қатынастарын пайданалып 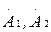 және
және 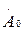 векторлар арқылы көрсетуге болады:
векторлар арқылы көрсетуге болады:
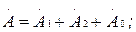 (7.10)
(7.10)
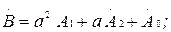 (7.11)
(7.11)
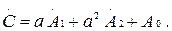 (7.12)
(7.12)
Табылған үш теңдеуден 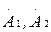 және
және 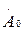 векторларды бір қатарлы белгілеуге болады, ал бұл жағдай берілген симметриялы емес
векторларды бір қатарлы белгілеуге болады, ал бұл жағдай берілген симметриялы емес 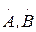 және
және 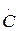 векторлардың жүйесін үш симметриялы жүйелерге ыдырауының мүмкіндігін дәлелдейді.
векторлардың жүйесін үш симметриялы жүйелерге ыдырауының мүмкіндігін дәлелдейді.
(7.10)-(7.12) теңдеулерді қосқаннан кейін шығады:
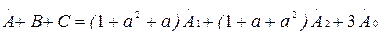 (7.13)
(7.13)
Бұдан (7.6) есепке алғанда 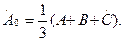 (7.14)
(7.14)
(7.11) теңдеуді а-ға және (7.12) теңдеуді 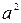 -ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз: 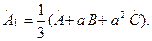
(7.11) теңдеуді 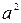 және (7.12) теңдеуді а-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
және (7.12) теңдеуді а-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
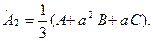 (7.15)
(7.15)
7.2 Токтардың және кернеулердің симметриялы құраушыларына қатысты үш фазалы тізбектердің кейбір қасиеттері
Кернеулердің және токтардың симметриялы емес жүйлері тек апат ережелерде туады. Апат ережелерге бір немесе екі фазалардың қысқа тұйықталуы, фазаның үзіліп ажырауы, электр машиналарда және трансформаторларда пайда болатын симметриялы емес кернеулер мен токтар. Бұл ережерлерді есептеу үшін симметриялы құраушылар әдісі қолданады.
Үш фазалы тізбектерде сызықтық кернеулердің қосындысы нөлге тең, сондықтан сызықтық кернеулерде нөлдік құраушы реттілік болмайды.
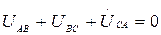
Егер де симметриялы емес ережеде ток бір немесе екі фазада жоқ болса (бір немесе екі фазада үзіліс болса), онда бұл фазалардағы токтардың симметриялық құраушылардың қосындысы нөлге тең.
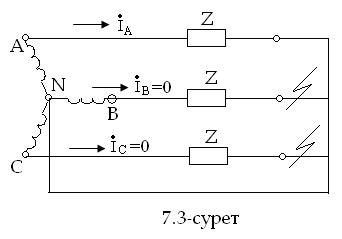
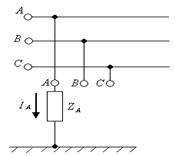
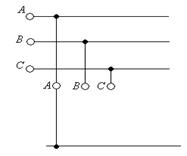
7.3-суретте көрсетелген сүлбеде В және С фазалар ажырап тұр 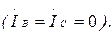 (7.13-7.15) қолданып, табамыз
(7.13-7.15) қолданып, табамыз
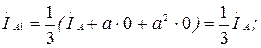
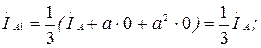
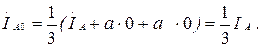
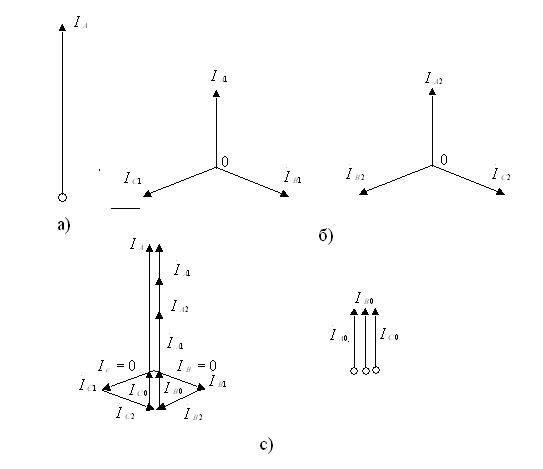
7.4-сурет
7.4-суретте токтың 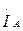 векторы бейнеленген (а) және барлық үш фазалардың токтарының симметриялық құраушылар жүйелердің векторлық диаграммалары келтірілген (в). Токтардың симметриялық құрастырушылардың векторларының қосылуы (с) көрсетіп тұр.
векторы бейнеленген (а) және барлық үш фазалардың токтарының симметриялық құраушылар жүйелердің векторлық диаграммалары келтірілген (в). Токтардың симметриялық құрастырушылардың векторларының қосылуы (с) көрсетіп тұр.
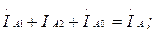
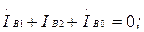
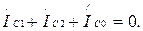
7.3 Токтардың әртүрлі реттіліктері үшін симметриялы үш фазалы тізбектің кедергілері
Егер де симметриялы үш фазалы тізбектің шықпаларына кернеудің тура, кері және нөлдік реттіліктері бар токтардың симметриялы жүйесі ынта салынса, онда бұл тізбекте сол сияқты реттіліктері бар токтардың симметриялы жүйесі пайда болады. Комплексті фазалық кернеудің тура, кері және нөлдік реттіктерінің сәйкесті фазалық комплексті токтардың тура, кері және нөлдік
реттіліктеріне қатынасы сәйкесті тізбектің комплексті кедергісінің тура 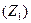 , кері
, кері 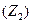 және нөлдік
және нөлдік 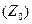 реттіліктері деп аталады.
реттіліктері деп аталады.
Кез келген симметриялы үш фазалы статикалық тізбектерде (айнымалы электр машиналар жоқ тізбектерде) ынта салынған симметриялы кернеулердің ретін тура реттіліктен кері реттілікке ауыстырса токтардың мәндері өзгермейді (оларды тек реттілігі турадан керіге өзгереді). Сондықтан мұндай тізбектер үшін тура және кері реттіліктің келергілері бірдей 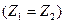 .
.
Тізбекте 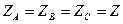 үш фазалы симметриялы тізбекті қарайық (7.5-сурет). Бұл тізбек үшін
үш фазалы симметриялы тізбекті қарайық (7.5-сурет). Бұл тізбек үшін 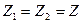 .
.
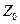 кедергінің мәнін белгілейік.
кедергінің мәнін белгілейік.
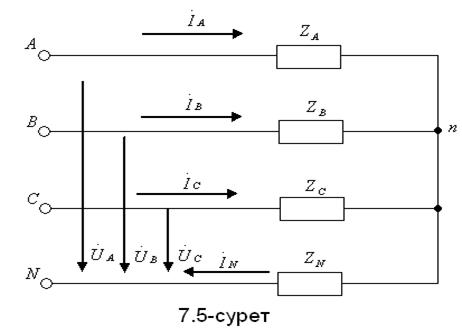
Тізбектің шықпаларына симметриялы жүйесінің фаза кернеулерінің нөлдік реттілігі 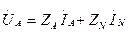 , ал содан кейін
, ал содан кейін 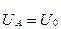 ,
, 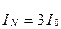 және
және 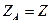 теңдеуге қойып табамыз
теңдеуге қойып табамыз 
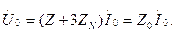 Мұндағы
Мұндағы 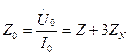 .
.
Бейтарап (нөлдік) сым жоқ кезде нөлдік реттілігі бар ток ақпайды: 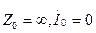 .
.
Тізбектерді симметриялы құраушылар әдісімен есептеген кезде әртүрлі реттіліктегі токтар және кернеулер үшін бөлек сүлбелер қаралады. Бейтарап сымдағы кедергі тура және кері реттіліктердегі симметриялық құраушыларға әсер етпейді, сондықтан бұл үшін токтардың реттіліктеріне құралған сүлбелерде бейтарап сымдағы кедергі көрсетілмейді.
Симметриялық токтардың және кернеулердің нөлдік реттіліктері үшін сүлбеде бейтарап сымдағы 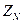 кедергінің орына осы кедергінің еселенген мәнін, яғни 3
кедергінің орына осы кедергінің еселенген мәнін, яғни 3 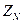 кедергіні әр фазаға енгізеді ( 7.6-сурет). Барлық есептер негізгі деп
кедергіні әр фазаға енгізеді ( 7.6-сурет). Барлық есептер негізгі деп
аталатын бір фаза үшін өткізеді. Әдетте негізгі фаза ретінде А фаза алынады. 7.6 –суретте токтардың және кернеулердің әртүрлі реттіліктері үшін үш бір фазалы сүлбелер көрсетілген. Бұл сүлбелер қысқаша тура, кері және нөлдік реттіліктің сүлбелері деп аталады.
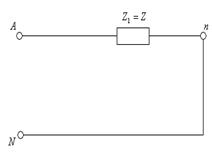
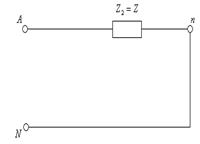
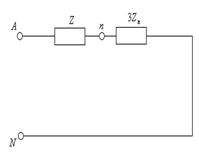
7.6 –сурет
Электр машиналарда 
Симметриялы құраушылар әдісімен есептеген кезде электр қозғалтқыштар үш бөлек тура, кері және нөлдік реттілік сүлбелермен көрсетіледі. Электр генераторлардың сол сияқты сүлбеде 
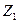 кедергімен тізбектеп фазалық ЭҚК-дің көзі қосылды.
кедергімен тізбектеп фазалық ЭҚК-дің көзі қосылды.
7.4 Симметриялы емес кернеулер жүйесі
Симметриялы емес кернеулер жүйесі қосылған симметриялы тізбекбекте (7.7,б-сурет) токтарды белгілеу үшін, алдымен кернеулердің симметриялық құраушыларын (7.13)-(7.15) кейіптемелерден табамыз:
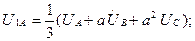
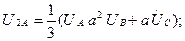
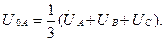
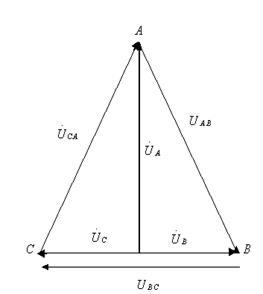
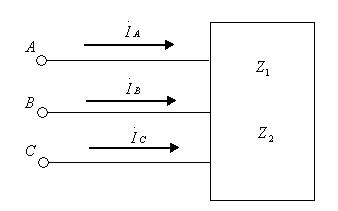
а) б)
7.7-сурет
Токтардың симметриялық құраушылары Ом заңы бойынша анықталады:
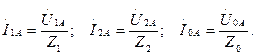
Мысал: Қозғалтқыштың қысқыштарындағы сызықты кернеулер 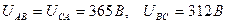 , қозғалтқыштың кедергілері
, қозғалтқыштың кедергілері 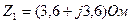 ,
, 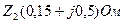 . Сызықты токтарды табу керек
. Сызықты токтарды табу керек
АВС үшбұрыштан табамыз 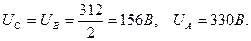
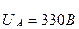 тең деп алсақ, онда
тең деп алсақ, онда 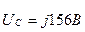 және
және 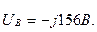
Кернеулердің симметриялық құраушыларын белгілейміз:
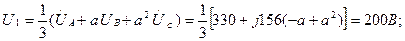
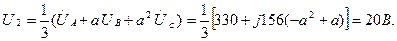
Ом заңы бойынша токтардың симметриялық құраушыларын табамыз:
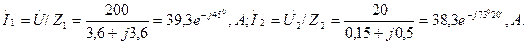
Токтардың симметриялы құраушылары арқылы және (7.10)-(7.12) кейіптемелерді қолданып сызықты токтарды табамыз:
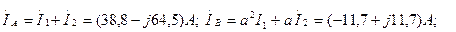
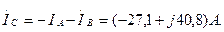
Токтардың әрекет мәндері:
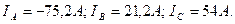
7.5 Симметриялы емес үш фазалы тізбекте токтардың және кернеулердің симметриялық құраушылары:
а) симметриялы емес жүктемесі бар тізбекті есептеу
Әдетте симметриялы емес ережелер апатты жағдайда пайдалы болады.
Симметриялы емес жағдайда екі түрге көлденеңдік және бойлық деп ажыратуға болады. Көлденеңдік симметриясыздық үш фазалы тізбекке симметриялы емес жүктемені қосқан кезде пайда болады. Оларға қатысты әртүрлі қысқа тұйықталудың түрлері (фазалар арасындағы қысқа тұйықталу, бір немесе екі фазаның жерге қосылуы). Бойлық симметриясыздық фазаларға бірдей емес кедергілер қосылғанда немесе желінің бір немесе екі фазаның сымдары үзілсе (симметриялы емес желі бөлігі) пайда болады.
Үш фазалы тізбектердегі симметриялы емес ережелерді есептеу кезде теңгермелік принципті қолданады. Ол үшін симметриялы емес жүктемені немесе симметриясыз бөлігін кернеу көздерімен ауыстырады, олардың мәндерін есептеу біткенше өзгермейді. Осындай ауыстырудан кейін барлық тізбек симметриялы құраушылары бір-біріне тәуелді емес.
Құрамында симметриялы динамикалық  және симметриялы емес статикалық жүктемелері бар сүлбені (7.8-сурет) симметриялы құраушылар әдіспен есептеуді қарап шығайық.
және симметриялы емес статикалық жүктемелері бар сүлбені (7.8-сурет) симметриялы құраушылар әдіспен есептеуді қарап шығайық.
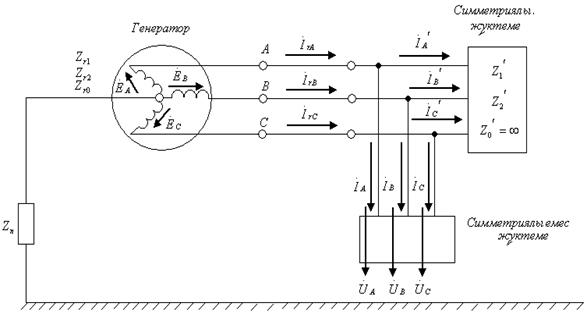
7.8-сурет
Генератордың ЭҚК-і және сүлбенің элементтерінің кедергілері берілген.
Токтарды және кернеулерді табу керек.
Симметриялы емес жүктемені алып 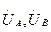 және
және 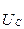 кернеулері бар үш ЭҚК көздерімен ауыстырамыз.
кернеулері бар үш ЭҚК көздерімен ауыстырамыз.
А фазаның негізгі фаза ретінде алып 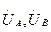 және
және 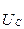 кернеулері
кернеулері 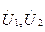 және
және 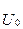 симметриясы құраушылары жіктейміз, сонда симметриялы сүлбені аламыз (7.9-сурет).
симметриясы құраушылары жіктейміз, сонда симметриялы сүлбені аламыз (7.9-сурет).
Демек симметриялы емес жүктемелер орына үш көректендіргіш көздер жүйесі кернеулерінің тура, кері және нөлдік реттіліктері орын алады.
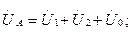
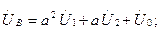
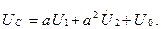
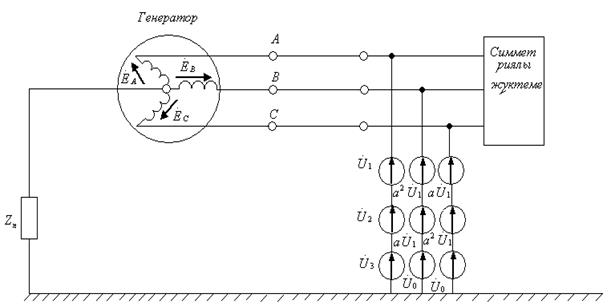
7.9-сурет
Симметриялы тізбекте симметриялы кернеулер жүйесінің кейбір реттілігі симметриялы токтар жүйесінің сол реттілігін туғызады. Сондықтан, үш бір-біріне тәуелсіз сүлбелерді құруға болады (7.10-сурет).
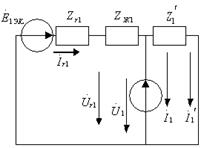
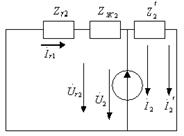
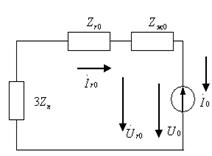
а) б) в)
7.10-сурет
Тура, кері реттілік сүлбе түрлері әр уақытта бірдей, сүлбенің нөлдік реттілігі әдетте ерекше. Бұл мысалды нөлдік реттілік тармақсыз болады, себебі 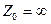 .
.
Бейтарап сымның кедергісі сүлбеде 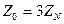 тең екенін есте сақтау керек. Содан кейін есетті өткізу үшін бөлек реттіліктердің сүлбелерін қарапайым түрге келтіреміз, бұл кезде белгісіз
тең екенін есте сақтау керек. Содан кейін есетті өткізу үшін бөлек реттіліктердің сүлбелерін қарапайым түрге келтіреміз, бұл кезде белгісіз 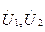 және
және 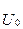 кернеулер бар тармақтарға тиіспей қою керек.
кернеулер бар тармақтарға тиіспей қою керек.
(10,а)–суреттегі сүлбені түрлендіру үшін генератордың және симметриялы қабылдағыштың тармақтарын эквивалентті генератормен ауыстырамыз.
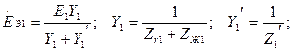
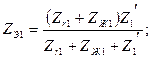
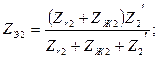
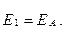
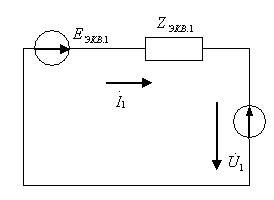
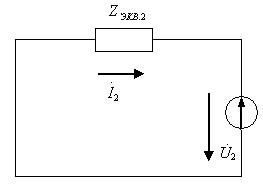
а) б)
7.11-сурет
Тура (а), кері(б) реттіліктердің эквивалентті сүлбелері. Осы мысалда нөлдік реттіліктің сүлбесін, қарапайым болғандықтан, түрлендіру қажетті емес.
Әрбір үш сүлбе үшін Корхгофтың екінші заңы бойынша теңдеулерді жазамыз:
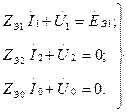
мұндағы 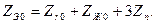
Бұл үш теңдеуде алты белгісіз 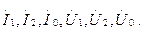
Бұл алты белгісіздерін байланыстыратын қосымша үш теңдеу берілген сүлбе және симметриялы емес қабылдағыштың параметрлері арқылы құрылады.
(7.12,а)-суреттегі қабылдағыш үшін
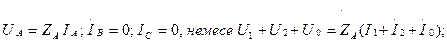
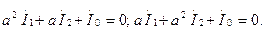
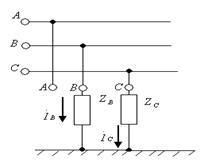
(7.12,б)-суреттегі қабылдағыш үшін
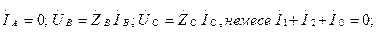
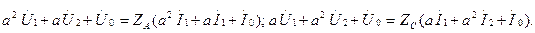
а) б)
7.12-сурет 7.13-сурет
Статикалық симметриялы емес жүктеменің басқа түрлеріне осындай ұқсастық бойынша қосымша теңдеулер құрылады.
Негізгі және қосымша теңдеулерді біріктіріп шешіп А фаза тоғының симметриялы құраушыларын анықтайды (симметриялы емес тармақтарында). Содан кейін тура, кері және нөлдік реттіліктердің сүлберін бөлек тармақтары бойынша осы құраушылардың тарауын табады. Кез-келген тармақта токтардың құрастырушыларын тапқаннан кейін әрбір фазадағы нақтылы токты анықтайды және әртүрлі реттіліктердің кернеу түсудің құраушыларын анықтайды, ал содан кейін сүлбенің бөлек бөліктеріндегі фазалық кернеулерді белгілейді.
7.13-суретте көрсетілген сүлбенің ережесін есептейміз.
Қосымша теңдеулерді құрамыз:
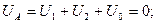
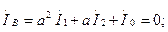
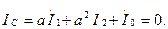
(7.21) теңдеуде (7.20) алып, табамыз 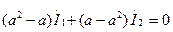 немесе
немесе 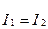 . Бұл нәтижені (7.20) теңдеуге қойып табамыз
. Бұл нәтижені (7.20) теңдеуге қойып табамыз 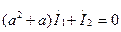 , ал бұдан
, ал бұдан 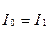 шығады.
шығады.
(7.18) 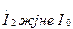 токтарды
токтарды 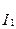 тоққа ауыстырып, ал содан кейін үш теңдеуді қосып (7.19) теңдеуді еске алып, табамыз
тоққа ауыстырып, ал содан кейін үш теңдеуді қосып (7.19) теңдеуді еске алып, табамыз
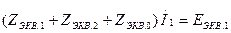
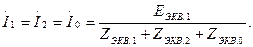
Кернеудің симметриялы құраушылары (жерге тұйықталған жерде) (7.18) теңдеулерден белгіленеді:
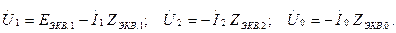
7.10,а суреттегі сүлбе үшін токтар тең: 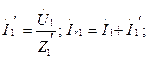
7.10,б суреттегі сүлбе үшін:
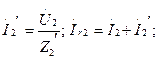
7.10,в суреттегі сүлбе үшін:
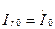 .
.
Генератордың шықпаларындағы кернеулердің симметриялы құраушылар: 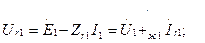
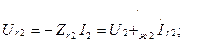
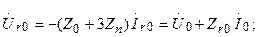
б) желінің симметриялы емес бөлігі бар тізбекті есептеу әдісін қарастырамыз. Генератордың ЭҚК және сүлбедегі элементтердің кедергілері берілген. Токтарды және кернеулерді табу керек.
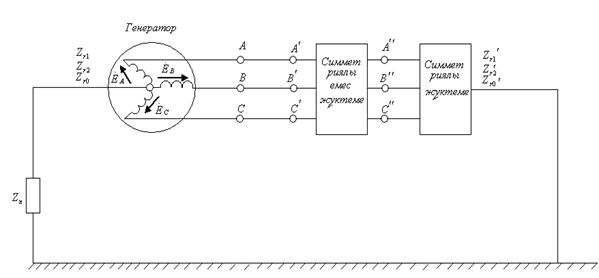
7.14-сурет. Бойлық симметриясыздық сүлбе
Сүлбенің симметриялы емес бөлігіндегі кернеулері 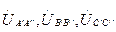 белгісіз. Оларды үш энергия көзімен ауыстырып кернеулерді
белгісіз. Оларды үш энергия көзімен ауыстырып кернеулерді 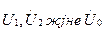 симметрялы құраушыларына ажыратамыз. Содан кейін А фазасын негізгі деп алып тура, кері және нөлдік реттіліктеріне үш сүлбе құрамыз (14- сурет).
симметрялы құраушыларына ажыратамыз. Содан кейін А фазасын негізгі деп алып тура, кері және нөлдік реттіліктеріне үш сүлбе құрамыз (14- сурет).
Бұл сүлбелер үшін Кирхгофтың екінші заңы бойынша теңдеулер жазамыз:
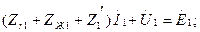
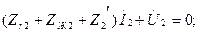
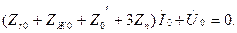
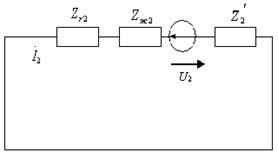
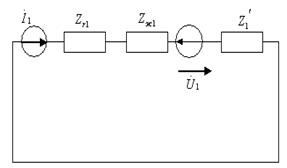
а) б)
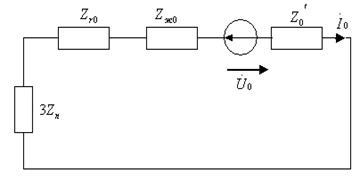
в)
7.15-сурет. Тәуелсіз үш симметриялы құраушылар сүлбелері.
Бұл үш теңдеулерде алты белгісіз бар: 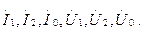
Осы сүлбелерге сүйеніп және тізбектің симметриялы емес бөлігіндегі параметрлеріне сүйеніп қосымша үш теңдеуді құрамыз.
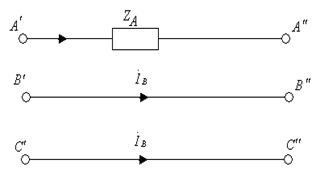
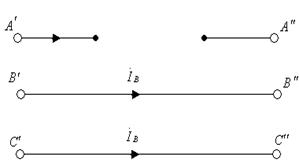
а) б)
7.16-сурет. Әртүрлі симметриялы емес сүлбелер
7.15,а-суретте келтірілген қосымша үш теңдеу
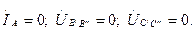
Қосымша теңдеулердегі кернеулерді және токтары олардың симметриялы құраушылары арқылы көрсету керек.
Негізгі және қосымша теңдеулерді біріктіріп шығарып токтардың симметриялы құраушыларын табамыз, содан кейін кернеулердің симметриялы құраушыларын анықтаймыз.
Симметриялы құраушылар арқылы нақтылы токтарды және кереулерді табамыз .
Сегізінші тарау
8 Синусоидалсыз токтар
8.1 Синусоидалсыз ЭҚК-тер, кернеулер және токтар
Айнымалы токтың генераторларында саңылау бойында магнитиндукцияның қисығының тарауы синусоидан айрықша болғандықтан орамадағы пайда болған ЭҚК-тердің қисықтары синусоидалды емес.
Сызықсыз кедергілері, индуктивтіктері және сыйымдылықтары бар тізбектерде (мысалы, түзіткіштер, электр доғалар, болат өзекшесі бар орауыштар) ЭҚК-тер синусоидалды болса да токтар және кернеулер синусоидалды емес болады.
8.1,а-суретте реакторы бар тізбектегі ток, ал 8.1,б-суретте басқарылатын түзеткіш (тиристор) бар тізбектегі ток.
Периодикалы серпіндердің генераторлары радиотехниканың, автоматиканың, есептеу техниканың әртүрлі құрылғыларында және автоматталған басқару жүйелерде қолданады.
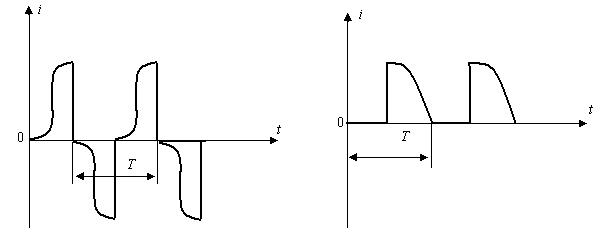
а) б)
8.1-сурет
Серпіндердің түрлері әртүрлі болады: ара тәрізді (8.2.а-сурет), сатылы (8.2.б-сурет), және тура бұрышты (8.2.б-сурет).
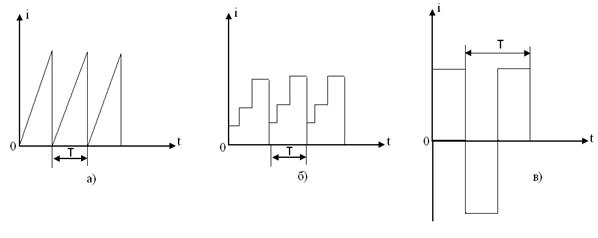 8.2-сурет
8.2-сурет
8.2-суреттегі қисықтардың бәріде периодикалы және олар синусоидалсыз периодикалы токтардың мысалдардың көрсетеді.
8.2 Синусоидалсыз периодикалы қисықты тригонометриялық қатарға жіктеу
Дирихленің жағдайын қанағаттандыратын 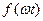 функция Эйлер-Фурьенің тригонометриялық қатарына жіктеледі:
функция Эйлер-Фурьенің тригонометриялық қатарына жіктеледі:
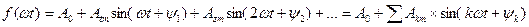 (8.1)
(8.1)
Қатардың бірінші мүшесі 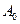 тұрақты құраушысы немесе нөлдік гармоникасы деп аталады, екінші мүше
тұрақты құраушысы немесе нөлдік гармоникасы деп аталады, екінші мүше 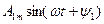 -негізгі синусоида немесе бірінші гермоника, барлық қалған мүшелер түрі
-негізгі синусоида немесе бірінші гермоника, барлық қалған мүшелер түрі 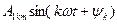 , ал k>1 болғанда –жоғары гармоникалар деп аталады;
, ал k>1 болғанда –жоғары гармоникалар деп аталады; 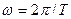 -негізгі бұрыштық жиілік; Т-синусоидалсыз периодикалы функцияның периоды.
-негізгі бұрыштық жиілік; Т-синусоидалсыз периодикалы функцияның периоды.
Әрбір гармониканың қосындының синусын ашқаннан кейін тригонометриялық қатар мына түрде жазылады:
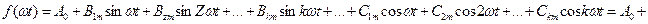
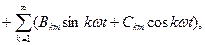 (8.2)
(8.2)
мұндағы 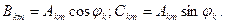
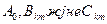 коэффициенттер келесі интегралдар арқылы есептеуге болады:
коэффициенттер келесі интегралдар арқылы есептеуге болады: 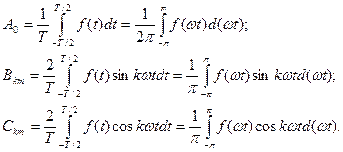 (8.3)
(8.3)
(8.2) қатардың коэффициенттерін білгенде (8.1) түрге жеңіл ауысуға болады
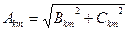 және
және 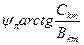 .
.
1. Егерде 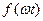 функция ординат білікке симметриялы болса, яғни
функция ординат білікке симметриялы болса, яғни 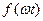 =
= 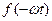 , онда ол жұп функция (8.3-сурет).
, онда ол жұп функция (8.3-сурет).
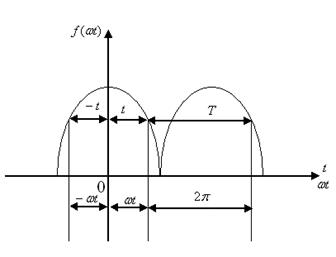
Қандай да болған жиіліктің синусоидалары тақ болғандықтан, олар қатардың құрамасына кірмейді, сондықтан
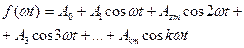 (8.4)
(8.4)
8.3-сурет
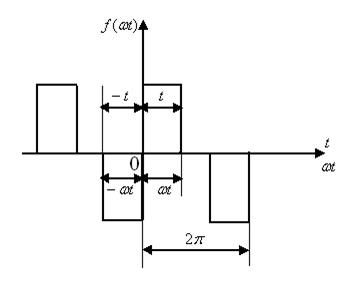 2. Егер де
2. Егер де 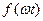 функция координат басына симметриялы болса, яғни
функция координат басына симметриялы болса, яғни 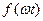 =-
=- 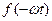 , онда ол тақ функция (8.4-сурет). Мұндай функциялар тұрақты құраушылары және косинустары жоқ қатарға жіктеледі
, онда ол тақ функция (8.4-сурет). Мұндай функциялар тұрақты құраушылары және косинустары жоқ қатарға жіктеледі
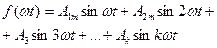 (8.5)
(8.5)
8.4-сурет
3. Егер де 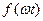 функция абцисс білікке симметриялы болса, яғни
функция абцисс білікке симметриялы болса, яғни 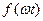 =-
=- 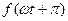 , онда ол тұрақты құраушылары және жұп гармоникалары жоқ қатарға жіктеледі (8.5-сурет).
, онда ол тұрақты құраушылары және жұп гармоникалары жоқ қатарға жіктеледі (8.5-сурет).
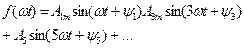 (8.6)
(8.6)
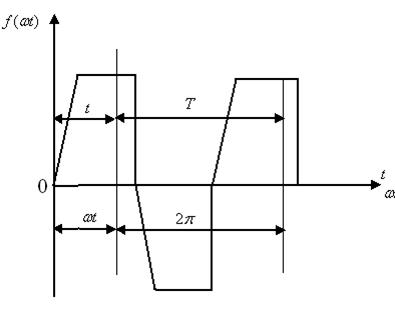
8.5-сурет
8.3 Синусоидалсыз периодикалы ЭҚК-тердің, кернеулердің және токтардың максималды, әрекет және орташа мәндері
Синусоидалсыз периодикалы шамалар келесі үш мәнмен сипатталады:
а)максималды мәні 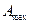 ; (8.7)
; (8.7)
б) модуль (шама) бойынша орташа мәні
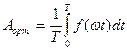 ; (8.8)
; (8.8)
в) әрекет мәні
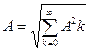 . (8.9)
. (8.9)
Сонымен синусоидалсыз периодикалы шаманың әрекет мәні тек оның гармоникаларының әрекет мәндеріне тәуелді, ал олардың 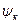 басты фазаларынан тәуелсіз, яғни
басты фазаларынан тәуелсіз, яғни
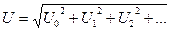 ;
; 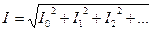 (8.10)
(8.10)
8.4 Синусоидалсыз периодикалы қисықтардың түрін сипаттайтын коэффициенттер
Синусоидалсыз периодикалы қисықтарды бағалаған кезде электр энергетикада 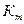 қисық түрінің коэффициентімен,
қисық түрінің коэффициентімен, 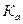 амплитуданың коэффенцитімен және
амплитуданың коэффенцитімен және 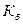 бұрмалау коэффициентімен пайдаланады.
бұрмалау коэффициентімен пайдаланады.
а) түрінің коэффициенті әрекет мәнінің орташа мәніне қатынасы деп белгіленеді:
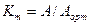 (8.11)
(8.11)
синусоида үшін 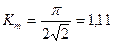 ;
;
б) амплитуданың коэффициенті-максималды мінінің әрекет мәніне қатынасы деп белогілінеді:
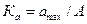
синусоида үшін 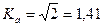 ; (8.12)
; (8.12)
в) бұрмалану коэффициенті –негізгі гармониканың әрекет мәнінің барлық қисықтың әрекет мәніне қатынасы деп белгіленеді:
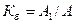 (8.13)
(8.13)
синусоида үшін 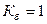 .
.
8.5 Синусоидалсыз периодикалы ЭҚК-тер, кернеулер және токтар бар тізбектерді есептеу
Егер де тізбекте бір немесе бірнеше синусоидалсыз периодикалы ЭҚК-тердің көздері болса, онда есептеу үш кезеңге бөлінеді:
а) көздердің ЭҚК-терін тұрақты және синусоидалды құраушыларға жіктеу;
б) тізбектегі токтарды және кернеулерді әрбір құраушы үшін бөлек есептеу;
в) беттесу принципін қолданып әрбір құраушы үшін табылған шешімді бірлесіп қарау.
Егер де ЭҚК (8.6,а –сурет) тең 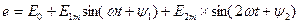 онда мұнда ЭҚК-тердің көзінің әрекеті үш тізбекті қосылған ЭҚК-тердің әрекетіне ұқсас (8.6,б-сурет ).
онда мұнда ЭҚК-тердің көзінің әрекеті үш тізбекті қосылған ЭҚК-тердің әрекетіне ұқсас (8.6,б-сурет ).
Мұндағы 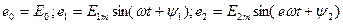 (8.14)
(8.14)

а) б)
8.6-сурет
Әрбір ЭҚК-тің әрекетін бөлек қарап, ал содан кейін беттесу принципті қолданып тізбектің барлық бөліктеріндегі токтардың құраушыларын табамыз.
Тізбектегі токтың лезді мәні құрастырушы токтардың лезді мәндерінің қосындысына тең, яғни 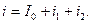
Сонымен синусоидалсыз ЭҚК-тері бар сызықты тізбектерді есептеу синусоидалды ЭҚК-тері бар 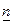 есептерді шешуге келтіреді, мұндағы
есептерді шешуге келтіреді, мұндағы 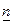 -әртүрлі
-әртүрлі
жиіліктері бар ЭҚК-тердің синусоидалды құрастырушылардың саны және тұрақты ЭҚК-і бар бір есеп.
Шешу кезде, әртүрлі жиілік үшін, индуктивтік және сыйымдылық кедергілері бірдей емес екенін еске алу керек. 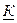 -гармоника үшін индуктивтік кедергі бірінші гармоникаға қарағанда
-гармоника үшін индуктивтік кедергі бірінші гармоникаға қарағанда 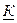 есе үлкен , ал сыйымдылық кедергі-
есе үлкен , ал сыйымдылық кедергі- 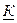 есе кіші:
есе кіші:
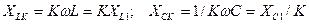 (8.15)
(8.15)
Активтік кедергі тұрақты ток кезіндегіге тең. Әрбір гармониканы есептеген кезде комплекстерді қолдануға болады және әрбір гармоника үшін векторлық диаграммаларды салуға болады.
8.6 Синусоидалсыз ток тізбегіндегі қуаттар
Синусоидалсыз периодикалы токтың активтік қуат-период бойынша орта қуат деп белгіленеді
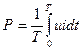 (8.16)
(8.16)
Егер де кернеудің және токтың лезді мәндерін тригонометриялық қатар түрінде білдірсек, онда табамыз
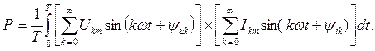
Период ішіндегі әртүрлі жіліктері бар синусоидалардың лезді мәндерінің көбейтулері нөлге тең болғандықтан, шығады
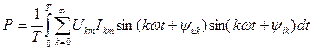 .
.
Интегралдаудан кейін табамыз
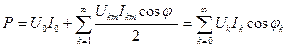 , (8.17)
, (8.17)
мұндағы 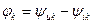
Синусоидалсыз токтың орташа активтік қуаты бөлек гармоникалардың орташа қуаттардың қосындысына тең (тұрақты құраушысы 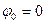 тең нөлдік гармоника ретінде қаралады):
тең нөлдік гармоника ретінде қаралады):
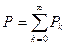 . (8.18)
. (8.18)
Сикусоидалсыз токтың реактивтік қуаты бөлек гармоникалардың реактивтік қуаттарының қосындысына тең:
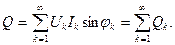 (8.19)
(8.19)
Синусоидалсыз токтың толық қуаты токтың және кернеудің әрекет мәндерінің көбейтіндісі ретінде табылады:
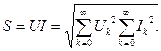 (8.20)
(8.20)
Синусоидалсыз токтар кезде қуат коэффициент активтік қуаттың толық қуат қатынасына тең
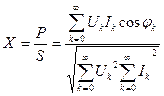 (8.21)
(8.21)
(8.21) қатынас тек u және i арасында тұра пропорционал болғанда бірге тең, яғни тізбектің кедергісі таза активтік кезде 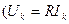 және
және 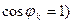 . Бір қисықта (кернеуде немесе токта) екінші қисықта жоқ гармониканың болуы активтік және реактивтік қуаттардың шамаларына әсер етпейді, бірақ бұл гармоникалардың құрамында сақтайтын функцияның әрекет мәнін өсіреді. Сондықтан, егер де қаралып жатқан тізбектегі толық қуатты кернеудің және токтың әрекет мәндерінің көбейтіндісі, яғни S=UI деп белгіленген, онда синусоидалды ережеден айрықша синусоидалсыз тізбекте активтік және реактивтік қуаттардың шаршыларының қосындылары қуаттың шаршысына тең емес:
. Бір қисықта (кернеуде немесе токта) екінші қисықта жоқ гармониканың болуы активтік және реактивтік қуаттардың шамаларына әсер етпейді, бірақ бұл гармоникалардың құрамында сақтайтын функцияның әрекет мәнін өсіреді. Сондықтан, егер де қаралып жатқан тізбектегі толық қуатты кернеудің және токтың әрекет мәндерінің көбейтіндісі, яғни S=UI деп белгіленген, онда синусоидалды ережеден айрықша синусоидалсыз тізбекте активтік және реактивтік қуаттардың шаршыларының қосындылары қуаттың шаршысына тең емес: 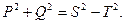
Т шама бұрмалау қуат деп аталады.
Егер де тізбектің кедергісі активтік болса, онда токтың және кернеудің қисықтары түрлес. Бұл жағдайда Q=0 және Т=0.
8.7 Үш фазалы тізбектерде қалыптасқан ереже
Үш фазалы тізбектерде қалыптасқан ереже кезінде екінші және үшінші фазалардағы токтың және кереудің қисықтары бірінші фазадағы үштен бір периодқа ығысқан токтың және кернеудің қисығына түрлес. Егер де А фазадағы кернеу 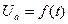 уақыт функциямен көрсетілсе, онда
уақыт функциямен көрсетілсе, онда 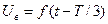 және
және 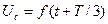 , мұндағы Т-негізгі жиіліктің периоды.
, мұндағы Т-негізгі жиіліктің периоды.
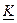 ретті гармониканың
ретті гармониканың 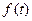 функцияны барлық үш фазада қарайық
функцияны барлық үш фазада қарайық 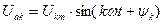 болсын.
болсын.
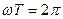 тең екенін еске алып және t орнына сәйкесті
тең екенін еске алып және t орнына сәйкесті 
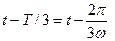 және
және 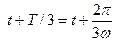 қойып, табамыз:
қойып, табамыз:
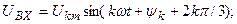
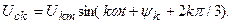
Гармоникалардың реті үшке еселі (k=3n, мұнда n-бүтін сан) кернеулердің барлық фазаларда кез келген уақытта шамалары және бағыттары бірдей.
K=3n+1 кезде үш фазаның гармоникалары симметриялы кернеу жүйені құрады. Жүйенің реттілігі бірінші гармониканың реттелігімен дәл түседі.
K=3n+2 кезде үш фазаның гармоникалары симметриялы кернеу жүйені құрады. Жүйенің реттелігі бірінші гармониканың кері реттілігімен дәл түседі.
Сонымен 1,4,7,10,13 және т.б.реті бар гармоникалар тура реттілігі бар кернеу жүйесін, 2,5,8,11,14 және т.б. реті бар гармоникалар кері реттілігі бар кернеу жүйесін құрса, ал 3,6,9,12 және т.б. реті бар гармоникалар нөлдік реттілігі бар кернеу жүйесін құрады.
Егер де әрбір фазаның кернеуінде тұрақты құраушысы болса, онда ол нөлдік реті бар гармоника деп қаралады, яғни нөлдік реттілікті құрады.
Көпшілік жағдайда кернеулерде тұрақты құраушы және жұп гармоникалар жоқ болады.
Үш фазалық тізбектердің әртүрлі сүлбелерін қарайық.
Егер де генератордың фазалары жұлдызша қосылған болса, онда фазалы синусоидалсыз кернеулер реті үшке еселі кернеулердің гармоникалары құрамында жоқ, себебі олар нөлдік реттіліктегі жүйені құрады.
Фазалық кернеу 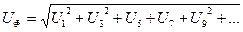
Сызықты кернеу 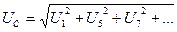
Бұдан шығады 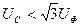 .
.
Симметриялы жүктеме кезде негізгі жиіліктің және жоғары гармоникалар реті үшке еселі жоғары гармоникаларды қоспағанда, тура және кері реттелігі бар жүйелерді құрады да қосындылары нөлді береді. Ал реті үшке еселі гармоникалар нөлдік реттелігі бар жүйені құрады, яғни кез келген уақытта олардың мәндері және бағыттары бірдей болады. Сондықтан, нөлдік сымдағы ток нөлдік реттелігі бар жоғары гармоникалардың қосындысының үш есесіне тең: 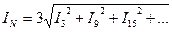
Бейтарап сым жоқ кезде әрбір фазадағы токтың құрамында реті үшке еселі жоғары гармоникалар жоқ. Сондықтан, қабылдағышта нөлдік реттелігі бар токтардан кернеулер жоқ.
Егер де генератордың фазалары үшбұрышқа қосылса, онда фазадағы ЭҚК-тер синусоидалсыз болғанда генератордың тұйықталған контурында әрекет етуші ЭҚК-тердің қосындысы нөлге тең емес, ол реті үшке еселі жоғары гармоникалардың қосындысының үш есесіне тең:
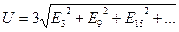
Егер де фазалар тұйықталған үшбұрышқа қосылса, онда реті үшке еселі ЭҚК-тердің гармоникалар генератордың ішкі тоғын туғызады
Генератордың фазалық тоғы
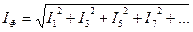
Сыртқы тізбектегі сызықтық ток
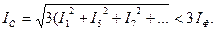
Бұл үш жүйелер үшін жазуға болады:
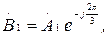
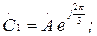 (7.1)
(7.1)
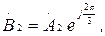
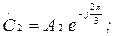 (7.2)
(7.2)
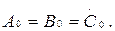 (7.3)
(7.3)
Фазалық көбейтуші 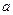 арқылы жазғанда:
арқылы жазғанда:
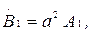
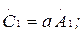 (7.4)
(7.4)
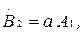
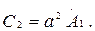 (7.5)
(7.5)
Бұдан басқа 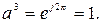 (7.6)
(7.6)
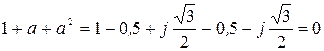 тең және векторлардың симметриялы жүйесін құрады (2-сурет).
тең және векторлардың симметриялы жүйесін құрады (2-сурет).
 Кез келген
Кез келген 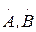 және
және 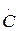 симметриялы емес векторлардың жүйесін тура, кері және нөлдік симметриялық құраушыларға ыдыратуға болатынын дәлелдейік.
симметриялы емес векторлардың жүйесін тура, кері және нөлдік симметриялық құраушыларға ыдыратуға болатынын дәлелдейік.
Егер олай болса, онда
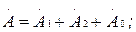
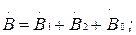
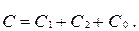
Бұл теңдеулерде симметриялы құраушылардың барлық векторларын (7.3), (7.4) және (7.5) қатынастарын пайданалып 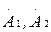 және
және 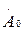 векторлар арқылы көрсетуге болады:
векторлар арқылы көрсетуге болады:
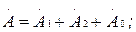 (7.10)
(7.10)
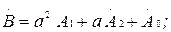 (7.11)
(7.11)
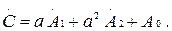 (7.12)
(7.12)
Табылған үш теңдеуден 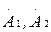 және
және 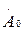 векторларды бір қатарлы белгілеуге болады, ал бұл жағдай берілген симметриялы емес
векторларды бір қатарлы белгілеуге болады, ал бұл жағдай берілген симметриялы емес 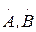 және
және 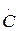 векторлардың жүйесін үш симметриялы жүйелерге ыдырауының мүмкіндігін дәлелдейді.
векторлардың жүйесін үш симметриялы жүйелерге ыдырауының мүмкіндігін дәлелдейді.
(7.10)-(7.12) теңдеулерді қосқаннан кейін шығады:
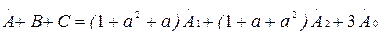 (7.13)
(7.13)
Бұдан (7.6) есепке алғанда 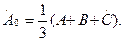 (7.14)
(7.14)
(7.11) теңдеуді а-ға және (7.12) теңдеуді 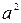 -ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз: 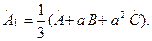
(7.11) теңдеуді 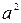 және (7.12) теңдеуді а-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
және (7.12) теңдеуді а-ға көбейтіп, ал содан кейін (7.10)-(7.12) теңдеулерді қосып табамыз:
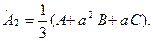 (7.15)
(7.15)
7.2 Токтардың және кернеулердің симметриялы құраушыларына қатысты үш фазалы тізбектердің кейбір қасиеттері
Кернеулердің және токтардың симметриялы емес жүйлері тек апат ережелерде туады. Апат ережелерге бір немесе екі фазалардың қысқа тұйықталуы, фазаның үзіліп ажырауы, электр машиналарда және трансформаторларда пайда болатын симметриялы емес кернеулер мен токтар. Бұл ережерлерді есептеу үшін симметриялы құраушылар әдісі қолданады.
Үш фазалы тізбектерде сызықтық кернеулердің қосындысы нөлге тең, сондықтан сызықтық кернеулерде нөлдік құраушы реттілік болмайды.
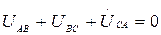
Егер де симметриялы емес ережеде ток бір немесе екі фазада жоқ болса (бір немесе екі фазада үзіліс болса), онда бұл фазалардағы токтардың симметриялық құраушылардың қосындысы нөлге тең.

7.3-суретте көрсетелген сүлбеде В және С фазалар ажырап тұр 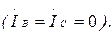 (7.13-7.15) қолданып, табамыз
(7.13-7.15) қолданып, табамыз
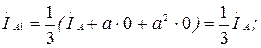
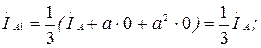
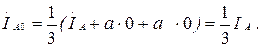

7.4-сурет
7.4-суретте токтың 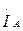 векторы бейнеленген (а) және барлық үш фазалардың токтарының симметриялық құраушылар жүйелердің векторлық диаграммалары келтірілген (в). Токтардың симметриялық құрастырушылардың векторларының қосылуы (с) көрсетіп тұр.
векторы бейнеленген (а) және барлық үш фазалардың токтарының симметриялық құраушылар жүйелердің векторлық диаграммалары келтірілген (в). Токтардың симметриялық құрастырушылардың векторларының қосылуы (с) көрсетіп тұр.
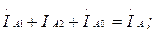
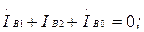
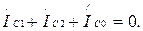
7.3 Токтардың әртүрлі реттіліктері үшін симметриялы үш фазалы тізбектің кедергілері
Егер де симметриялы үш фазалы тізбектің шықпаларына кернеудің тура, кері және нөлдік реттіліктері бар токтардың симметриялы жүйесі ынта салынса, онда бұл тізбекте сол сияқты реттіліктері бар токтардың симметриялы жүйесі пайда болады. Комплексті фазалық кернеудің тура, кері және нөлдік реттіктерінің сәйкесті фазалық комплексті токтардың тура, кері және нөлдік реттіліктеріне қатынасы сәйкесті тізбектің комплексті кедергісінің тура 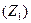 , кері
, кері 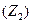 және нөлдік
және нөлдік 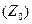 реттіліктері деп аталады.
реттіліктері деп аталады.
Кез келген симметриялы үш фазалы статикалық тізбектерде (айнымалы электр машиналар жоқ тізбектерде) ынта салынған симметриялы кернеулердің ретін тура реттіліктен кері реттілікке ауыстырса токтардың мәндері өзгермейді (оларды тек реттілігі турадан керіге өзгереді). Сондықтан мұндай тізбектер үшін тура және кері реттіліктің келергілері бірдей 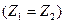 .
.
Тізбекте 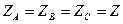 үш фазалы симметриялы тізбекті қарайық (7.5-сурет). Бұл тізбек үшін
үш фазалы симметриялы тізбекті қарайық (7.5-сурет). Бұл тізбек үшін 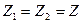 .
.
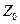 кедергінің мәнін белгілейік.
кедергінің мәнін белгілейік.

Тізбектің шықпаларына симметриялы жүйесінің фаза кернеулерінің нөлдік реттілігі 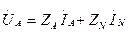 , ал содан кейін
, ал содан кейін 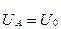 ,
, 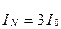 және
және 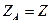 теңдеуге қойып табамыз
теңдеуге қойып табамыз 
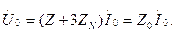 Мұндағы
Мұндағы 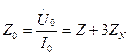 .
.
Бейтарап (нөлдік) сым жоқ кезде нөлдік реттілігі бар ток ақпайды: 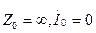 .
.
