Опр-ный интеграл как предел интегральной суммы
| Пусть дана функция y = f(x), определенная на промежутке [а,b]. Разделим промежуток [а,b] на n частей точками {xn} такими, что |
a = x0 < x1 <x2<<xn= b. На каждом промежутке [xi-1 , xi ] i=1,2 n выберем произвольным образом точку 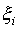 и составим сумму и составим сумму 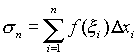 , где xi = xi ?xi-1 . Такую сумму будем называть интегральной суммой. , где xi = xi ?xi-1 . Такую сумму будем называть интегральной суммой. |
Обозначим через  , который мы будем называть диаметром разбиения. Тогда определенным интегралом от функции f(x) по промежутку [a,b] будем называть , который мы будем называть диаметром разбиения. Тогда определенным интегралом от функции f(x) по промежутку [a,b] будем называть 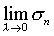 , если он существует и не зависит от способа разбиения и выбора точек , если он существует и не зависит от способа разбиения и выбора точек 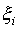 . . |
| Если такой предел существует, то функция называется интегрируемой на промежутке [a,b]. Нетрудно доказать, что если функция интегрируема, то она ограничена на этом промежутке. |
Ясно, что условие 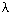 стремится к 0 может быть выполнено только, если n стремитсЯ к бесконечности,но эти условия не равносильны, так как можно увеличивать число точек деления n, оставляя один или даже несколько промежутков неизменными. стремится к 0 может быть выполнено только, если n стремитсЯ к бесконечности,но эти условия не равносильны, так как можно увеличивать число точек деления n, оставляя один или даже несколько промежутков неизменными. |
 |
Рассмотрим геометрический смысл этого определения. Для этого допустим, что  . Очевидно, что каждое слагаемое этой суммы . Очевидно, что каждое слагаемое этой суммы  равно площади прямоугольника с высотой равно площади прямоугольника с высотой 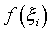 и основанием Δxi , а вся интегральная сумма и основанием Δxi , а вся интегральная сумма |
| равна площади ступенчатой фигуры, составленной из этих прямоугольников. Также очевидно, что площадь каждого прямоугольника близка к площади полосы, вырезанной из криволинейной трапеции, ограниченной графиком данной функции, осью OX и прямыми x = a и x = b, поэтому площадь ступенчатой фигуры близка к площади всей трапеции, причем, чем меньше диаметр разбиения (длина максимального основания прямоугольника), тем ближе эти площади. Таким образом, предел интегральной суммы, то есть интеграл, равен площади указанной криволинейной трапеции. |
| равна площади ступенчатой фигуры, составленной из этих прямоугольников. Также очевидно, что площадь каждого прямоугольника близка к площади полосы, вырезанной из криволинейной трапеции, ограниченной графиком данной функции, осью OX и прямыми x = a и x = b, поэтому площадь ступенчатой фигуры близка к площади всей трапеции, причем, чем меньше диаметр разбиения (длина максимального основания прямоугольника), тем ближе эти площади. Таким образом, предел интегральной суммы, то есть интеграл, равен площади указанной криволинейной трапеции. |
Формула Эйлера
Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

где e — основание натурального логарифма,
i — мнимая единица.
Доказательство формулы Эйлера основано на разложении вышеуказанных функций в ряд Тейлора:  (2)
(2)
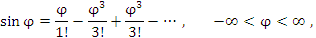 (3)
(3)
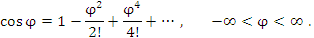 (4)
(4)
Преобразуем формулу (2), выполнив подстановку  :
:

Перегруппируем слагаемые, выделив вещественную и мнимую части:
 (6)
(6)
В соответствии с формулами(3) и (4) вещественная часть функции exp(iφ) равна cos φ, а мнимая часть этой функции равна sin φ. Следовательно,
 (7)
(7)
что и устанавливает формула Эйлера.
Формула Эйлера позволяет обобщить понятие показательной функции вещественного аргумента на случай его комплексных значений:

Св-ва опр-ного интеграла
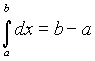 Если Если  и b > a, то и b > a, то 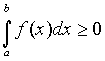 .. Если .. Если  и b > a, то и b > a, то 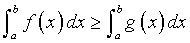   при любом расположении точек a, b и c. при любом расположении точек a, b и c. 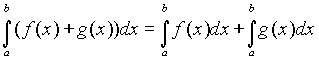  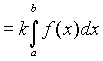 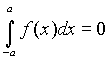 , если , если  - нечетная. - нечетная.  , если , если  - четная. - четная.  , если , если  периодическая. периодическая. |
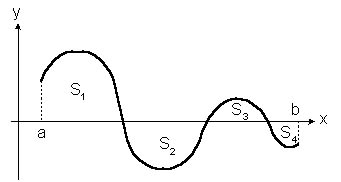 |
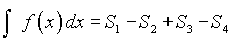 . . |
Ряды Тейлора и Маклорена
Если все производные ограничены одной и той же константой, то ряд Тейлора сходится к ф – и по x.
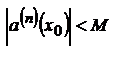
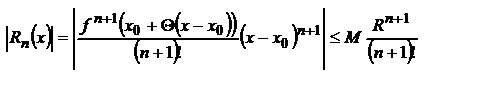
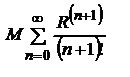 - сходится по признаку Даламбера.
- сходится по признаку Даламбера.
У сходящегося общий член ряда 
 , отсюда следует, что
, отсюда следует, что 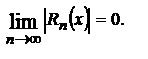
Пусть f(x) бесконечно дифференцируема и
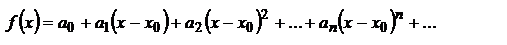 Является ли этот ряд рядом Тейлора?
Является ли этот ряд рядом Тейлора?

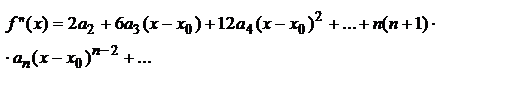 ………………………………………………………….
………………………………………………………….
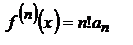 .
.
Пусть x=x0, тогда 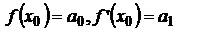 ,
,
 или
или 
f(x) – ряд Тейлора.
