Примеры решения задач типового расчёта 1 страница

Справочный материал

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числаможно пронумеровать. Эти значения случайная величина принимает с определёнными вероятностями. Число возможных значений случайной величины может быть конечным или бесконечным ((в последнем случае множество всех возможных значений называют счётным).счётным).

Законом Рядом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей:

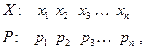
где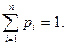

Закон Ряд распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки 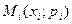и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в 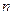независимых испытаниях, в каждом из которых вероятность появления события равна 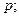вероятность возможного значения 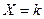(интересующее нас событие появилось 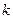раз) вычисляют по формуле Бернулли:

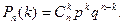
Здесь 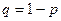- вероятность непоявления события.

Законом распределения Пуассона называется ряд распределения случайной величины Х вида

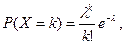
где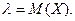

Законом Пуассона может быть приближённо заменено биномиальное распределение, когда вероятность 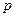появления события в каждом отдельном опыте мала, а число 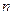производимых опытов велико. В этом случае имеет место приближённое равенство

Если число испытаний велико, а вероятность 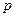появления события в каждом испытании очень мала, то используют приближённую формулу

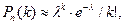
где 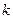- число появлений события в 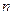независимых испытаниях, 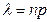- среднее число появлений события, 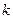- число появлений события в 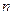независимых испытаниях в 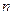испытаниях, и говорят, что случайная величина распределена по закону .Пуассона.

Математическим ожиданием (или средним) дискретной случайной величины называют сумму произведений всех её возможных значений на соответствующие им вероятности:

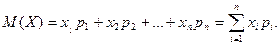
Математическое ожидание случайной величины, имеющей биномиальное распределение, биномиального распределения равно произведению числа испытаний на вероятность появления события в каждом испытании:

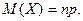
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

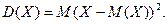
Дисперсию удобно вычислять по формуле

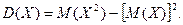
Дисперсия случайной величины, имеющей биномиальное распределение, биномиального распределения равна произведепроизведению числа испытаний на вероятности появления и непоявления события в одном испытании:

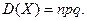
Средним квадратическим отклонением случайной величины называют квадратный корень

из дисперсии:

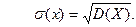
Функцией распределения или интегральной функцией распределения называют функцию

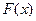, определяющую для каждого значения 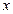вероятность того, что случайная величина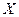

примет значение, меньшее 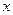, т.е.

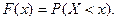
Непрерывной случайной величиной называется такая, которая может принимать любые числовые значения в заданном интервале и для которой при любом 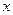из этого интервала существует предел

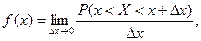
именуемый дифференциальной функцией или плотностью вероятности.

Дифференциальной функцией или плотностью вероятностей непрерывной случайной величины называют Последняя есть первуюая производнуюая от функции распределения:

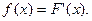
Вероятность попадания непрерывной случайной величины в интервал 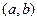определяется по формуле

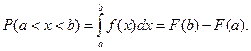
Зная плотность распределениявероятности, можно найти функцию распределения:

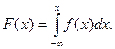
Числовые характеристики непрерывной случайной величины 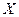, все возможные значения которой принадлежат интервалу 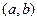, определяются по формулам

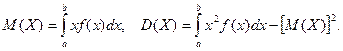
Если случайная величина 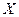имеет конечную дисперсию, то при любом 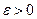справедливо неравенство Чебышева:

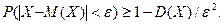
Это означает, что вероятность отклонения случайной величины 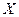от её математического ожидания по абсолютной величине меньше положительного 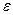, не меньше, чем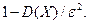

Плотность вероятности нормально распределённой случайной величины имеет вид:

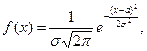
где 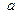- математическое ожидание, 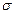- среднее квадратическое отклонение случайной величины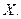

Вероятность того, что 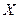примет значение, принадлежащее интервалу 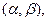определяется по формуле

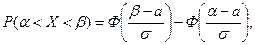
где 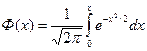- функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше положительного 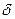, определяется по формуле

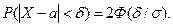
В частности, при 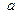=0 справедливо равенство

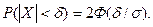
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 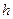, а высоты равны плотности относительной частоты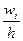 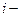го интервала. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Интервальная оценка – это оценка, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надёжностью 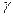покрывает оцениваемый параметр.

Интервальной оценкой с надёжностью 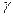математического ожидания 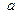нормально распределённого количественного признака 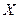по выборочной средней 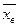при известном среднем квадратическом отклонении 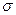генеральной совокупности служит доверительный интервал

,

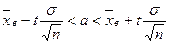где 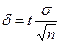- точность оценки, 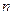- объём выборки, 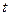- значение аргумента функции Лапласа 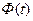(см. приложение 2), такое, что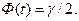

Примеры решения задач типового расчёта

Задача 1

Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения дискретной случайной величины Х – числа отказавших элементов в одном опыте. Найти числовые характеристики, интегральную функцию, построить полигон распределения.

Решение

Возможные значения случайной величины Х лежат в интервале 0…3. Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, 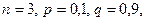получим:

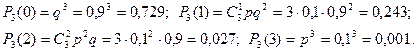
Отметим, что сумма этих вероятностей, как вероятность полной группы событий, равна 1.

Напишем искомый биномиальный закон распределения:

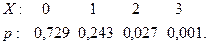
Найдём теперь числовые характеристики.

Математическое ожидание биномиально распределённой случайной величины

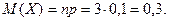
Дисперсия и среднее квадратическое отклонение

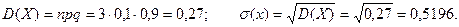
Найдём интегральную функцию

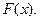
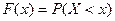- значение интегральной функции в заданной точке равно вероятности того, что случайная величина находится левее заданной точки. Тогда

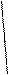
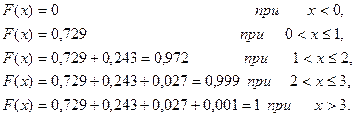F(x) график 1

0,729

X

0 1 2 3

Задача 2

1. Среднее число заказов такси, поступающих на диспетчерский пункт за одну минуту, равно трём. Найти вероятность того, что за 2 минуты поступит четыре вызова.

Решение

По условию, среднее число заказов 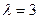, время 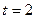, число наступлений события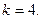

Воспользуемся формулой Пуассона

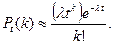
Вероятность того, что за две минуты поступит четыре вызова, равна

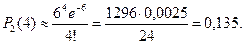
2. С базы отправили в магазин 500 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,002. Составить закон распределения дДискретнойая случайнойая величиныа Х – числао привезённых в магазин разбитых бутылок. Вычислить вероятности возможных значений Х=0,1,2,3,4. Найти числовые характеристики. Возможные значения Х принять в интервале 0…4.

Решение

Число 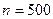велико, а вероятность 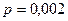мала и рассматриваемые события (повреждение бутылок) независимы, поэтому имеет место формула Пуассона

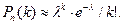
Найдём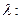

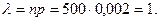
Найдём вероятность того, что Х равно нулю (нет повреждённых бутылок):

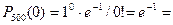0,3679.

Вероятности того, что Х примет значения 1, 2, 3 и 4, равны соответственно

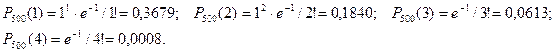
Таким образом, закон Искомый ряд распределения имеет вид:

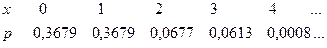
Математическое ожидание

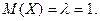
Дисперсия

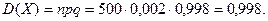
Задача 3

Вероятность появления события А в каждом испытании равна ½. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события А заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.

Решение

Найдём математическое ожидание и дисперсию дискретной случайной величины Х – числа появлений события А в 100 независимых испытаниях:

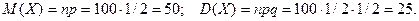
Найдём максимальную разность между заданным числом появлений события и математическим ожиданием:

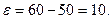
Воспользуемся неравенством Чебышева в форме

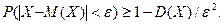
Подставляя значения 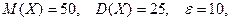получим

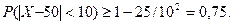
Задача 4

Дана дифференциальная функция непрерывной случайной величины Х:

. .

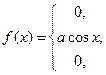
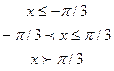Найти параметр 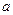, вероятность попадания случайной величины Х в интервал (- 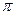/6, 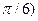, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить графики дифференциальной и интегральной функций.

Решение

Параметр 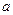найдём из условия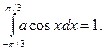

Тогда

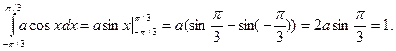
Отсюда

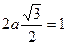и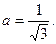

График дифференциальной функции (плотности вероятности):

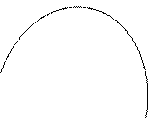
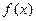
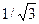
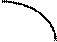
График 3

0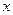

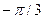
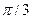
Вероятность попадания случайной величины в заданный интервал определяем как

.

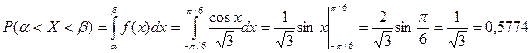Найдём математическое ожидание

.

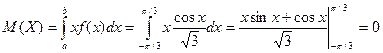Найдём дисперсию

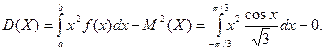
Отсюда

.

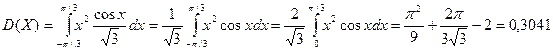Тогда среднее квадратическое отклонение

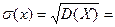0,5514.

Найдём теперь интегральную функцию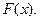

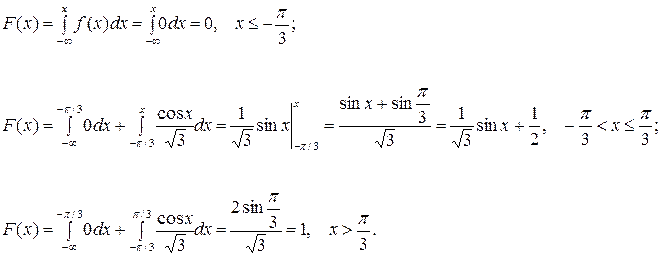
График интегральной функции:

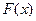
1

График 4