Из полученного результата следует, что не все корни рассматриваемого многочлена расположены в левой полуплоскости.

Предположим, что коэффициенты многочлена заданы в виде рациональной функции параметра. В этом случае система Mathematica позволяет найти область значений параметра, в которой корни рассматриваемого многочлена будут лежать в левой полуплоскости ( иначе говоря, рассматриваемый многочлен будет устойчивым).

Пример 3.4.8. Для многочлена

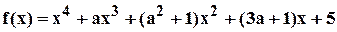
найти область устойчивости.

Решение.

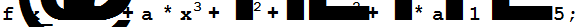
L=CoefficientList[f[x],x];

n=Length[L]

L=Reverse[L];

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],

{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

T=Table[Det[SubMatrix[GG,{1,1},{m,m}]],{m,2*n1}];

R=T[[1]]>0;Do[R=R&&T[[n]]>0,{n,2,4}]

N[Reduce[R,a]]

a>1.98271

Предположим теперь, что коэффициенты многочлена зависят от двух параметров. Рассмотрим следующий

Пример 3.4.9. Найти область устойчивости многочлена

.

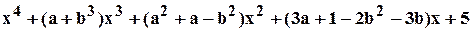Решение.

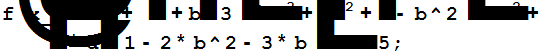
L=CoefficientList[f[x],x];

n=Length[L]

L=Reverse[L];

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],

{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

T=Table[Det[SubMatrix[GG,{1,1},{m,m}]],{m,2*n1}];

R=T[[1]]>0;Do[R=R&&T[[n]]>0,{n,2,4}]

<<Graphics`InequalityGraphics`

InequalityPlot[ R, {a, -8, 8}, {b, -8, 8} ]

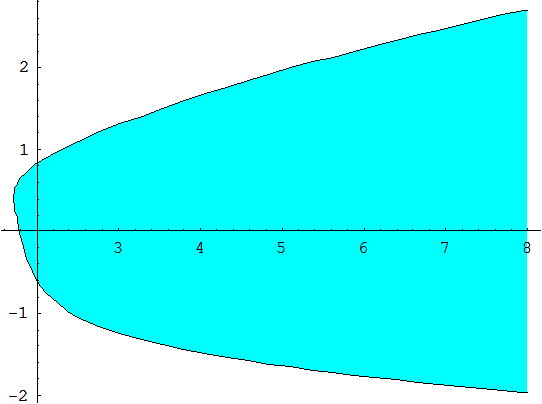
Пусть теперь коэффициенты многочлена зависят от трёх параметров. Тогда область устойчивости многочлена получается следующим образом.

Пример 3.4.10. Найти область устойчивости многочлена

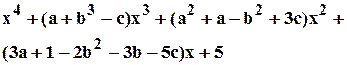
Решение.

L=CoefficientList[f[x],x];

n=Length[L]

L=Reverse[L];

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],

{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

T=Table[Det[SubMatrix[GG,{1,1},{m,m}]],{m,2*n1}];

R=T[[1]]>0;Do[R=R&&T[[n]]>0,{n,2,4}]

<<Graphics`InequalityGraphics`

InequalityPlot3D[ R, {a, -1, 1}, {b, -1, 1} ,

{c,-1,1}]

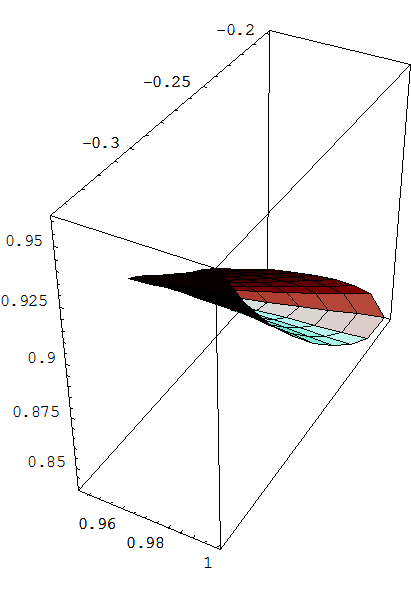
Результант и дискриминант двух многочленов.

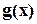Два многочлена и тогда и только тогда имеют общие корни, когда их наибольший общий делитель 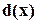отличен от нуля. В этом случае общими корнями и 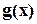являются корни их наибольшего делителя .

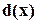Пример 3.5.1. Найти общие корни многочленов

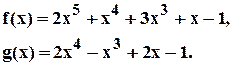
Решение. Находим наибольший общий делитель заданных многочленов и его корни.

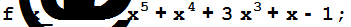
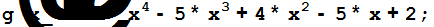
d[x_]=PolynomialGCD[g[x],f[x]]

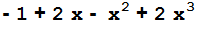
R=Solve[d[x]Š0,x];

x=x/.R;

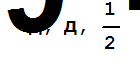
Найденные корни наибольшего общего делителя данных многочленов и являются их общими корнями.

Укажем ещё один способ, позволяющий установить наличие общих корней у двух многочленов

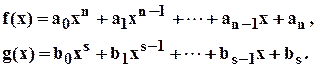(5.4.1)

Предполагается, что .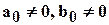

Результантом многочленов (5.4.1) называется определитель следующего вида

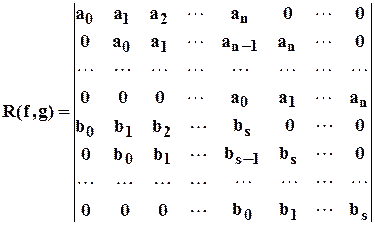(5.4.2)

Можно доказать, что результант многочленов и 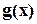равен нулю тогда и только тогда, когда эти многочлены имеют общие корни.

В системе Mathematica имеется специальная функция для вычисления результанта двух многочленов.

Пример 3.5.1. Найти результант двух многочленов

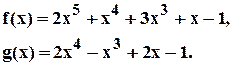
Решение.

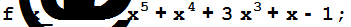
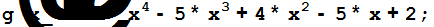
Resultant[f[x],g[x],x]

Число 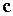тогда и только тогда является корнем многочлена , когда делится без остатка на 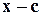. Если при этом делится без остатка на 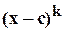, но уже не делится на 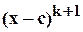, то 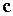называют 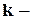кратным корнем ( или корнем кратности 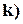рассматриваемого многочлена .

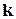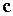Можно доказать, что если производная порядка многочлена равна нулю в точке , а производная порядка 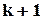отлична от нуля в этой точке, то 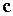является 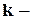кратным корнем рассматриваемого многочлена.

Из сказанного следует, что для того, чтобы проверить, имеет ли рассматриваемый многочлен корни, кратность которых больше единицы, достаточно вычислить результант многочлена и его производной.

Пример 3.5.2. Доказать, что многочлен

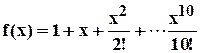
не имеет кратных корней.

Решение.

Находим результант данного многочлена и его производной.

f1[x_]=D[f[x],x];

Resultant[f[x],f1[x],x]

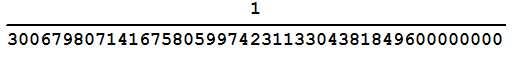
Пример 3.5.3. Найти все значения 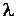, при которых многочлен

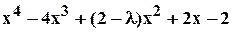
имеет кратные корни.

Решение.

f1[x_]=D[f[x],x];

R=Resultant[f[x],f1[x],x];

Solve[RŠ0,l]

Многочлены от нескольких переменных.

Многочленом 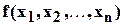от переменных 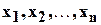над числовым полем 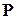7называется сумма конечного числа членов вида 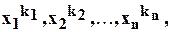где 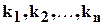- целые неотрицательные числа с коэффициентами из поля 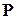. При этом предполагается, что многочлен подобных членов не содержит, и члены, с коэффициентами, равными нулю, не рассматриваются. Два многочлена 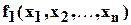и 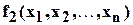считаются равными, если равны коэффициенты при одинаковых членах.

Сумма 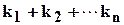называется степенью члена 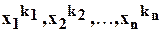многочлена 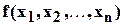. Наибольшая из этих сумм называется степенью многочлена 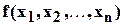по совокупности переменных. Многочлены нулевой степени- это отличные от нуля числа из поля P. Число ноль также считается многочленом. Это единственный многочлен от n переменных, степень которого не определена. Если все члены многочлена имеют по совокупности переменных одну и туже степень 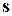, то такой многочлен называется однородным многочленом или формой 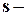й степени от n переменных.

Степенью многочлена 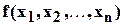по отношению к одному из переменных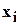 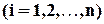называется наивысший показатель, с которым 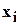входит в члены этого многочлена. Эта степень может быть и нулевой.

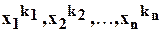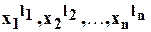Из двух членов и многочлена 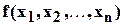считается тот выше, у которого показатель при 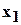больше, а если эти показатели равны, то тот, у которого показатель при 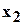больше и т.д. ( т.е. первый член выше второго, если первая из разностей 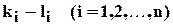, отличная от нуля, положительна) .

Если все члены многочлена расположены в таком порядке, что каждый следующий член ниже предыдущего, то говорят, что члены многочлена расположены лексикографически. Тот член, который при этом стоит на первом месте, называется высшим членом многочлена.

Суммой многочленов 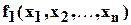и 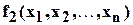называется многочлен, все коэффициенты которого получаются сложением соответствующих коэффициентов 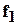и 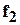. Если при этом какой-то член входит лишь один из многочленов 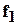и 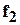, то он считается входящим и в другой многочлен с коэффициентом, равным нулю.

Произведением многочленов 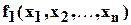и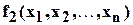

называется многочлен, полученный умножением 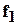на 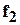с последующим приведением подобных членов. Степень (по совокупности переменных) произведения двух многочленов от переменных, отличных от нуля, равна сумме степеней этих многочленов. Высший член произведения двух многочленов равен произведению высших степеней сомножителей.

Многочлен 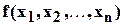от переменных называется симметрическим, если он не изменяется ни при какой перестановке этих переменных.

Симметрические многочлены от переменных

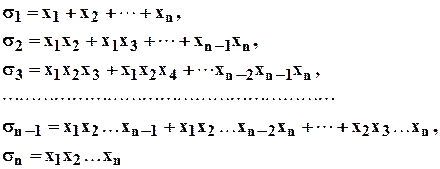(3.6.1)

называются элементарными или основными симметрическими многочленами порядка .

Пример 3.6.1. Найти основные симметрические многочлены пятого порядка.

Решение.

T=Table[Coefficient[f[x],x,n-1],{n,1,5}]

T[[4]]

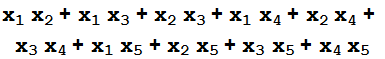
T[[5]]

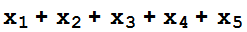
Если 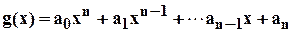- многочлен с коэффициентами из поля 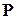, то значения элементарных симметрических многочленов от переменных при значениях переменных, равных корням многочлена 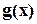соответственно равны

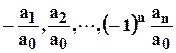. (3.6.2)

Основная теорема о симметрических многочленах формулируется следующим образом: всякий симметрический многочлен от переменных 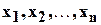можно представить в виде многочлена от основных симметрических многочленов с коэффициентами из того же числового поля, в котором лежали коэффициенты симметрического многочлена. Такое представление единственно.

Система Mathematica позволяет находить такое представление.

Пример 3.6.2. Вычислить

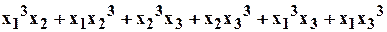
от корней уравнения .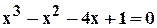

Решение.

<<Algebra`SymmetricPolynomials`