Гаусс-остроградский формуласы

Беттік интегралдар

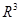-те тегіс D бетін қарастырамыз.Ол өзінің барлық нүктелерін де өзгешеленбеген деп есептейміз,яғни оның 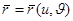,мұндағы 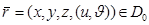параметрлік берілу кезінде оның Якоби матрицасының рангы максималды және екіге тең.Алдымен, 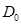облысы квадрат деп есептейік.Оның ұсақталған V бөлінуді 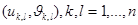таңбасымен тең 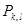квадраттарын аламыз.Мұнда 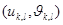нүктесі бұл 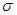қабырғасымен 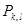квадратының сол жақ төменгі бұрышының төбесі. 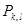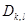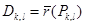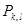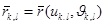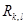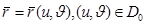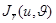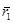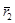квадратына сәйкес келетін D бетінің элементі- облысын қарастырамыз,яғни .Сондай- ақ , квадратына жауапты, нүктесінде D бетіне жанама жазықтықтың бөлігі- нүктелер жиынын қарастырамыз.D бетінің нүктесінде анықталған, матрицасының тиісінше бірінші және екінші бағандары болатын оған жанама екі векторлар және , яғни 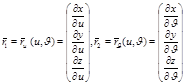.Якоби матрицасының өзгешеленбегендік шартына байланысты ,кез келген 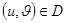нүктесі үшін 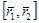векторлық көбейтіндісі нөлден өзгеше.Беттің ерекше нүктесі деп оның мынадай Якоби матрицасының рангы екіден кем нүктесін айтады.

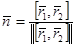векторын қарастырамыз.

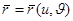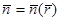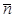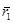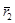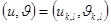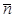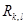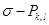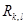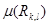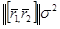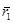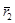Анықтама 1. параметрлеуіне жауапты,D бетіне жүргізілген нормал деп векторын айтамыз.Мұндай атау былай берілді,өйткені векторы және векторларының жанамасына перпендикуляр.Дербес жағдайда , кезінде мынаны аламыз: векторы жазықтығының жанамасына перпендикуляр.Егер квадраты қабырғасының ұзындығы болса,онда параллелограмды бейнелейді және оның ауданы - қа тең,мұндағы D векторына жанама және векторлары 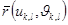нүктесінде алынған.Егер D бетінің басқа параметрлеуі берілсе,онда 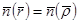немесе 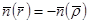теңдіктерінің бірі әрқашан орындалады.Олай болса , 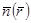және 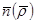векторларының скалярлық көбейтіндісіне тең 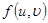функциясы бар болғаны екі мәнді +1 және -1-ді қабылдайды.Бірақ бұл функция 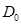-де үзіліссіз.осыдан олне +1-ге тепе-тең,не -1-ге тепе-тең.Бұл параметрлеуді алмастыру кезінде бізбен анықталған D бетіне жүргізілген нормаль D-ның барлық нүктелерінде не өзгермейтінін,не D-ның бірден барлық нүктелерінде өзінің бағытын өзгертетінін білдіреді.Сондықтан,ерекше нүктелерсіз осы тегіс беттің кейбір параметрлеуіне жауапты бетке жүргізілген нормаль онда оның қабырғасын бөледі.Бөлінген қабырғалы бетті екіжақты бет деп атайды

Анықтама 2. Параметрлеудің көмегімен D бетінің бір қабырғасын бөлу D бетін бағдарлау деп аталады.D бетінде 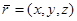үш айнымалы 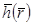функциясы берілген болсын.Ұсақталған V бөлінуге жауапты,келесі төрт интегралдық қосындыны қарастырамыз:

;

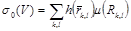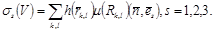
Бұдан,дербес жағдайда ,келесі өрнекті аламыз: 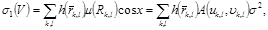мұндағы 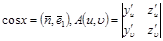. 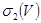және 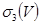үшін өрнекті осыған ұқсас жазуға болады,яғни онда cosx –ты 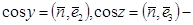ке және A= A(u,υ) -ны 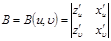, 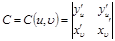ауыстырамыз. 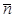нормалының векторын келесі түрде беруге болады: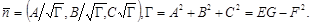

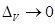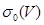Анықтама 3.Егер кезде интегралдық қосындының 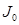шегі 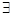, онда ол D беті бойынша 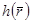функцияның бірінші текті беттік интегралы деп аталады.Осы интегралды былай белгілейді:

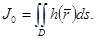
Анықтама 4.Егер 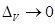кезде, 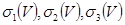интегралдық қосындыларының 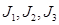шектері 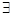, онда оларды 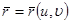параметрлеуге жауапты D бетінің қабырғасы бойынша 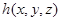функцияның екінші текті беттік интегралы деп аталады.Осы интегралдарды былай белгілейді: .

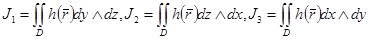Мұндағы таңбасы екінші текті беттік интегралды D жазық жиыны бойынша дағдылы қос интегралдан ажыратуды білдіреді.Бұл таңба жиі алынып тасталады. 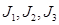интегралдарда дифференциалдық түрдің орнына мынадай түрлерді енгізуге болатынын атап өтеміз: 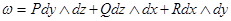және осы дифференциалдық түрдің екінші текті интегралын 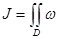қарастырамыз.Олардың анықтамасынан тікелей шығатын бірінші және екінші текті интегралдарға енгізілген екі қасиетін келтіреміз.

1)Келесі теңдік дұрыс 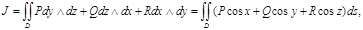мұндағы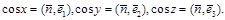

2)Теорема 1.(қос интегралға беттік интегралдың мәлімет туралы) D бетіне компактылы,Жордан бойынша өлшемді ,өзгешеленбеген (ерекше нүктелерсіз), 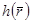функциясы тегісте үзіліссіз болсын.Онда келесі теңдіктердің орны бар:

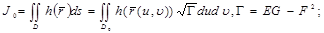
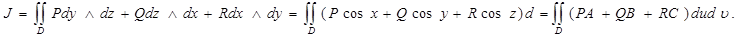Дәлелдеуі.Қисықсызықты интегралдардың айырмашылығы мұнде негізінде ештеңені дәлелдемейді,өйткені интеграл астындағы функция олардың D компактіде үзіліссіздігіне байланысты ,интегралданатын болады.Сондықтан 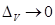кезде тиісті интегралдық қосындылар осы интегралдардың мәніне жинақталуға міндетті.Дәлелденді.

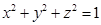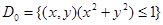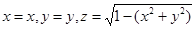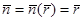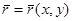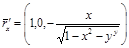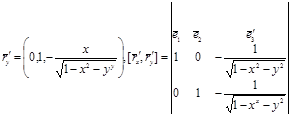
Мысал.1) D бетін ,яғни жоғарғы жарты сфераның “сыртқы келбетін” қарастырамыз.\оны дөңгелегінің бейнесі ретінде бейнелеуі кезінде беруге болады. екенін көрсетейік.Шынында да , параметрлеуі үшін мынаны аламыз: , 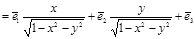.Олай болса 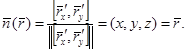Енді .

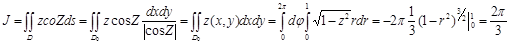Мысал . 2)D беті 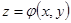теңдеуімен берілген болсын , мұндағы 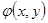- тегіс функция , 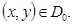Интегралдау D бетінің жоғарғы жағы бойынша жүргізіледі,яғни бұл жағдайда 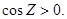Осы жағын 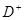арқылы белгілейміз.Сонда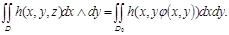

Беттің ауданы

Бет дегеніміз не? Қандай бетті қарастырамыз?Екі х және у айнымалылы кейбір g(x,y) функциясы үшін z=g(x,y) теңдеуін қанағаттандыратын (x,y,z) нүктелерінің жиынын Q бет деп атаймыз , әрі (x,y) нүктесі xOy жазықтығындағы кейбір жиынға жатады.Негізінде g(x,y) функциясынан барлық жерде үзіліссіздік талап етіледі,тек Жорданның нөлдік мөлшерінің L жиынынан басқа да болуы мүмкін.xOy жазықтығындағы Q бетінің проекциясы D облысы бойынша өлшенетін компакт деп ұйғарайық . Өлшенетін 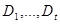жиындарының әрбіріне сәйкес шекарадағы 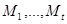нүктелерін аламыз.Жазықтықтағы проекциялар кезінде бұл нүктелерге Q бетіндегі 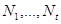нүктелері сәйкес келеді. 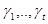бұлар 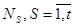нүктесінде Q бетіне жүргізілген нормаль мен Oz осі арасындағы бұрыштар болсын. 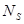нүктесі арқылы өтетін және xOy жазықтығында өзінің проекциясы болатын D облысы бар,жанама 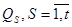жазықтығының бөлігін қарастырамыз."Қабыршақты" бетті аламыз.Сызықтық алгебрадан белгілі,оның ауданы 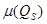мынаған тең:

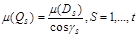
Q бетінің ауданы деп

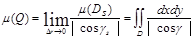
шамасын айтамыз.Беттің теңдеуінің түрі z=g(x,y) болғандықтан , Q бетінің N нүктесіндегі оның нормалін мына түрде беруге болады:

.

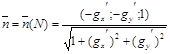Сондықтан, 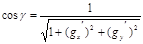аламыз .Бұдан .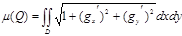

Сонымен,соншалықты қатаң емес геометриялық ұйғарымнан үшөлшемді кеңістіктегі беттің ауданының формуласын аламыз.

Анықтама 22. n-өлшемді 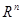-кеңістігіндегі Q бет деп мынадай 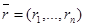, 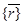нүктелері жиынын 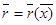,мұндағы 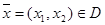айтамыз.Әрі D облысы шектелген және Жордан бойынша өлшемді 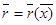бейнелеуі Q жиыны нүктелеріндегі D жиынының ішкі нүктелерінің өзара бірмәнді бейнелеуі және 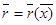жорданның нөлдік өлшемі болатын L жиынынан басқаның бәрінде үзіліссіз.Егер 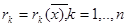функциясы үзіліссіз болса,онда 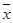нүктесінде 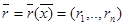бейнелеуі де үзіліссіз дербес туынды бар болса ,онда 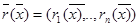бейнелеуін тегіс деп атаймыз.

Ескерту.Q бетті әртүрлі тәсілмен беруге болады.Жоғарыда көрсетілген Q беттің берілуі параметрлік (немесе Q жиынын параметрлеу ) деп аталады.Параметрлеуді таңдау да әртүрлі болуы мүмкін .Кез-келген бекітілген 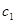және 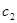мәндерінде Q-дағы 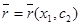және 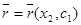түріндегі қисықтар Q бетінің қисықсызықты координатасы деп аталады. 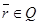нүктесінің әрбіріне қисықсызықты координатаның 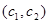жұбы сәйкес келеді.

Анықтама 23. Егер оның берілген 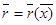бейнелеуі тегіс болса,онда Q бетін тегіс деп атаймыз.Егер 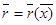бейнелеуінің Якоби матрицасының рангісі максимал яғни 2-ге тең болса,онда тегіс бетті ерекшеленбеген деп атаймыз.Өлшемді анықтауға яғни ерекшеленбеген кеңістіктегі жиындар ауданы ұғымын анықтауға ұмытыламыз.Ол үшін алдымен,жиын ауданы және өлшемі қандай қасиеттерге ие болуы керек екенін анықтауымыз керек.Өлшемнің дағдылы қасиеттерінен бөлек (монотондығы,аддитивтілігі,кеңістіктің ортогональдық тәуелділігіне қатысты инварианттылығы,параметрлеудің тәуелсіздігі) 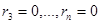жағдайында яғни "жазық" бейнелеу 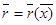үшін 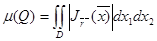формуласының болуы қажет ,мұндағы 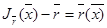бейнелеуінің Якобианы :

.

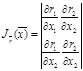Ұйғарымның қарапайымдылығы үшін , жазық D жиыны бұл тұйық шаршы деп ұйғарамыз.Онда бұл жағдайында D бейнесінің 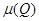өлшемі бұл D шаршысына тең 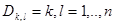шаршыларына Т бөліну үшін интегралдың 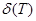қосынды 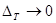кезіндегі шегі :

,

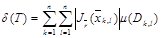Мұндағы 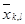бұл 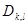шаршысының сол төменгі төбесі Q фигурасы ауданының формуласын қорыту кезінде 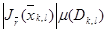саны параллелограмның ауданына тең болатынын көреміз.Онда 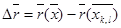бейнелеуін 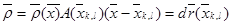түріндегі 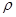сызықтық бейнелеуіне ауыстыру кезінде 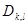шаршысына көшеді,мұндағы 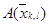бұл 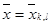нүктесіндегі 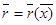бейнелеуінің Якоби матрицасы.Сонымен , 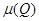есептеу кезінде біз 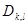шаршыларына D бөлінуін аламыз,ал содан соң әрбір 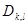шаршысы үшін 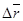бейнелеуін 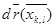сызықты бейнелеуімен алмастырамыз.Мұндай алмастыру кезінде , бейненің ауданы неге тең болады? Барлық 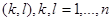жұптары бойынша алынған аудандардың қосындысы 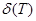интегралдық қосындысын береді.

Сол нобайды Q бетінің ауданы анықтамасының негізіне қойсақ және жалпы жағдайда яғни Д шаршының Т бөлінуін тең 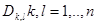шаршыларымен алу керек.Содан соң , 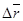бейнелеуін 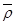сызықты бейнелеуіне алмастырсақ

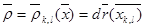
және 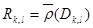өлшемін қосамыз.Сонда

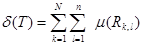
аламыз.

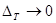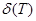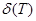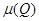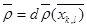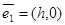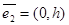Анықтама 24. Егер кезінде шегі бар болса,онда бұл шекті Q бетінің ауданы деп атаймыз.Енді шамасын есептеу және оның шегін табу ғана қалды.Ол үшін бейнелеуі кезінде және векторлары

,

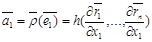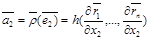
векторларына көшеді.Векторлар 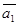және 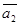-ден құрылған параллелограмның ауданын табу керек.Ол үшін сызықты алгебраның формуласын қолданамыз,яғни ол келесіні тұжырымдайды:

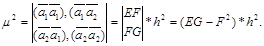
Осы формуланың қарапайым қорытындысын келтірейік.Векторлар 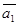және 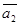-ден құрылған параллелограмм ауданының формуласының түрі мынадай болады:

.

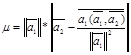Осы формуланы түрлендірейік.Сонда :

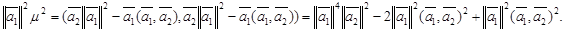
Олай болса,

.

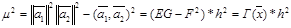Сонымен , мынаны аламыз:

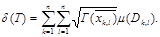
Функция 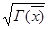D-да үзіліссіз,сондықтан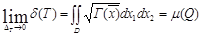

шегі табылады.Басқаша айтқанда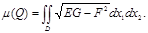

Соңғы интегралдың меншікті де,меншіксіз де болуы мүмкін екенін байқаймыз.Қабырғалары 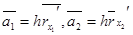болатын параллелограмның ауданы :

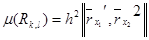
тең.Бұдан беттің ауданы үшін формуланы аламыз:

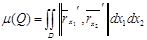
Мысалы 1. Жоғары жарты сфераның 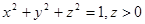бетінің ауданы 2 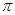-ге тең.

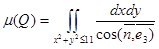мұндағы 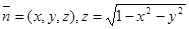.Олай болса,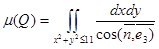

Полярлық координатаға көшеміз :

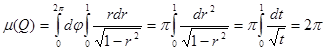
2)Екі өлшемді тордың ауданы Д облысында 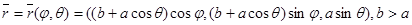параметрді өзгерту теңдеуімен берілген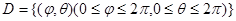

Сонда ,

,

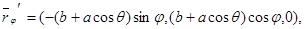
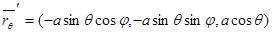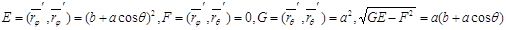
Бұдан мынаны аламыз:

Векторлық өрістің дивергенциясы және роторы

Гаусс-Остроградский формуласы

Бұл фомула үш өлшемді кеңістіктегі Грин формуласының аналогы болады.

Т5. (Гаусс-Остоградский формуласы)

1) 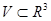жиыны-дөңес, Жордан бойынша өлшемді, компактылы.

2)V жиының S шекарасы-өзгешеленбеген (ерекше нүктелерсіз) бөліктік – тегіс кеңістік ;

3) V жиынындағы 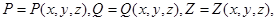тегіс функциялар берілген. Онда мына формуланың орны бар: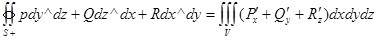

Мұнда теңдіктің сол бөлігінің интегралы 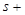бетінің сыртқы жағы бойынша алынатын екінші текті интеграл, ал теңдіктің оң бөлігі - 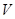жиыны бойынша кәдімгі үш еселі интеграл. Дәлелдеуі. Грин формуласын дәлелдеу кезіндегідей, 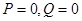жағдайын қарастрамыз. 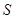бетін 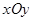жазықтығына проекциялап және Д арқылы бұл проекцияны белгілейміз. 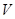-ның дөңестігіне байланысты, 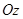осіне параллель және Д-ны өиятын әрбір түзу кесінді бойынша 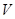-ны қияды. 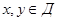болсын, онда осы кесіндінің төменгі шетінің координаты 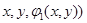, ал кесіндінің жоғарғы шетінің координаттары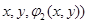 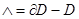облысының шекарасын білдіретін болсын. Сонда Д беті үз бөліктік-тегіс бөлікке бөлінеді.

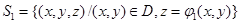
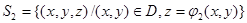
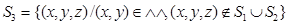
Мұнда 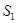беті үшін интегралдау оның төменгі жағы , соңында 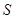бетінің бүйір бөлігін біліретін 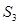беті үшін, 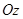осіне перпендикуляр нормаль жағы бойынша жүргізіледі және Д-ға қатысы бойынша сыртқы нормалі болады. Беттік интегралды Риман қос интегралына келтіру туралы теорема бойынша мынаны аламыз:

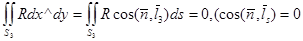Одан әрі

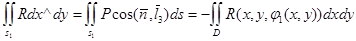
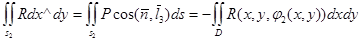
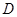
Бекітілген 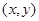кезінде Ньютон-Лейбниц формуласы бойынша мынаны аламыз: .

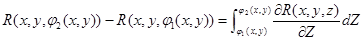Олай болса, 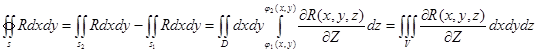Дәлелденді.

Мысал: 1) Т1 ден 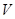денесінің көлемі үшін келесі өрнекті 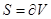беті бойынша беттік интеграл арқылы аламыз: 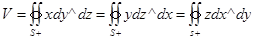Мұнда беттік интегралдар беттің сыртқы жағы бойынша алынады. беттің сыртқы жағын анықтау үшін оған беттің нүктесі және дөңес денесінің 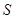бетіне сыртқы нормаль бағыты ретінде алсақ , онда берілген нүктенің төбесінен 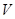денесінің басқа нүктелерін қамтымайтын осы түзудің сәулесінің бағыты арқылы нормаль түзу жүргізу керек.

2) (Гаусс интегралы) 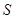бөліктік- тегіс, өзгешеленбеген , Жордан бойынша өлшемді, компакт бет болсын. 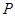-кейбір бекітілген нүкте, 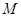-бет 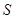теі айнымалы нүкте , 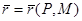-бастапқы 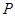нүктесі және соңғы 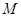нүктесінің радиус векторы 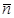- 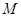нұктесіндегі бетке жүргізілген сыртқы нормаль болсын. Сонда мынаны аламыз:

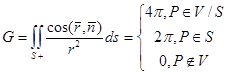
Алдымен, 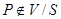нүктесі жағдайын қарастырамыз. 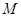нүктесінің координатасы 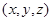, ал Р нүктесінің координатасы 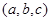болсын. Сонда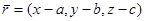 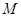нүктесіндегі бетке жүргізілген нормаль векторы 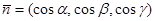-ға тең. Олай болса,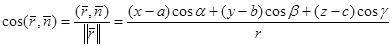

Гаусс-Остоградский формуласын қолданып, мынаны аламыз.

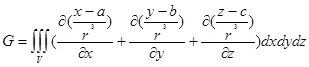
Сонда,

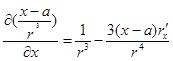
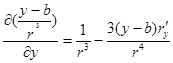
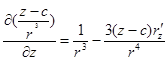
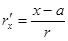
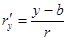
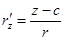
Олай болса,

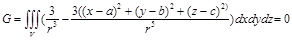
Егер 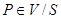нүктесі болса , онда оны түгелімен 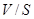-тің ішінде жататын 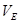шарымен қоршаймыз. Осы шардың бетін 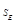арқылы белгілейміз . Алдыңғыға байланысты мынаны аламыз:

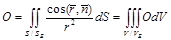бірақ теңдіктің орны бар болғандықтан , символдық түрде былай жазамыз:

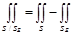онда, теңдікке байланысты 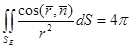мынаны аламыз: 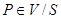жағдайында G интегралының мәні 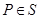жағдайы да қарастырылады.

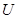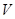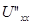
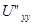
3)(Грин формуласы)Гаусс-Остоградский формуласының тамаша салдары ретінде математикалық физикада қолданылатын тағы бір грин формуласын қарастырамыз. және -үзіліссіз 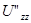екінші дербес туындылары бар тегіс функциялар болсын. Сондай-ақ 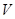дөңес , Жордан бойынша өлшемді, 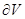шекарасымен компакт бөліктік –тегіс бағдарланған бет болсын. Одан басқа 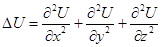Лаплас операторы, 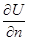бет 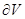-ға жүргізілген сыртқы нормальдың бағыты бойынша туындысы болсын. Сонда келесі грин формуласы дұрыс: 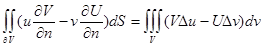шынында да , Гаусс-Остоградский формуласы бойынша мынаны аламыз : 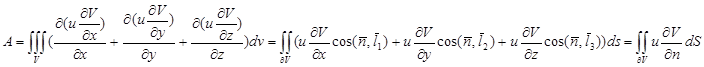Сонда

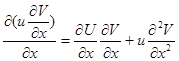
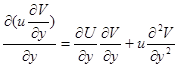
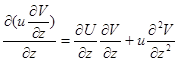
А формуласы үшін алынғанды қолданып, мынаны табамыз:

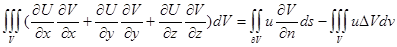
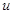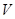Соңғы формуладағы және функцияларының орындарын ауыстырамыз. Теңдіктің сол бөлігі осындай ауыстыру кезінде өзгермейді. Олай болса , оң бөлікте тұрған өрнектің де мәні өзгермейді. Ал бұл келесі теңдікті береді: 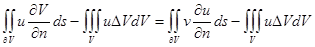, яғни

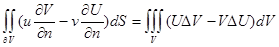Соңғы формуланы грин формуласы деп атайды. Ол гармоникалық функцияларды зерттеу кезінде өте пайдалы, яғни 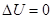Лаплас теңдеуің қанағаттандыратын функция.

Грин формуласы

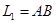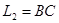Екінші текті интегралдың аддитивтілігіне байланысты кез келген және қисықтары үшін 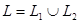қисығының еселі нүктелері болмаған жағдайда , мынаны аламыз: .

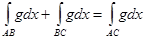Осы формула бойынша А және С нүктелері беттескен жағдайда L қисығы бойынша интеграл анықталады .Бұл жағдайда 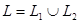қисықтарының бірігуі тұйықталған қисық деп аталады .

Анықтама 28.Егер

1) ;

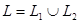2) 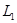және - 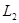шеттері беттесетін бөлікті-тегіс қисықтар;

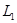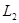3) және қисықтарының басқа жалпы нүктесі болмасада , онда қисық , тұйық бөлікті – тегіс қисық (еселі нүктелерсіз) деп аталады . Егер 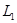қисығында айналып өту бағыты берілсе , яғни бастапқы А нүктесі және соңғы В нүктесі берілсе ,және егер 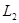қисығында бастапқы нүкте ретінде В , ал соңғысы ретінде А нүктесін алсақ , онда L қисығында кез келген үш әртүрлі 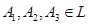нүктелері үшін әрқашанда келесі нүктелермен жүру ретінің 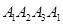немесе 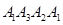біреуінің орны бар мағынасындағы айналып өту бағыты беріледі . Сондықтан кез келген тұйық L қисықта дәл екі айналып өту бағыты болады , оның бірін әрине оң , ал екіншісін теріс деп есептеу керек .

Сезгеніміздей , сонымен 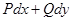дифференциалдық форманың J интегралы үшін оң бағытта алынған , тұйық L қисығы бойынша мынадай белгілеу қолданылады .

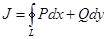Тұйық қисықты айналып өтудің оң бағытын қалай таңдауға болатынын анықтайық.Алдымен h шеңбердің 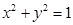маңызды мысалын қарастырамыз. Шеңберді айналып өтудің оң бағыты ретінде “сағат тіліне қарсы айналу бағыты” алынады . Ол былай анықталады . Шеңберді жоғарғы жарты шеңбер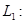 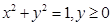және төменгі жарты шеңбер 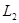-ге бөлеміз . Жоғарғы жарты шеңбердің санақ басы ретінде (1,0) координатасы мен А нүктесін аламыз және В нүктесін соңғы нүктесі деп есептейміз . Төменгі жарты шеңбер 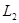-нің бастапқы нүктесі ретінде В аламыз , ал соңғы нүктесі деп А нүктесін есептейміз . Шеңбер L-ге онда А нүктесінде кез келген еркін алынған жанама 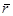векторды көрсетіп , бірмәнді айналып өту бағытын беруге болады . 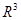кеңістігінің хОу жазықтығында L шеңберді қарастырамыз . Оның әрбір нүктесінде хОу жазықтығында жататын шеңберге жүргізілген сыртқы нормалдың векторы n̅ , оған жүргізілген жанама вектор 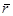берілген болсын. Егерде Oz осі бойынша бағытталған е̅₃ орты 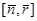векторлық көбейтіндімен беттессе , онда вектор 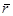шеңбер L-дің айналып өту бағытын береді деп айтамыз . Шеңбердің осы қасиетін жалпы қисық L-дің айналып өтудің оң бағытының анықтамасы негізінде аламыз .

Анықтама 29 . хОу жазықтығындағы дөңес Д жиынының шекарасы болатын еселі нүктелерсіз тұйық бөлікті-тегіс L қисығы болсын . 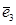Оz осі бойынша бағытталған орт болсын . L қисықтың әрбір нүктесіне жанама r̅ вектормен сыртқы нормалдың n̅ векторын береміз . Егер е̅₃ векторы 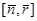векторлық көбейтіндісімен беттессе , онда L қисығында айналып өтудің оң бағыты берілген деп айтамыз . Мақсатымыз ,D облысының шекарасы болатын 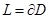тұйық қисығы бойынша қисықсызықты интегралмен осы облыс бойынша қос интеграл арасындағы байланысты тағайындайтын Грин формуласын дәлелдейміз.Қарапайымдылық үшін дөңес D облысы жағдайын қарастырамыз.

Теорема 28.(Грин формуласы)

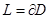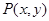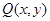D дөңес ,Жордан бойынша өлшемді,компакт,тұйық ерекшеленбеген бөлікті-тегіс қисықтың шекарасы болсын.Сол сияқты және функциялары D-да үзіліссіз және сонда үзіліссіз дербес 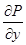және 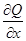туындысы бар болсын.Онда келесі формула дұрыс:

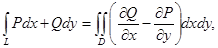мұндағы L қисығы оң бағытта айналып өтеді.Дәлелдеуі.Тек 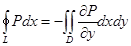теңдігін дәлелдеу керек.Осыған ұқсас 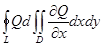теңдігі дедәлелденеді.Кесінді [a,b] Ox осіндегі D облысының проекциясы болсын.Нүктелер (а,0) және (в,0)арқылы вертикал x= ажәне x=b түзулерін жүргіземіз.D жи ын ының дөңестігіне қарай оның 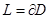шекарасы төрт бөлікке бөлінеді:x = a және x=bтүзулерінде жататын 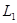және 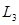кесінділері (олардың әрқайсысы тек,бір нүктеден тұруы мүмкін және осы қисықтардың арасындағы жолақта жататын 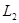және 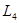қисықтары. 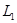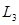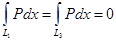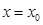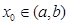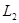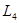және қисықтарында ч шамасы тұрақты,сондықтан .Кез келген түзуі кезінде (D-ның дөңестігіне қарай) және қисықтарының әрқайсысын қатаң түрде бір нүктеде қиып өтеді.Оларды тиісінш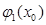е және 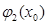арқылы белгілейміз,яғни 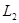қисығы 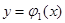функциясының графигі ,ал 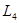қисығы 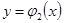функциясының графигі болады.

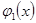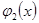Қисық L-дің бөліктік тегістігінен және функцияларының бөлікті – тегістігі шығады.Қисықсызықты интегралды Риман интегралы арқылы өрнектелуі туралы теоремадан мынаны аламыз:

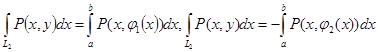
Бұдан

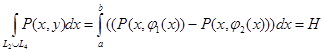
шығады.D - да 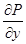функциясы үзіліссіз болғандықтан ,Ньютон – Лейбниц теоремасы бойынша:

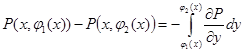аламыз.Демек,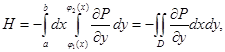 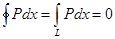қарай, 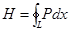формуласы дұрыс.

Грин формуласы интегралының аддитивтілігіне қарай дөңес облыстардың шектеулі бірігуі болатын облыстар үшін дұрыс екенін ескереміз.

Мысал.

1)Грин формуласына сәйкес D облысының ауданы қисықсызықты интеграл арқылы келесі түрде өрнектеледі:

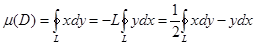
2) 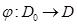екі жазық облыстың тегіс өзара бірмәнді бейнелеуі болсын.Сондай – ақ 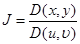бейнелеуінің якобианы 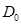облысында таңьасын өзгертпейтін және 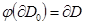болсын.Сонымен бірге, -де 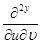үзіліссіз болсын.Сонда (1) мысалдың формуласынан шығарып,D облысының өлшемді есептеуін жүргіземіз: .

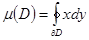қисығының 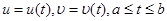түріндегі параметрлеуі берілген болсын.Сонда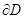

Қисығының сәйкес параметрлеуі 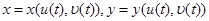теңдеуімен беріледі.

Қисықсызықты интегралдың Риман интегралы арқылы өрнектеуінен мынаны аламыз:

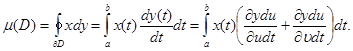
Бірақ соңғы интегралды қисығы бойынша интеграл ретінде беруге болады:яғни

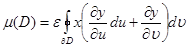мұндағы 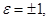егер және 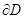қисықтарының айналып өту бағыты бірдей болса,ал 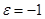қарсы жағдайда .Соңғы интегралды түрлендіріп ,Грин формуласын қолданып,мынаны аламыз:

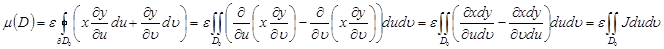Якобиан J таңбасын өзгертпейтін және 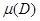шамасы теріс емес болғандықтан,онда 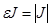.Сондықтан , 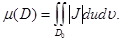Сонымен жазық облыстың ауданын қисықсызықты координатада есептеу үшін формула алынды.

Дарбу қосындысы