Основные теоремы пространственной системы сил

Приведем без доказательств формулировки основных теорем пространственной системы сил.

Теорема о параллельном переносе силы.

При параллельном переносе силы для выполнения эквивалентности необходимо добавить векторный момент переносимой силы относительно точки переноса.

Теорема о приведении пространственной системы сил к главному вектору и главному векторному моменту

Пространственную систему сил можно заменить силой, приложенной к произвольно выбранной точке (т. О) и равной главному вектору 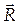₀ этой системы сил и парой сил с моментом, равным главному векторному моменту 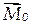системы сил относительно точки О.

Условия равновесия пространственной системы

· Произвольная пространственная система сил

Условия равновесия произвольной пространственной системы сил можно сформулировать в векторном виде:

,

(1.44)

или: пространственная система сил, у которой главный вектор и главный момент равны нулю, находится в равновесии.

Формулировка этих условий в скалярном виде выглядит так:

В условиях равновесия суммы проекций всех сил на каждую из трех ортогональных осей произвольной пространственной системы координат и суммы осевых моментов всех сил относительно каждой из этих осей, равны нулю.

Математически эти условия выражаются формулами:

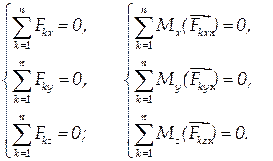(1.45)

· Пространственная система параллельных сил

Если направить одну ось (например, ось 0z) вдоль линий действия системы параллельных сил, то система уравнений равновесия сократится до трех уравнений и приобретет следующий вид:

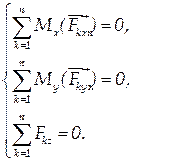(1.46)

· Пространственная система сходящихся сил

Взяв в качестве начала отсчета центр сходящихся сил, легко убедиться, что моментные уравнения в условиях равновесия превратятся в тождества, а я самой системе останутся только три уравнения проекций сил на оси координат:

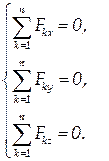(1.47)

Теорема Вариньона о векторном моменте равнодействующей силы

Векторный момент равнодействующей пространственной системы сил равен сумме векторных моментов сил системы относительно одной и той же точки.

.

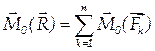(1.48)

Доказывается это утверждение аналогично доказательству соответствующей теоремы в плоской статике.

В соответствии с аксиомой статики 2, при добавлении к системе сил 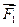, ,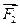..., 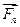с равнодействующей 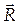уравновешивающей силы 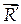тело будет находиться в равновесии. Уравнение моментов в условиях равновесия примет вид:

.

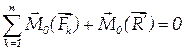Учитывая, что 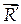= - 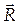, и обе силы имеют общую линию действия, то:

.

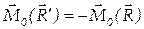Вычитая второе уравнение из первого, найдем:

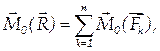
что и требовалось доказать.

Теорема о приведении пространственной системы сил к главному вектору и главному векторному моменту

Используя теорему о параллельном переносе силы, можно привести любую пространственную систему сил к главному вектору и паре сил с моментом, равным главному векторному моменту.

Пространственную систему сил можно заменить силой, приложенной к произвольно выбранной точке (т. О) и равной главному вектору 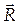₀этой системы сил и парой сил с моментом, равным главному векторному моменту 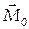системы сил относительно точки О.(см. рис.1.40).

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Сформулируйте условия равновесия для пространственной системы сил.

2. Чем отличаются условия равновесия для пространственной системы параллельных сил от условий равновесия для пространственной системы сходящихся сил?

3. Как найти векторный момент равнодействующей в данной системе сил?

[1] Впредь в тексте любой выделенный жирным шрифтомотдельный алгебраический символ следует воспринимать как векторную величину.

[2] Единицей измерения силы в системе единиц СИ является Ньютон (Н); применяется и более крупная единица 1 кН=1000Н)

[3] Ортом вектора называется единичный вектор, направленный в ту же сторону и приложенный в той же точке, что и заданный вектор.

[4] Это следствие, также как и часть аксиом и теорем статики, применимо только для абсолютно твердого, не деформируемого тела.

[5] Сила реакции, или реакция связи – сила, с которой данная связь действует на тело.

[6] См. сноску ⁴.

[7] статически определимой задача статики называется, если число неизвестных компонентов реакций равно числу уравнений равновесия, и наоборот, задача статики называется статически неопределимой, если число неизвестных компонентов реакций больше числа уравнений равновесия.