Этап. Нахождение существенных импликант. 4 страница



 x5 x5
x5 x5
 | x4 |  | x4 | |||||||||||||||||
 |  | x3 |   |  |  |  | 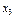 | |||||||||||||
 |  1 1 |  1 1 |  |  |  |   |  | |||||||||||||
 |  | |||||||||||||||||||
 | ||||||||||||||||||||
 |  | |||||||||||||||||||
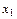 | 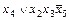 | 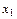 | 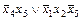 |
7 абсолютно минимальные представления
Задача о нахождении такого аналитического представления ФАЛ, при котором число букв в представлении минимально в классе ДНФ, может быть решена с использованием скобочного представления ФАЛ.
Определение 7-1. Q представляет собой минимальное представление для функции f, если не существует в базисе {-, &, 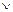 } представления более минимального , чем Q, каким бы способом ни получилось это выражение.
} представления более минимального , чем Q, каким бы способом ни получилось это выражение.
Дальнейшая минимизация МДНФ за счет вынесения за скобки является практически наиболее подходящим приемом получения абсолютно минимального представления ФАЛ в классе ДНФ.
Пример 7. Для функции
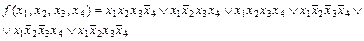
найдена МДНФ вида:
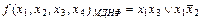 .
.
Если вынести за скобки x1, то получим абсолютно минимальное представление:
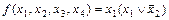 .
.
Как видим, полученное выражение содержит 3 буквы вместо четырех и, следовательно, является более простым, чем МДНФ исходной функции.
ГЛАВА 2.ПРЕОБРАЗОВАНИЯ И МИНИМИЗАЦИЯ В БАЗИСЕ СОСТОЯЩЕМ ИЗ ФУНКЦИИ ВЕББА ИЛИ ИЗ ФУНКЦИИ ШЕФФЕРА.[†]
Проблема минимизации ФАЛ может быть сформирована и для случая любого другого базиса. Функции Вебба (Пирса) и Шеффера образуют базисы, состоящие только из одной функции. Будем называть такие Базисы многофункциональными.
В последнее время возник большой интерес к многофункциональным базисам. Поэтому рассмотрим их более подробно. Оба базиса обладают одинаковыми свойствами, поэтому рассмотрим задачу минимизации ФАЛ лишь для одного из них – базиса из функции Вебба. Для упрощения записи в дальнейшем будем использовать знак  (стрелка Пирса) для обозначения функции Вебба (о).
(стрелка Пирса) для обозначения функции Вебба (о).
Все сказанное о базисе Вебба практически без всяких изменений может быть использовано и для базиса, состоящего из функции Шеффера.
По аналогии с двуместными, введем с помощью таблицы n-местные функции Вебба и Шеффера.
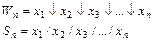
| x1 | x2 | x3 | . | . | . | xn-1 | Xn | Wn | Sn |
| . | . | . | |||||||
| . | . | . | |||||||
| . | . | . | |||||||
| - | - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - | - |
| . | . | . | |||||||
| . | . | . | |||||||
| . | . | . |
При n=2 из этой таблицы получаются двухместные функции Вебба и Шеффера, а при n=1 обе функции вырождаются в функцию отрицания. Поэтому в дальнейшем будем вместо 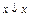 и x/x писать соответственно
и x/x писать соответственно 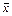 .
.
Для введенных функций справедлив переместительный закон и несправедлив сочетательный закон.
Можно записать следующие справедливые соотношения:
|
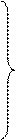
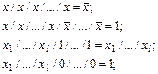
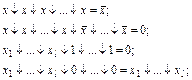
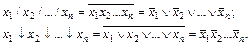
При раскрытии скобок получим:
|
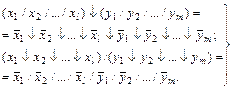
Заметим, что если l или m равны еденице, то эти соотношения выразятся несколько иначе. Например при l=1
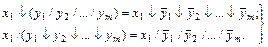 (2-3)
(2-3)
Наконец, приведем соотношения, показывающие связь между многоместными функциями Вебба и Шеффера и являющиеся аналогами формул де Моргана:
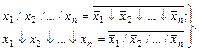 (2-4).
(2-4).
Справедливость всех вышеприведенных соотношений можно установить при помощи таблиц истинности ФАЛ.
В дальнейшем в основном будем рассматривать базис, построенный на основе многоместной функции Вебба.
Известно [11], что любую ФАЛ можно представить:
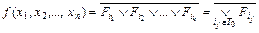 ,
,
если выбрать характеристические функции единицы для множества Т0 номеров наборов, на которых функция обращается в нуль. Применяя последнее из соотношений (2-1), получаем одну из двух совершенных нормальных форм в базисе Вебба:
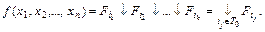 (2-5)
(2-5)
Если использовать характеристические функции единицы для множества T1 , то получится другая совершенная нормальная форма, которая проще предыдущей, если у функции в таблице истинности нулей больше чем единиц:
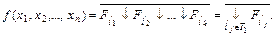 (2-6)
(2-6)
Если f обращается в нуль только на одном наборе, то в правой части (2-5) останется только один инвертированный операнд. Если же f обращается в единицу только на одном наборе, то отрицание в правой части соотношения (2-6) исчезает.
Для получения аналогичных нормальных форм в базисе Шеффера можно использовать характеристические функции нуля.
Перейдем теперь к аналитическому выражению характеристических функций единицы в базисе Вебба. Для любой характеристической функции единицы в базисе {-, &, 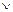 } может быть получено выражение через конституенту единицы:
} может быть получено выражение через конституенту единицы:
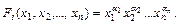
Если применить последнее из соотношений (2-1), то
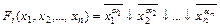
и мы можем написать что
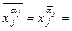
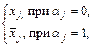
и получить выражение для характеристической функции единицы:
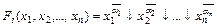 (2-7)
(2-7)
при условии, что
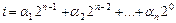
Теперь мы можем сформулировать алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы вбазисе n-местной функции Вебба вида, например, (2-5):
1. Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в нуль.
2. Выписать термы типа (2-7), соответствующие этим наборам аргументов. При этом, если аргумент 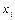 входит в данный набор как нуль, он вписывается без изменения. Если же
входит в данный набор как нуль, он вписывается без изменения. Если же 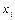 входит в данный набор как единица, то вписывается его отрицание.
входит в данный набор как единица, то вписывается его отрицание.
3. Все полученные выражения характеристических функций объединяются k-местной операцией Вебба, где k – количество нулей заданной функции.
Пример 2-1. Построить совершенную нормальную форму вида (2-5) для следующей таблично заданной функции:
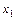 | 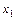 | 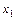 | 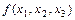 | 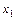 | 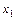 | 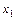 | 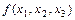 |
в соответствии с алгоритмом получаем:
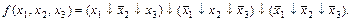
Перейдем теперь к проблеме минимизации в монофункциональных базисах. Существует два подхода к проблеме минимизации: либо по аналогии с минимизацией в классе ДНФ строится специальный метод минимизации для монофункционального базиса, либо минимизация производится в классе ДНФ, а затем строится специальный метод перехода от базиса конъюнкция, дизъюнкция, отрицание к монофункциональному базису. Рассмотрим сначала первый подход на примере минимизации в базисе , состоящем из функции Вебба.
Все определения для ФАЛ, в базисе {-, &, 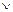 } введенные в главе 1, имеют свои аналоги и для рассматриваемого базиса. Совершенной нормальной формой в дальнейшем будем считать выражение (2-5), операнды которого будут иметь наибольший возможный для данной функции ранг. Определение минимальной нормальной формы вполне аналогично определению МДНФ в классе ДНФ.
} введенные в главе 1, имеют свои аналоги и для рассматриваемого базиса. Совершенной нормальной формой в дальнейшем будем считать выражение (2-5), операнды которого будут иметь наибольший возможный для данной функции ранг. Определение минимальной нормальной формы вполне аналогично определению МДНФ в классе ДНФ.
Понятиям интервал и максимальный интервал из геометрической интерпретации области определения функции алгебры логики соответствовали понятия импликанта и простая импликанта при минимизации в классе ДНФ. В базисе Вебба соответствующие понятия будем называть инверсантой и простой инверсантой .
Инверсанта и функции f характеризуется тем, что всегда из и=1 следует f=0. Очевидно, что все Fi из (2-5) являются инверсантами заданной функции f. Отметим, что 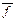 тоже является инверсантой функции f.
тоже является инверсантой функции f.
По аналогии с классическим базисом будем говорить, что выражение в базисе Вебба, операндами которого являются все простые инверсанты заданной функции, является сокращенной нормальной формой функции. Минимальная нормальная форма будет получаться из сокращенной выбрасыванием некоторых инверсантов. Определение тупиковой формы в рассматриваемом базисе формулируется по аналогии с определением из базиса {-, &, 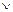 }.
}.
Прежде чем перейти к рассмотрению применения в базисе Вебба некоторых известных из классического базиса методов минимизации, рассмотрим эквивалентные преобразования, приводящие к операциям склеивания и поглощения в алгебре Вебба.
Через Zn будем обозначать выражение, которое описывает n-местную операцию Вебба над n операндами.
Лемма.Если 1<k<n, то 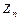 эквивалентно
эквивалентно 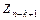 ,которое получается из
,которое получается из 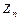 объединением в одном операнде любых k операндов с помощью введения общего для них отрицания.
объединением в одном операнде любых k операндов с помощью введения общего для них отрицания.
Другими словами,
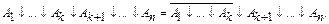 (2-8)
(2-8)
где 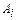 – произвольные термы и 1<k<n.
– произвольные термы и 1<k<n.
Введем теперь операции следующих типов:
Склеивания
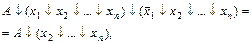 (2-9)
(2-9)
Неполного склеивания
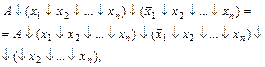 (2-10)
(2-10)
И поглощения
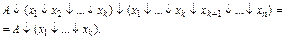 (2-11)
(2-11)
В этих выражениях включен произвольный терм A, указывающий на то, что операции производятся между операндами внутри многоместного терма. Отсутствие А привело бы к двухместным операциям и к вырождению некоторых операндов.
Для двухместного случая аналоги операций склеивания и поглощения имеют вид:
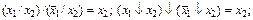 (2-12)
(2-12)
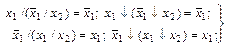 (2-13)
(2-13)
Справедливость всех этих соотношений легко доказать, построив таблицу истинности ФАЛ.
Рассмотрим теперь аналоги методов минимизации, рассмотренных нами для базиса конъюнкция, дизъюнкция, отрицание.
