Основные теоретические сведения. Определение. Производной функции f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента
Определение. Производной функции f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю. Обозначается f’(x).
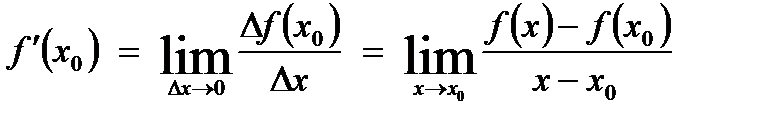
Операция нахождения производной называется дифференцированием функции.
Геометрический смысл производной: производная функции в точке хо равна угловому коэффициенту касательной, проведённой к графику данной функции в данной точке.
Механический смысл производной: мгновенная скорость прямолинейного движения материальной точки в любой момент времени есть производная от пути по времени: 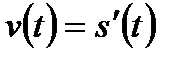
Правила дифференцирования:
1) 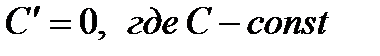 , 2)
, 2) 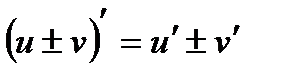 , 3)
, 3) 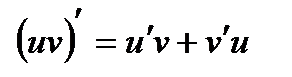 , 4)
, 4) 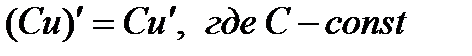 , 5)
, 5) 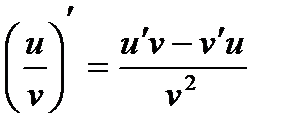 , 6)
, 6) 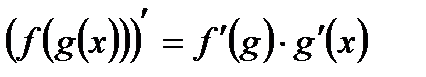 .
.
Таблица производных
(xn)′ = n·xn-1
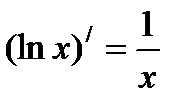
(sin x)′ = cos x
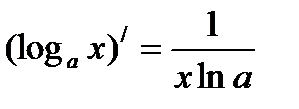
(cos x)′ = – sinх
(ex)′ = ex
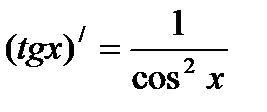
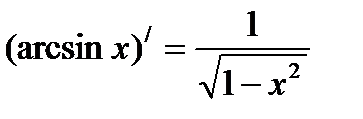
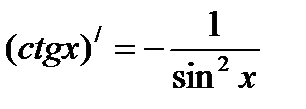
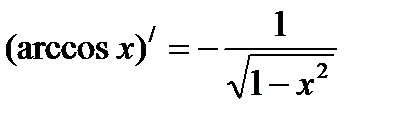
(ax)′ = ax ·ln a
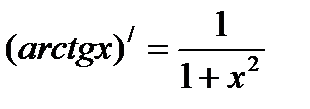
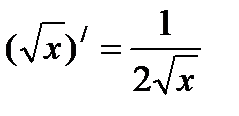
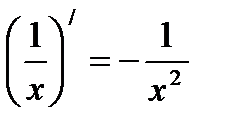
Пример1. Найти производную: 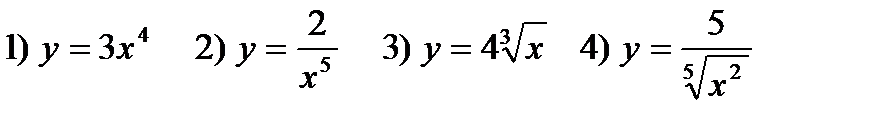
5) 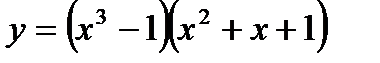 6)
6) 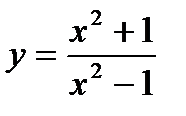
Решение.
1) 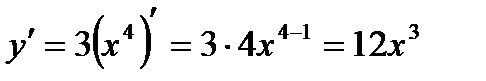 .
.
2) Перепишем функцию в виде, удобном для дифференцирования: 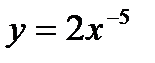 .
.
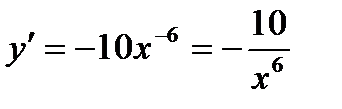 .
.
3) Перепишем функцию в виде, удобном для дифференцирования: 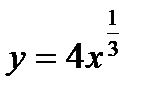 .
.
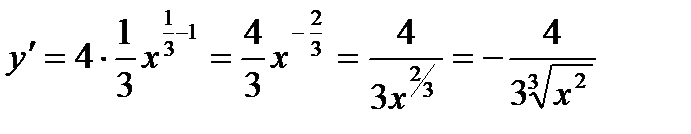 .
.
4) Перепишем функцию в виде, удобном для дифференцирования: 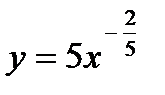 .
.
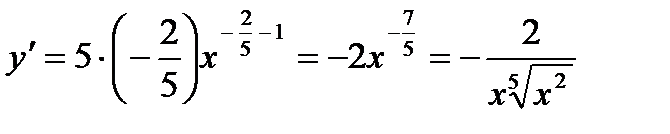 .
.
5) 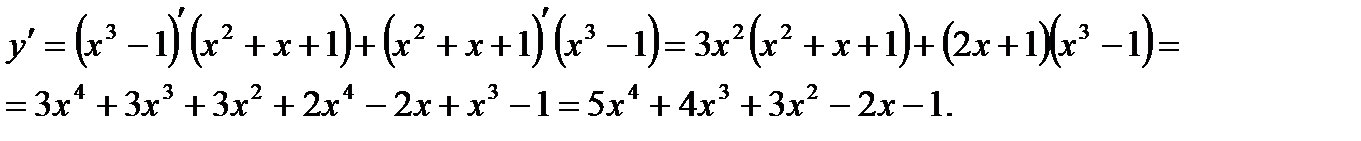
1.
6) 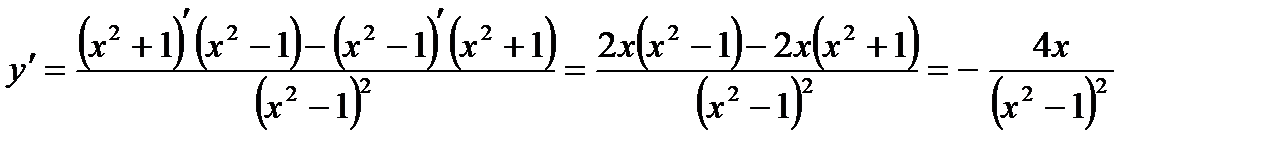 .
.
Пример2. Найти производную сложной функции: 1) 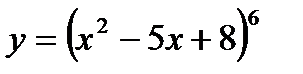
2) 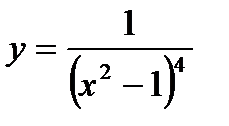 3)
3) 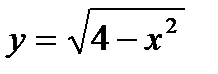 4)
4) 
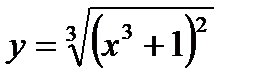 .
.
Решение. Производная сложной функции вычисляется по правилу дифференцирования 6.
1) 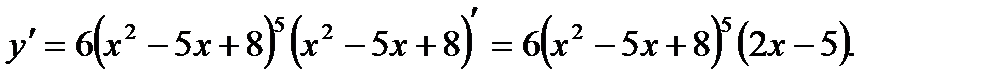
2) Перепишем функцию в виде, удобном для дифференцирования: 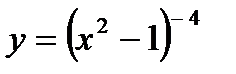 .
.
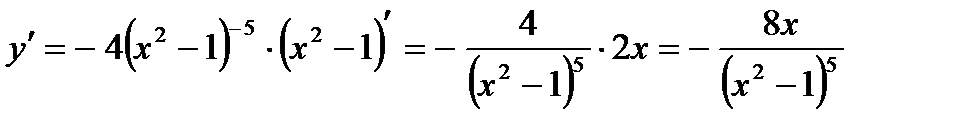
3) 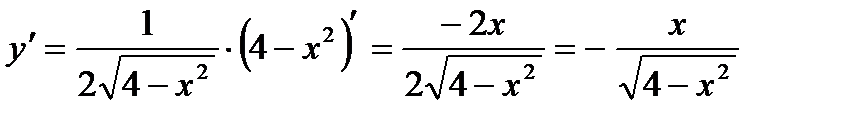 .
.
4) Перепишем функцию в виде, удобном для дифференцирования: 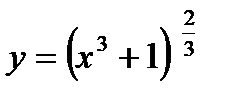 .
.
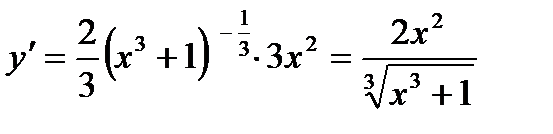 .
.
Определение. Функция F(x) называется первообразной для функции f(x) на промежутке, если в любой точке этого промежутка её производная равна f(x):
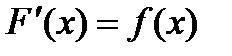 .
.
Отыскание первообразной функции есть действие, обратное дифференцированию, - интегрирование.
Определение. Совокупность первообразных для функции f(x) называется неопределённым интегралом и обозначается символом 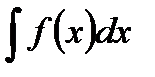 . Таким образом:
. Таким образом:
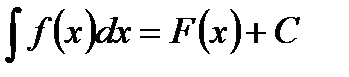 , где f(x)dx – подынтегральное выражение, С – постоянная.
, где f(x)dx – подынтегральное выражение, С – постоянная.
Свойства неопределённого интеграла.
1) Неопределённый интеграл суммы функций равен алгебраической сумме неопределённых интегралов этих функций.
2) Постоянный множитель подынтегрального выражения можно вынести за знак неопределённого интеграла.
3) Если функция имеет вид f(kx+b), то неопределённый интеграл вычисляется по формуле: 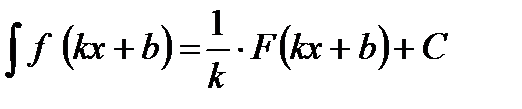 .
.
Таблица первообразных
| B - const | Bx + C |
| x n , n ≠ -1 | 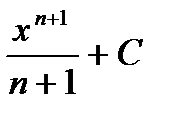 |
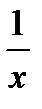 | Ln 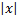 + C + C |
| e x | e x + C |
| sin x | - cos x + C |
| cos x | sin x + C |
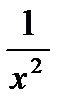 | 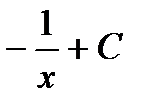 |
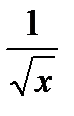 | 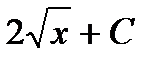 |
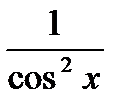 | tg x + C |
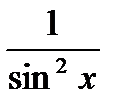 | - ctg x + C |
| ax , a>0 | 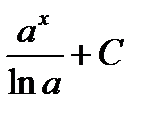 |
Определение. Приращение F(b) – F(a) любой из первообразных некоторой функции при изменении аргумента от х = а до х = b называется определённым интегралом от а до b функции f(x) и обозначается 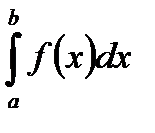 . Числа а и b называются пределами интегрирования.
. Числа а и b называются пределами интегрирования.
При вычислении определённого интеграла используется формула Ньютона-Лейбница: 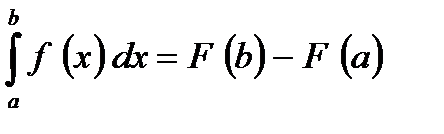 .
.
Пример 3. Найти: 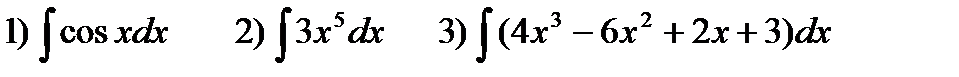 .
.
Решение. 1) 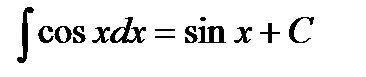 ;
;
2) 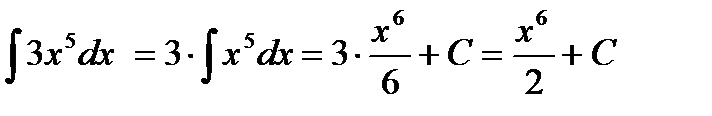 ;
;
3) 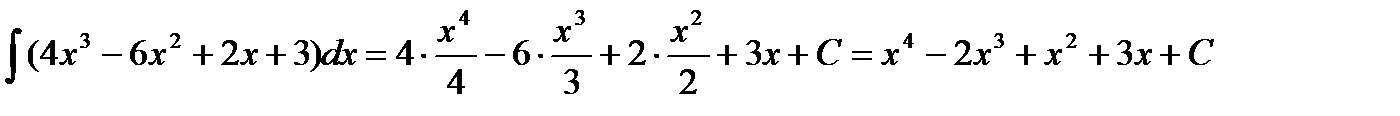 .
.
Пример 4. Вычислить: 1) 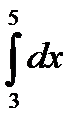 ; 2)
; 2) 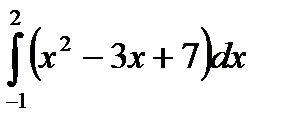 ; 3)
; 3) 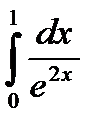 ; 4)
; 4) 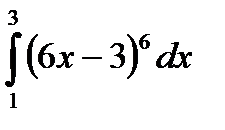 .
.
Решение. 1) 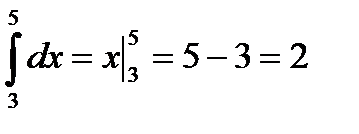 ;
;
2) 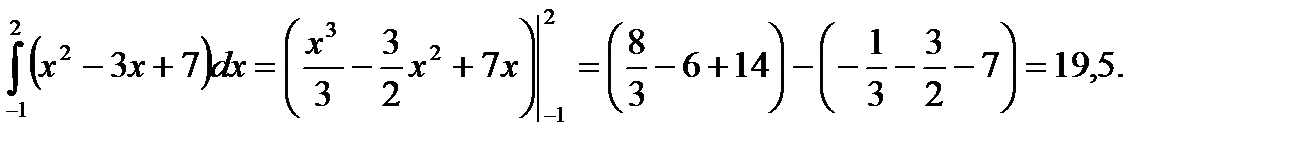
3) 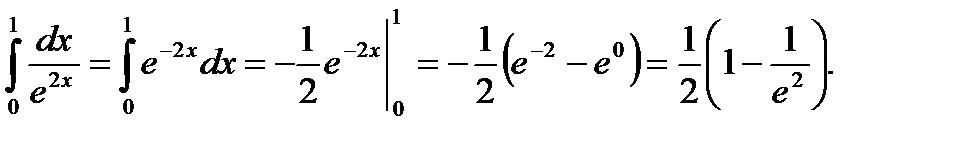
4) 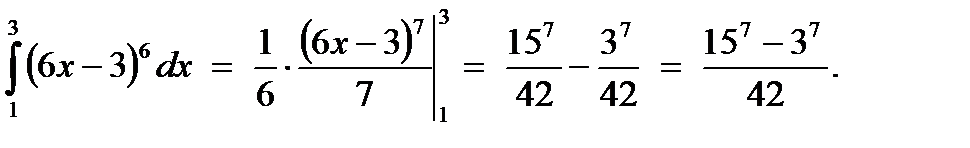
Определение. Числовым рядом называется сумма вида: 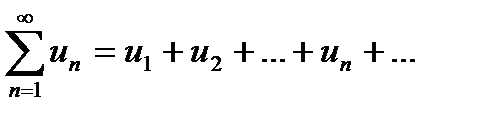 , где числа
, где числа 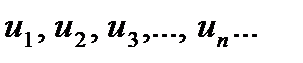 , называемые членами ряда, образуют бесконечную последовательность.
, называемые членами ряда, образуют бесконечную последовательность.
Каждому ряду можно сопоставить последовательность частичных сумм 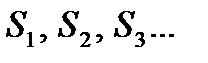 Если при бесконечном возрастании номера n сумма ряда Sn стремится к пределу S, то такой рад называется сходящимся, а число S – суммой сходящегося ряда.
Если при бесконечном возрастании номера n сумма ряда Sn стремится к пределу S, то такой рад называется сходящимся, а число S – суммой сходящегося ряда.
Если частичная сумма Sn при неограниченном возрастании п не имеет конечного предела, то такой ряд называется расходящимся.
Тригонометрическим рядом Фурье для функции f(x) в промежутке изменения аргумента -p £ х £ p называется ряд вида
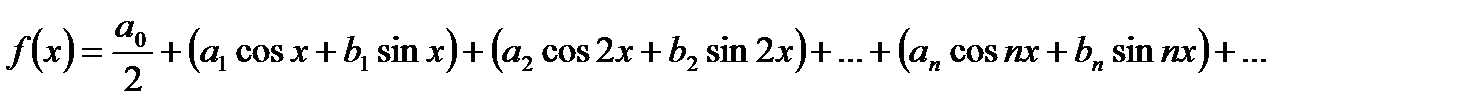
или короче: 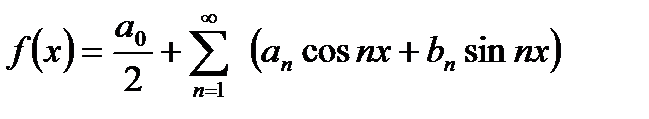 ,
,
где 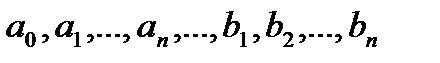 - коэффициенты ряда, называемые коэффициентами Фурье.
- коэффициенты ряда, называемые коэффициентами Фурье.
Разложение функции в тригонометрический ряд имеет важное значение в прикладных науках. Такое разложение называют гармоническим анализом.
Чтобы разложить периодическую функцию f(x) с периодом 2p в тригонометрический ряд, нужно найти коэффициенты этого ряда, которые вычисляются по формулам:
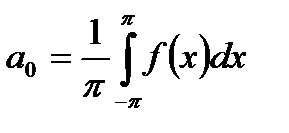 ,
,
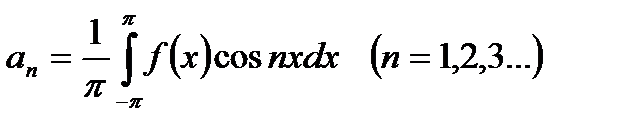 ,
, 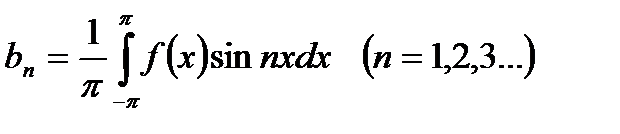 .
.
Упражнения для тренировки
Найти следующие интегралы:
1. 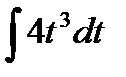
2. 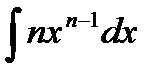
3. 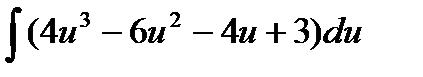
4. 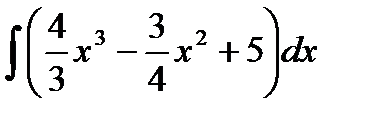
5. 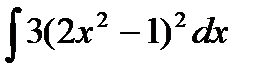
6. 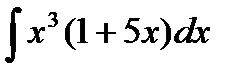
7. 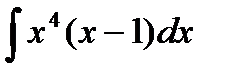
8. 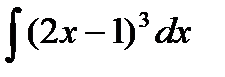
9. 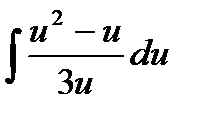
10. 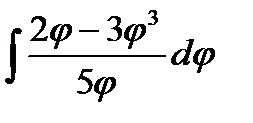
11. 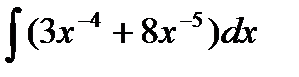
12. 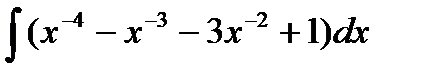
13. 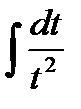
14. 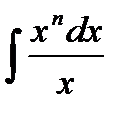
15. 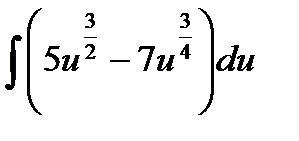
16. 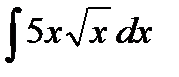
17. 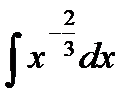
18. 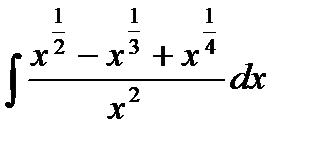
19. 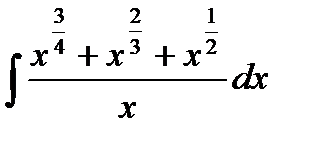
20. 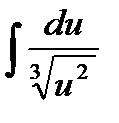
21. 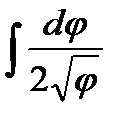
22. 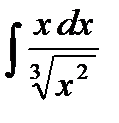
23. 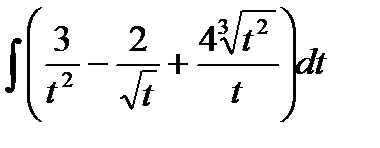
24. 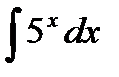
25. 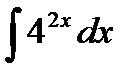
26. 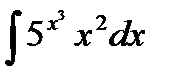
27. 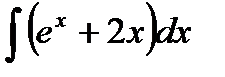
28. 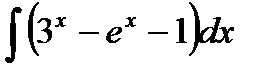
29. 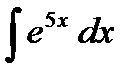
30. 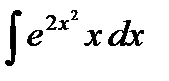
31. 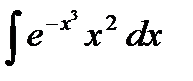
32. 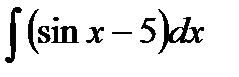
33. 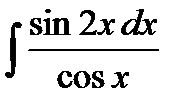
34. 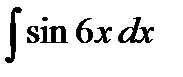
35. 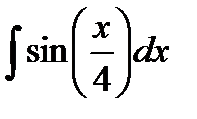
36. 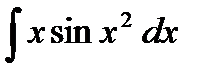
37. 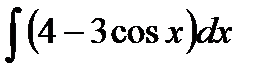
38. 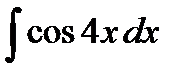
39. 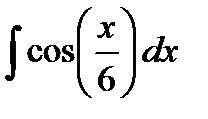
40. 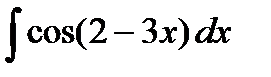
41. 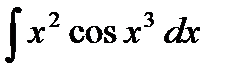
42. 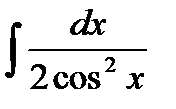
43. 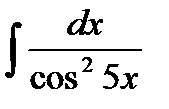
44. 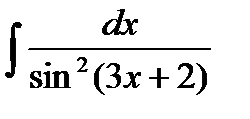
Вычислить определённые интегралы:
45. 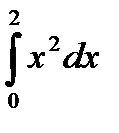
46. 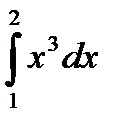
47. 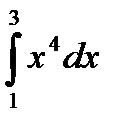
48. 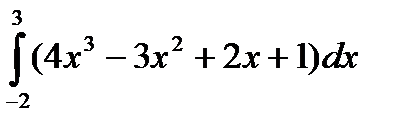
49. 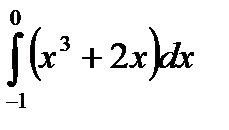
50. 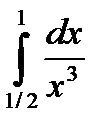
51. 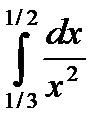
52. 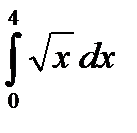
53. 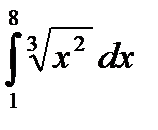
54. 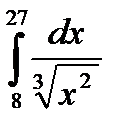
55. 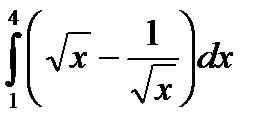
56. 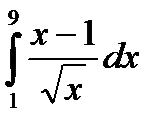
57. 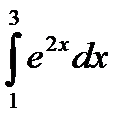
58. 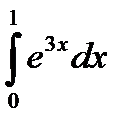
59. 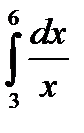
60. 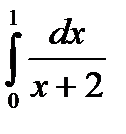
61. 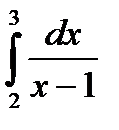
62. 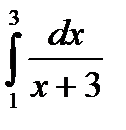
63. 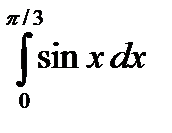
64. 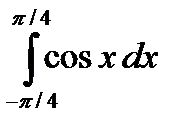
71. 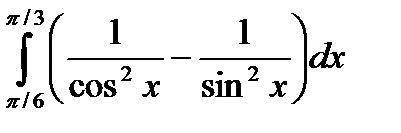
72. 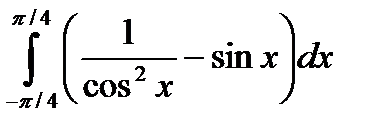
Разложить в ряд Фурье следующие периодические функции:
2.
73. 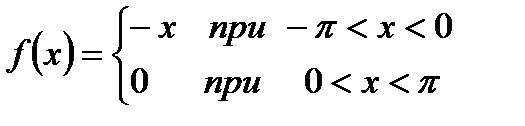 в промежутке -p £ х < p.
в промежутке -p £ х < p.
74. 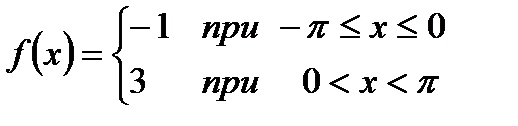 в промежутке -p < х < p.
в промежутке -p < х < p.
75. Разложить в ряд Фурье периодическую функцию 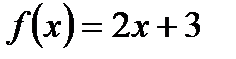 в промежутке -p < х < p.
в промежутке -p < х < p.
3.Для того, чтобы выполнить задание №4 домашней контрольной работы необходимо изучить теоретический материал раздела «Математический анализ», рассмотреть решенные задачи и попытаться решить упражнения для тренировки.
