Теоретические упражнения
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1) Линейное пространство. Базис. Координаты.
2) Преобразование координат вектора при переходе к новому базису.
3) Линейный оператор. Матрица оператора.
4) Преобразование матрицы оператора при переходе к новому базису.
5) Действия над линейными операторами.
6) Собственные векторы и собственные значения.
7) Евклидово пространство. Неравенство Коши—Буняковского.
8) Сопряженные и самосопряженные операторы. Их матрицы.
9) Ортогональное преобразование; свойства; матрица.
10) Квадратичные формы. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.
ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
1) Найти какой-нибудь базис и размерность подпространства 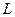 пространства
пространства 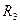 , если
, если 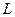 задано уравнением
задано уравнением 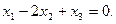
2) Доказать, что все симметрические матрицы третьего порядка образуют линейное подпространство всех квадратных матриц третьего порядка. Найти базис и размерность этого подпространства.
3) Найти координаты многочлена 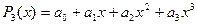 в базисе 1,
в базисе 1, 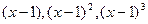 .
.
4) Линейный оператор 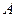 в базисе
в базисе 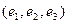 имеет матрицу
имеет матрицу
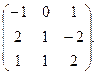
Найти матрицу этого же оператора в базисе 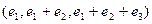 .
.
5) Найти ядро и образ оператора дифференцирования в пространстве многочленов, степени которых меньше или равны трем.
6) Пусть 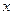 и
и 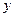 — собственные векторы линейного оператора
— собственные векторы линейного оператора 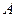 , относящиеся к различным собственным значениям. Доказать, что вектор
, относящиеся к различным собственным значениям. Доказать, что вектор 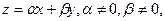 не является собственным вектором оператора
не является собственным вектором оператора 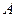 .
.
7) Пусть 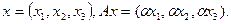 Будет ли оператор
Будет ли оператор 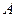 самосопряженным?
самосопряженным?
8) Доказать, что если матрица оператора А — симметрическая в некотором базисе, то она является симметрической в любом базисе (базисы — ортонормированные).
