Аграрлық-техникалық университеті», 2014
Мазмұны
| Кіріспе................................................................................................. | ||
| Есептеп-жобалау жұмыстарын орындаудың негізгі талаптары ... | ||
| 1.1 | Тапсырманың берілген мәндерін таңдап алу тәртібі..................... | |
| 1.2 | Титул бетті безендіру........................................................................ | |
| 1.3 | Есептеу түсініктемесін безендіру.................................................... | |
| 1.4 | Жұмыстың графикалық бөлімін орындау....................................... | |
| 1.5 | Есептеп-жобалау жұмыстарын қорғау............................................ | |
| Типтік есептерді шығару мысалдары | ||
| Бойлық деформацияға ұшыраған статикалық анықталмаған стержендер жүйесі............................................................................. | ||
| 2.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 2.2 | Мысал................................................................................................. | |
| Кернеулі және деформациялы күй.................................................. | ||
| 3.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 3.2 | Мысал................................................................................................. | |
| Жазық қималардың геометриялық сипаттамалары....................... | ||
| 4.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 4.2 | Мысал................................................................................................. | |
| Тік брустардың иілуі........................................................................ | ||
| 5.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 5.2 | Мысал................................................................................................. | |
| Қимасы дөңгелек стержендердің бұралуы...................................... | ||
| 6.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 6.2 | Мысал................................................................................................. | |
| Статикалық анықталмаған жазық жүйелерді есептеу................... | ||
| 7.1 | Есеп шығаруға арналған әдістемелік нұсқаулар............................ | |
| 7.2 | Мысал................................................................................................. | |
| Сығылған түзу стержендерді орнықтылыққа есептеу................... | ||
| 8.1 | Есепті шығаруға арналған әдістемелік нұсқау............................... | |
| 8.2 | Мысал................................................................................................. | |
| Пайдаланылған әдебиеттер тізімі.................................................... | ||
| Қосымша............................................................................................ |
КІРІСПЕ
«Материалдар кедергісі» курсын оқып танысқан кезде есептер шығару студенттердің инженерлік ойлау қабілеттерін белгілі бір сатыда дамытады және қажетті инженерлік конструкция элементерін беріктікке есептеуге дағдыландырады. Негізгі қиындықтар студенттердің өз бетімен есептеп-жобалау жұмыстарын орындағанда пайда болады. Сондықтан да практика жүзінде өзіндік есептеп-жобалау жұмыстарының орындалуына қажетті қосымша ңұсқаудың шығарылуы студенттердің үй тапсырмаларының орындалуын жетілдету мақсатын көздейді.
Әдістемелік нұсқауда үлгі ретінде курстың негізгі бөлімдері бойынша типтік есептердің шешімдері нақты қаралып, жеке есептен жобалау жұмыстарын орындауға арналған кафедраның негізгі талаптары келтірілген. Есептердің барлық шешімдері СИ системасында беріліп техникалық және технологиялық мамандықтардың студенттері үшін «Материалдар кедергісі» курсының бағдарламасына сәйкес құрастырылған.
1 ЕСЕПТЕП-ЖОБАЛАУ ЖҰМЫСТАРЫН ОРЫНДАУДЫҢ НЕГІЗГІ ТАЛАПТАРЫ
1.1 ТАПСЫРМАНЫҢ БЕРІЛГЕН МӘНДЕРІН ТАҢДАП АЛУ ТӘРТІБІ
Әрбір студенттің барлық есептеп-жобалау жұмыстары жеке болуы тиіс.
Жеке тапсырмалардың реттік нөмірлері жорналдағы студенттердің тізіміне байланысты. Студент есептің негізгі сан мәндерін вариантқа сәйкес кестеден таңдап алады.
Мысалы: Студент Асқаров Б тіркеу кітабындағы тізім бойынша 45-ші. Ол схема нөмірі 45, ал сан мәндері кестенің 41…60 жолына сәйкес келетін есепті шығаруы керек. Әрбір студент есептеу жұмысының түсініктемесін өрнектеуде әуелі есептеп-жобалау жұмысының атын, вариант нөмірін және берілген сан мәндерін жазады. Есептеу жұмысының барлық сан мәндерінің дәлдігі нөлден кейін екі санға дейін алынады. Мысалы: 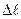 = 0,5674 мм = 0,57 мм.
= 0,5674 мм = 0,57 мм.
1.2 ТИТУЛ БЕТТІ БЕЗЕНДІРУ
Есептеп-жобалау жұмысы жөніндегі мәлеметтер өлшемі 210х297 мм жазба қағаздарында орындалады. Бірінші беті титул деп аталады, ГОСТ 2.105-68 бойынша өрнектеледі. Титул бетті толтыру үлгісі 1-ші суретте корсетілген.
Титул беттің барлық жазулары қатаң түрде қара сия және сызба шрифтісі арқылы жазылады.
«ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ»- шрифт -№7 немесе № 5;
«Жәңгір хан атындағы Батыс Қазақстан аграрлық-техникалық университеті» - шрифт № 5 немесе №3;
«К және ТО» кафедрасы - шрифт № 3,5;
«Материалдар кедергісі» пәнінен - шрифт №7;
«Есептеп-жобалау жұмыстары №1…..6» - шрифт №14;
«Орындаған», «Тексерген» - шрифт № 5;
Жұмысты орындаған жылы - шрифт № 5.

Сурет 1 – Титул бетін безендіру
1.3 ЕСЕПТЕУ ТҮСІНІКТЕМЕСІН БЕЗЕНДІРУ
Есептеу түсініктемесінің жазуы жеткілікті түрде қысқа болуы керек. Жазуда келтірілген формулалар біріншіден жалпы түрде алынып ықшамдау жұмысынан кейін оларға бастапқы сан мәндері бір өлшем жүйесінде қойылады.
Есептеу түсініктемесінің жазулары беттің бір жағында өте таза түрде бір түсті сиямен жазылады. Әр беттің сол жағынан 25 мм, үстінен, астынан 20 мм, ал оң жағынан 10 мм, қалдырады. Түсіктеме жазулары қысқартылмай бір түрде жазылуы керек, мысалы: «анықтаймыз», «есептейміз».
1.4 ЖҰМЫСТЫҢ ГРАФИКАЛЫҚ БӨЛІМІН ОРЫНДАУ
Жұмыстың графикалық бөлімі өлшемі 210x297 мм А4 форматы сызба қағазында карандашпен немесе сиямен орындалады.
Берілген есептің схемасы масштабпен сызылады. Оның астына ішкі күштер, деформациялар эпюралары тұрғызылады. Есептік схеманың ішкі күштері анықталған қималарын белгіленіп, есептелген ординаталардың мәндері көрсетіледі. Эпюрлер жіңішке сызықтармен конструкция элементерінің өсіне перпендикуляр бағытта штрихталады. Олардың ортасында оң «+» және теріс «-» таңбалары қойылады.
1.5 ЕСЕПТЕП-ЖОБАЛАУ ЖҰМЫСТАРЫН ҚОРҒАУ
Студент орындаған есептеу жұмысын семестрде бекітілген кезек бойынша оқытушыға тапсырады. Уақытында тапсырылған жұмыс ең алғашқы инженерлік пәнінің табысының кепілі болып табылады.
Қатесі түзетілген жұмыстар жеке түрде қорғалады. Егер оқытушыдан қосымша ескертулер болмаса, студент жұмысы тапсырылды деп есептеледі. Қорғалған жұмыстар оқытушыда қалдырылады.
Есептеп-жобалау жұмыстарын орындамаған немесе қорғамаған студент емтиханға жіберілмейді.
ТИПТІК ЕСЕПТЕРДІ ШЫҒАРУ МЫСАЛДАРЫ
2. Бойлық деформацияға ұшыраған статиқалық анықталмаған стержендер жүйесі
Тапсырма шарты. Абсолютті қатаң брустың бір ұшы жылжымайтын топсалы тірекке бекітілсе, ал екінші ұшы топса арқылы екі стерженге ілінген.
Есептің схемасын 2 суреттен, ал сандық мәндерін 1 кестеден алу керек.
Кесте 1 - №1 есептеп-жобалау жұмысының сандық мәндері
| Нұсқалар | 1- | 21-40 | 41-60 | 61-80 | 81-100 | 101-120 | 121-140 | 141-160 | 161-180 | |
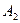 | см2 | |||||||||
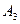 | см2 | |||||||||
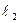 | м | 1,5 | 1,5 | 1,5 | ||||||
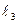 | м | 1,5 | 1,5 | 1,5 | 1,5 | |||||
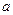 | м | 1,5 | 1,5 | 1,5 | ||||||
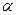 | град |
Талап етіледі:
1. Стержендердегі бойлық күштер мен кернеулерді жүк салмағымен Q өрнектеу;
2. Стержендердегі кернеулердің ең үлкен мәнін мүмкіндік кернеуіне теңестіріп (болат үшін [σ] = 160 МПа), жүк салмағының мүмкіндік мәнін [Qσ] анықтау;
3. Жүйенің ең үлкен жүк көтергіштігі арқылы Qкт жүк салмағының мүмкіндік мәнін [Qр] анықтау, егер болаттың аққыштық шегі σа.ш. = 240 МПа және беріктік қоры коэффициенті Кт = 1,5;
4. Екі әдіспен анықталған жүк салмағының мүмкіндік мәндерін салыстыра отырып, жүк салмағының қорытынды мүмкіндік мәнін қабылдау.
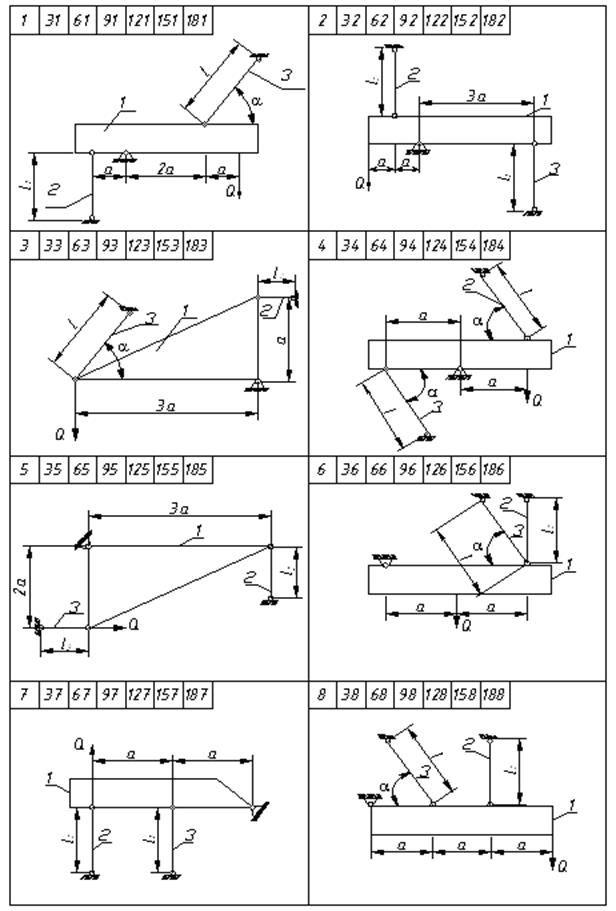
Сурет 2 – №1есептеп-жобалау жұмысының есептеу сұлбалары
2 суреттің жалғасы
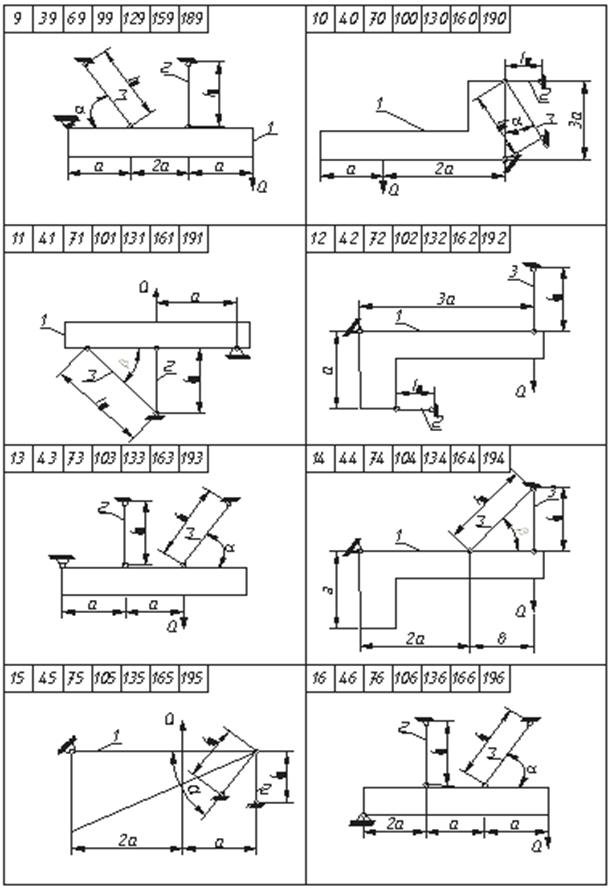
2 суреттің жалғасы
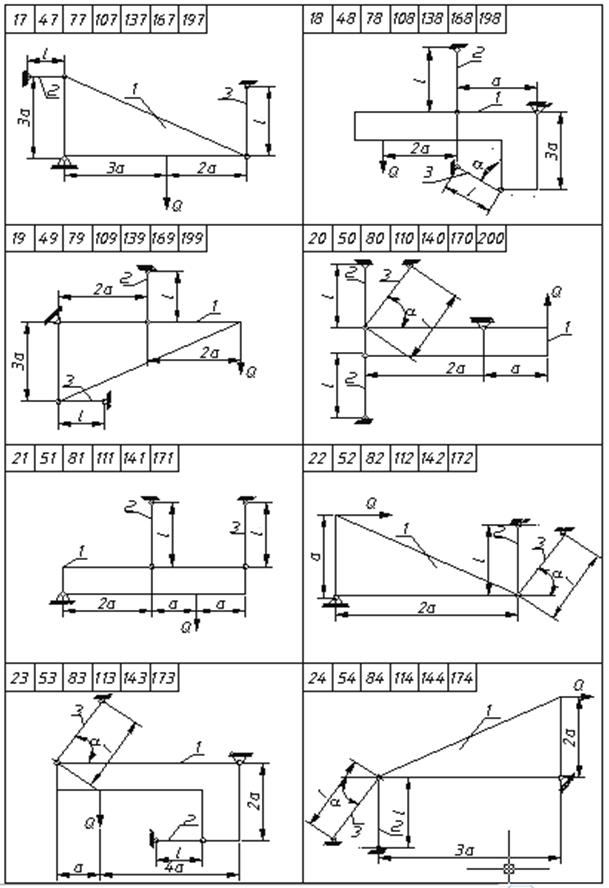
2 суреттің жалғасы
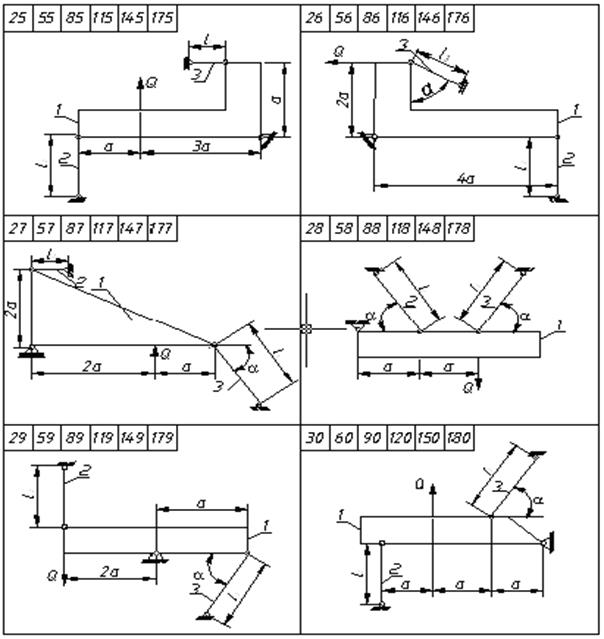
2.1 Есеп шығаруға арналған әдістемелік нұсқаулар
Стержендер бойынша пайда болатын ішкі күштер жазық жүйенің тепе-тендік теңдеулерінен анықталмаса онда бұл жүйелерге байланысты шығарылатын есептер статистиқалық анықталмаған деп аталады. Осы типтес есептерді шығару үшін төмендегі әдістемелік ңұсқауларды ескеру қажет:
а) есептің берілген шартымен танысып, қажетті жағдайда қосымша белгілер енгізу керек;
б) жүйені байланыстарын ажыратып тиісті реакцияларымен ауыстырылады;
в) статиканың мүмкін тепе-теңдік теңдеулері құрылып және олардын санын белгісіз ішкі күштермен салыстырып жүйенің статикалық анықталмау дәрежесі анықталады;
г) статикалық анықталмау дәрежесіне байланысты қосымша орын ауыстыру теңдеулері құрылады;
д) нүктелердің орын ауыстыруын Гук заңы бойынша өрнектеп стержендердің салыстырмалы деформациясының теңдеулері құрылады;
ж) деформация және тепе-теңдік теңдеулерді бірге шешіліп стержендегі бойлық күштер мен кернеулер Q күші арқылы өрнектеледі;
з) жүк салмағының мүмкіндік мәні [Q] екі әдіс бойынша есептеулердің нәтежелерін салыстыру арқылы анықталады (мүмкіндік кернеу және мүмкіндік күш әдістері).
ысал
Тапсырма шарты. Абсолютті қатаң брустың бір ұшы жылжымайтын топсалы тірекке бекітілсе, ал екінші ұшы топса арқылы екі стерженге ілінген (3, а - сурет).
Берілгені: 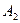 = 10 см2;
= 10 см2; 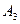 = 15 см2;
= 15 см2; 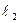 = 2 м;
= 2 м; 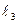 = 3 м;
= 3 м; 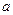 = 1,5 м;
= 1,5 м; 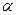 = 300; Стержендердің материалы - болат Ст 3.
= 300; Стержендердің материалы - болат Ст 3.
Талап етіледі:
1. Стержендердегі бойлық күштер мен кернеулерді жүк салмағымен Q өрнектеу;
2. Стержендердегі кернеулердің ең үлкен мәнін мүмкіндік кернеуіне теңестіріп (болат үшін [σ] = 160 МПа), жүк салмағының мүмкіндік мәнін [Qσ] анықтау;
3. Жүйенің ең үлкен жүк көтергіштігі арқылы Qкт жүк салмағының мүмкіндік мәнін [Qр] анықтау, егер болаттың аққыштық шегі σа.ш. = 240 МПа және беріктік қоры коэффициенті Кт = 1,5;
4. Екі әдіспен анықталған жүк салмағының мүмкіндік мәндерін салыстыра отырып, жүк салмағының қорытынды мүмкіндік мәнін қабылдау.
Шешуі:
Жүйені келесі ретпен белгілейміз: брус – 1; стержендер – 2 және 3.
Жазық жүйе үшін тепе-теңдік теңдеулерін құрамыз (3, а - сурет):
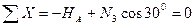 (2.1)
(2.1)
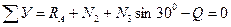 (2.2)
(2.2)
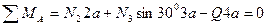 (2.3)
(2.3)
Созылу деформациясы кезіндегі беріктік шарты:
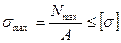 (2.4)
(2.4)
Жүйенің анықталмау дәрежесі:
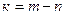 , (2.5)
, (2.5)
мұндағы m – белгісіз күштер саны, m = 5 (HА, RА, N2, N3, Q);
n – теңдеулер саны, n = 4.
Онда 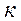 = 5 - 4 = 1, яғни жүйе бір рет статикалық анықталмаған.
= 5 - 4 = 1, яғни жүйе бір рет статикалық анықталмаған.
Есептің шарты бойынша ХА және УА анықтау керек емес, сондықтан есептеу жұмысында тепе-теңдік теңдеулерінің тек қана (2.3) теңдеуін қолданамыз.
Жүк салмағының мүмкіндік мәнін анықтау үшін екі әдісті қолданамыз: мүмкіндік кернеу және мүмкіндік күш.
1 әдіс
Жазық жүйенің деформациясын қарастырып, абсолютті қатаң брусты «А» топсасына байланысты шексіз кіші бұрышқа бұрамыз. Брустың бойындағы В және С нүктелері вертикаль бағытта төмен қарай δВ және δС шамаларына орын ауыстырып В' және С' сәйкес келеді (3, б - сурет). Тік бұрышты үшбұрыштардың ұқсастығынан (АВВ' және АСС') В және С нүктелерінің орын ауыстыру шамалары бір-бірімен байланысы төмендегі теңдеумен өрнектеледі:
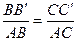
немесе
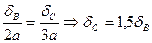 (2.6)
(2.6)
Деформациялардың шексіз кішілігін ескере отырып В және С нүктелерінің вертикаль орын ауыстыру шамаларын 2 және 3 стержендердің абсолтюттік бойлық деформацияларымен өрнектейміз:
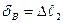 ,
, 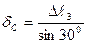 . (2.7)
. (2.7)
(2.6) және (2.7) теңдеулерді бірге шеше отырып, аламыз:
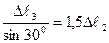 . (2.8)
. (2.8)
Гук заңы бойынша:
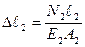 ,
, 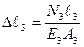 . (2.9)
. (2.9)
Онда (2.9) теңдеуін ескеріп, (2.8) теңдеуді келесі түрге келтіреміз:
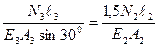 . (2.10)
. (2.10)
Бұл теңдеуге сандық мәндерді қоя отырып, аламыз (Е2 = Е3 = Е):
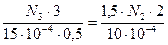 немесе
немесе 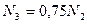 . (2.11)
. (2.11)
(2.3) және (2.11) теңдеулерінің көмегімен стержендердегі N2 және N3 бойлық күштерді Q арқылы өрнектейміз:
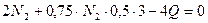 ,
,
Осыдан 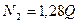 , онда
, онда 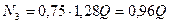 (2.12)
(2.12)
Стержендердегі кернеу:
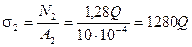 ,
, 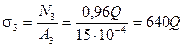 . (2.13)
. (2.13)
Стержендердегі ең үлкен кернеуді ( 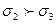 ) мүмкіндік кернеуіне [σ] теңеп жүк салмағының мүмкіндік мәнін [Qσ] анықтаймыз:
) мүмкіндік кернеуіне [σ] теңеп жүк салмағының мүмкіндік мәнін [Qσ] анықтаймыз:
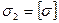 немесе 1280Q = [σ] (2.14)
немесе 1280Q = [σ] (2.14)
Осыдан 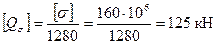 .
.
2 әдіс
Жүк салмағын арттырғанда «2» стержендегі кернеудің мәні «3» стержендегі кернеуге қарағанда аққыштық шекке ерте жетеді. Бірақ, бұл стержендегі кернеудің мәні аққыштық шекке жеткеннен кейін көпке дейін өспейді.
Бойлық күш мәні:
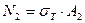 . (2.15)
. (2.15)
Жүк салмағының одан әрі өсуі «3» стержендегі кернеудің мәнінің аққыштық шекке жетуіне әкеліп соқтырады.
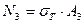 . (2.16)
. (2.16)
Жүк салмағының ең үлкен мәні (Q = Qкт) жүйенің ең үлкен жүк көтергіштігі деп аталады.
(2.15) және (2.16) теңдеулерді (2.3) теңдеуге қойып, жүйенің ең үлкен жүк көтергіштігін анықтаймыз:
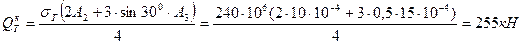 . (2.17)
. (2.17)
Беріктік қоры коэффициенті Кт = 1,5 болғанда, жүк салмағының мүмкіндік мәні [Qр]:
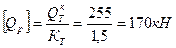 . (2.18)
. (2.18)
Жүк салмағының қорытынды мүмкіндік мәнін анықтау үшін екі әдіс нәтижелерін салыстырамыз:
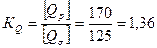 . (2.19)
. (2.19)
Қорытынды:
1). Егер 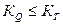 болса, онда пластикалық материалдан жасаған статикалық анықталмаған жүйені екінші әдіспен есептеу қажет. Себебі, бірінші әдіске қарағанда материал аз жұмсалады және жүйеде қалдық деформация болмауына толық кепілдік бар.
болса, онда пластикалық материалдан жасаған статикалық анықталмаған жүйені екінші әдіспен есептеу қажет. Себебі, бірінші әдіске қарағанда материал аз жұмсалады және жүйеде қалдық деформация болмауына толық кепілдік бар.
2). Егер 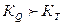 болса, онда берілген жүйені екінші әдіспен есептеуге болмайды. Себебі, жүйеде қалдық деформация пайда болады.
болса, онда берілген жүйені екінші әдіспен есептеуге болмайды. Себебі, жүйеде қалдық деформация пайда болады.
Берілген есеп үшін 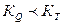 , яғни 1,36 < 1,5
, яғни 1,36 < 1,5
Онда [Q] = 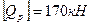 .
.
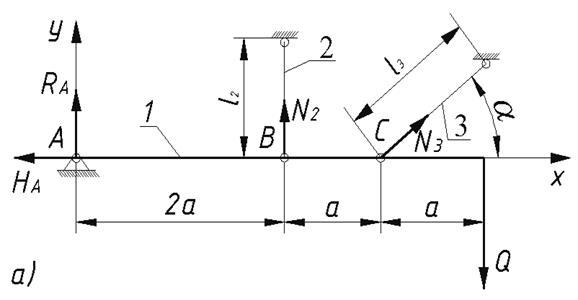
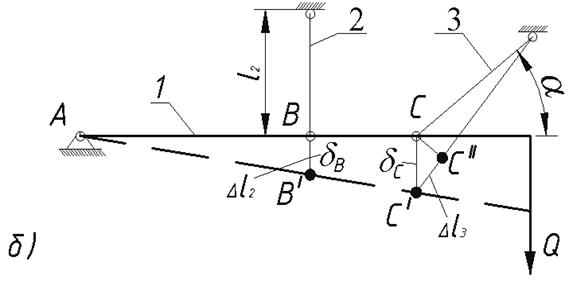
Сурет 3 – №1 есептеп-жобалау жұмысының есептеу сұлбасы
3.Кернеулі және деформациялы күй
Тапсырма шарты. Болаттан жасалған куб күш әсерінен жазықтық кернеулі күйде.
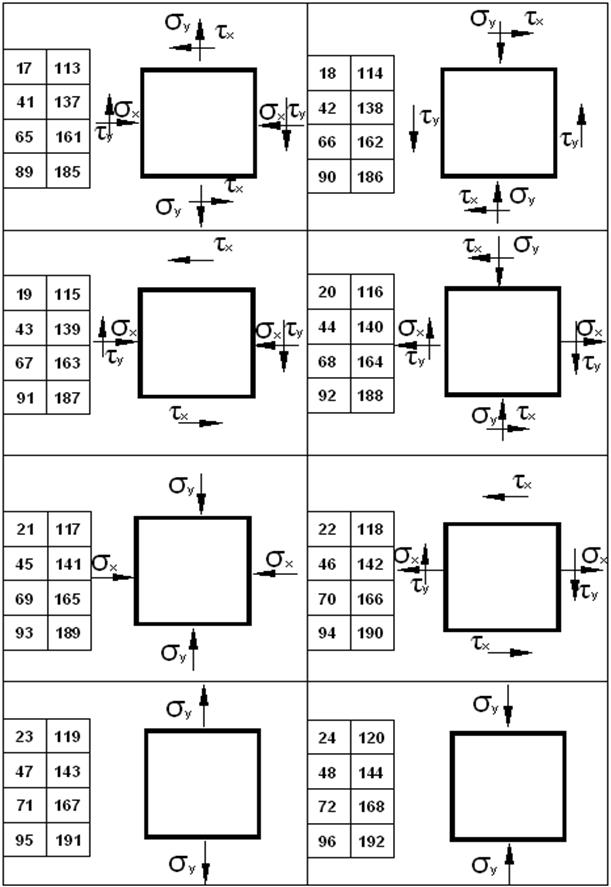
Нүктенің жазық кернеулі күйіне талдау жүргізу. Кернеулі күйдің сұлбасын 4 суреттен, ал сандық мәндерін 2 кестеден аламыз.
Ескерту: Есептеген кезде 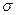 және
және 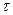 кернеулерінің таңбалары сұлбадағы бағыттарына сәйкес қабылданады.
кернеулерінің таңбалары сұлбадағы бағыттарына сәйкес қабылданады.
Кесте 2 - №2 есептеп-жобалау жұмысының сандық мәндері
| Нұсқалар | 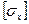 | 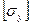 | 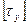 |
| МПа | МПа | МПа | |
| 1-20 | |||
| 21-40 | |||
| 41-60 | |||
| 61-80 | |||
| 81-100 | |||
| 101-120 | |||
| 121-140 | |||
| 141-160 | |||
| 161-180 |
Талап етіледі:
1. Басты кернеулерді және басты аудандардың орындарын анықтау.
2. Ең үлкен және ең кіші жанама кернеулерді және оған сәйкес келетін ауданды анықтау.
3. Салыстырмалы деформацияны есептеу.
4. Көлемнің салыстырмалы өзгеруін есептеу.
5. Деформацияның меншікті потенциялдық энергиясын есептеу.
6. Кернеулі күйдің сұлбасын барлық сандық мәндерімен салу.
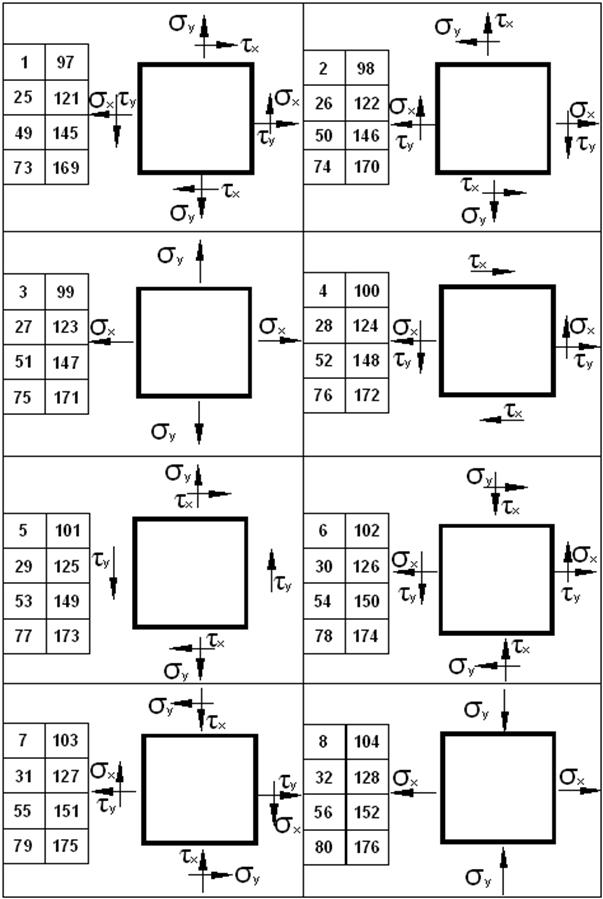 Сурет 4 - №2 есептеп-жобалау жұмысының есептеу сұлбалары
Сурет 4 - №2 есептеп-жобалау жұмысының есептеу сұлбалары
4 суреттің жалғасы
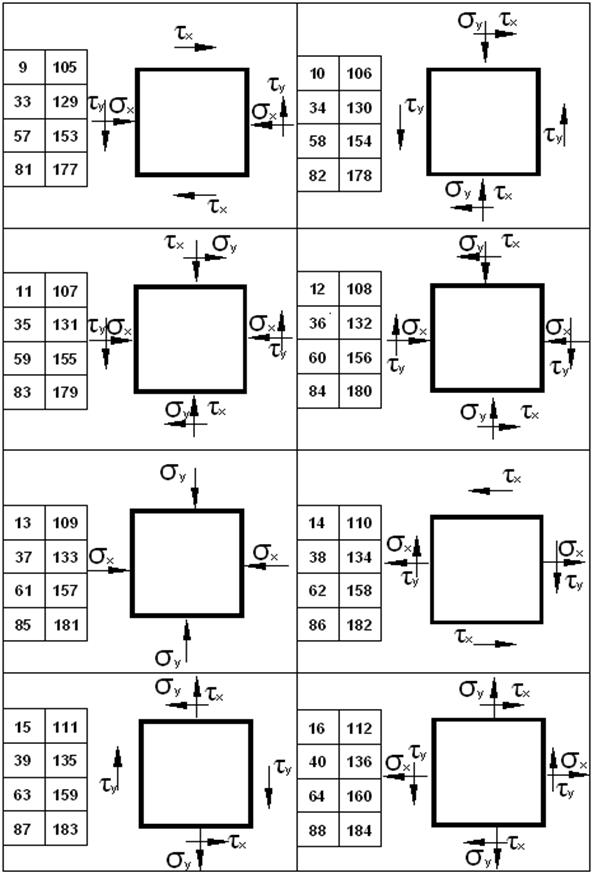
4 суреттің жалғасы
3.1 Есеп шығаруға арналған әдістемелік нұсқаулар
а) Берілген схемаға байланысты 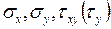 кернеулерінің таңбалары қойылады: созушы тік кернеу оң «+», ал сығушы – теріс «-». Жанама кернеу векторы дененің кез келген нүктесіне байланысты сағат тілі бойынша бағытталса оң «+», ал сағат тіліне қарсы – теріс «-». Берілген тік қабырғаны көлбеу жазықтықпен беттестіру үшін сағат тіліне қарсы бұрылса αбұрышы оң «+», ал сағат тілі бойынша – теріс «-».
кернеулерінің таңбалары қойылады: созушы тік кернеу оң «+», ал сығушы – теріс «-». Жанама кернеу векторы дененің кез келген нүктесіне байланысты сағат тілі бойынша бағытталса оң «+», ал сағат тіліне қарсы – теріс «-». Берілген тік қабырғаны көлбеу жазықтықпен беттестіру үшін сағат тіліне қарсы бұрылса αбұрышы оң «+», ал сағат тілі бойынша – теріс «-».
б) Тік кернеудің экстремалды мәндерді 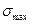 ,
, 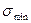 есептеліп басты кернеулер (
есептеліп басты кернеулер ( 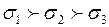 ) анықталады;
) анықталады;
в) басты аудандардың орындары 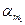 және
және 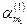 , анықталып,
, анықталып, 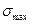 ,
, 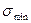 ,
, 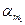 ,
, 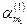 мәндері тексеріледі;
мәндері тексеріледі;
г) жанама кернеудің ең үлкен және кіші мәндері 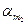 ,
, 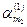 , есептеліп, ығысу ауданшаларының орындары анықталады;
, есептеліп, ығысу ауданшаларының орындары анықталады;
д) Гуктың жалпылама заңы бойынша сызықтық салыстырмалы деформациялар 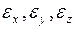 есептеледі;
есептеледі;
е) көлемнің салыстырмалы өзгеруі анықталады;
ж) деформацияның меншікті потенциялдық энергиясы есептеледі.
ысал
Тапсырма шарты. Болаттан жасалған куб күш әсерінен жазықтық кернеулі күйде (5 сурет).
Берілгені: 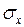 =200 H/м2 ;
=200 H/м2 ; 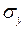 = -100 H/м2 ;
= -100 H/м2 ; 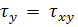 = -200 H/м2;
= -200 H/м2;
E=2 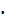 105MПа; µ=0,3
105MПа; µ=0,3
Талап етіледі:
1. Басты кернеулерді және басты аудандардың орындарын анықтау.
2. Ең үлкен және ең кіші жанама кернеулерді және оған сәйкес келетін ауданды анықтау.
3. Салыстырмалы деформацияны есептеу.
4. Көлемнің салыстырмалы өзгеруін есептеу.
5. Деформацияның меншікті потенциялдық энергиясын есептеу.
6. Кернеулі күйдің сұлбасын барлық сандық мәндерімен салу.
Шешуі:
Тік кернеудің экстрамальді мәндері 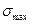 және
және 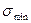
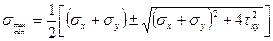 (3.1)
(3.1)
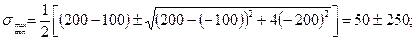
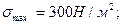
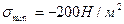
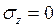 және
және 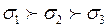 ескере отырып, басты кернеулерді анықтаймыз.
ескере отырып, басты кернеулерді анықтаймыз.
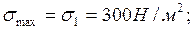
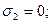
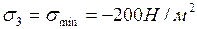
Басты аудандардың орындары
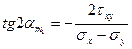 (3.2)
(3.2)
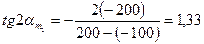
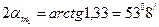
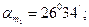
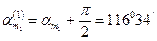
ТЕКСЕРУ:
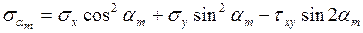 (3.3)
(3.3)
(3.3)формулаға сүйір бұрыштың мәні қою ұсынылады.
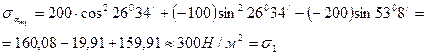
Қорытынды: 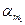 және
және 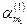 бұрыштары дұрыс анықталған, себебі
бұрыштары дұрыс анықталған, себебі 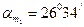 әсер ететін басты ауданға сәйкес келеді. Бұрышы оң болғандықтан оны берілген вертикаль ауданшадан сағат тіліне қарсы бағытта саламыз (cурет 6)
әсер ететін басты ауданға сәйкес келеді. Бұрышы оң болғандықтан оны берілген вертикаль ауданшадан сағат тіліне қарсы бағытта саламыз (cурет 6)
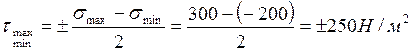 (3.4)
(3.4)
Ең үлкен жанама кернеуге 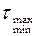 ,сәйкес келетін аудан басты ауданға 45° орналасқан.
,сәйкес келетін аудан басты ауданға 45° орналасқан.
Демек:
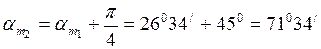 (3.5)
(3.5)
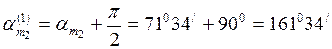
ТЕКСЕРУ:
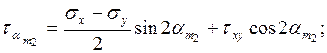 (3.6)
(3.6)
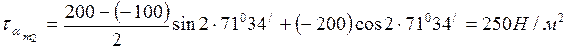
ҚОРЫТЫНДЫ: 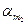 бұрышының мәні дұрыс анықталған және ол
бұрышының мәні дұрыс анықталған және ол 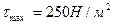 әсер ететін ауданға сәйкес келеді.
әсер ететін ауданға сәйкес келеді.
Салыстырмалы деформациялар төмендегі Гуктың қалпылама заңы бойынша анықталады.
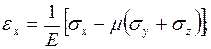
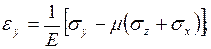 (3.7)
(3.7)
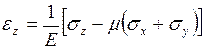
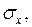
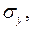
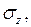
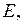
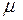 мәндерін орындарына қойсақ
мәндерін орындарына қойсақ
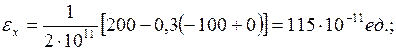
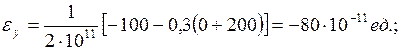
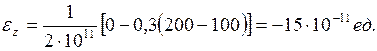
Дененің көлемінің салыстырмалы өзгеруі
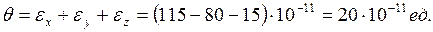 (3.8)
(3.8)
ТЕКСЕРУ:
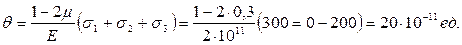 (3.9)
(3.9)
Деформацияның меншікті потенциялдық энергиясы
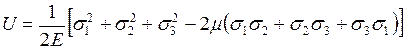 (3.10)
(3.10)
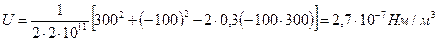
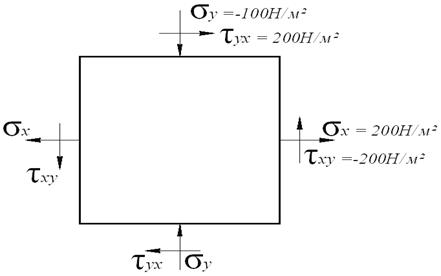
Сурет 5 – Берілген кернеулі күй
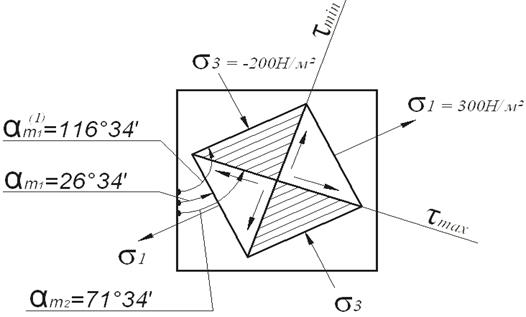
Сурет 6 – Басты аудан мен ығысу аудан орындарының
графикалық көрсетілу
4. Жазық қималардың геометриялық сипаттамалары
Тапсырма шарты. Күрделі қима швеллерден, қоставрдан, тік төртбұрышты қимадан және тең бүйірлі бұрыштамадан құралған (7 сурет).
Кесте 3 - №3 есептеп-жобалау жұмысының сандық мәндері
| Нұсқалар | Тік төртбұрыш | Қоставр | Швеллер | Бұрыштама | |
| h | δ | 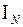 | [ N | в×в×d | |
| мм | мм | ||||
| 1-20 | 125х125х16 | ||||
| 21-40 | 160х160х18 | ||||
| 41-60 | 220х220х16 | ||||
| 61-80 | 100х100х10 | ||||
| 81-100 | 180х180х20 | ||||
| 101-120 | 200х200х20 | ||||
| 121-140 | 160х160х20 | ||||
| 141-160 | 125х125х16 | ||||
| 161-180 | 140х140х10 |
Талап етіледі:
1. Қиманың ауырлық центрінің орнын анықтау;
2. Қиманың ауырлық центрі арқылы өтетін 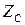 және
және 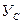 өстеріне байланысты өстік және центрден тепкіш инерция моментерін анықтау;
өстеріне байланысты өстік және центрден тепкіш инерция моментерін анықтау;
3. Басты орталық инерция өстерінің орындарын анықтау;
4. Қиманың ең үлкен және кіші өстік инерция моменттерін анықтау;
5. Қиманы 1:2 маштабымен сызып, сызба барлық өлшемдерді және өстерді көрсету.
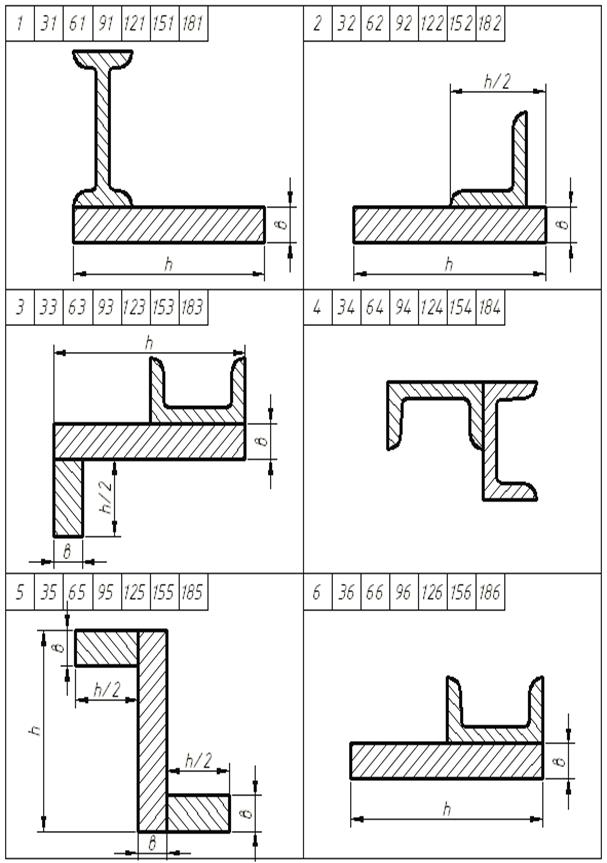
Сурет 7 - №3 есептеп-жобалау жұмысының есептеу сұлбалары
7 суреттің жалғасы
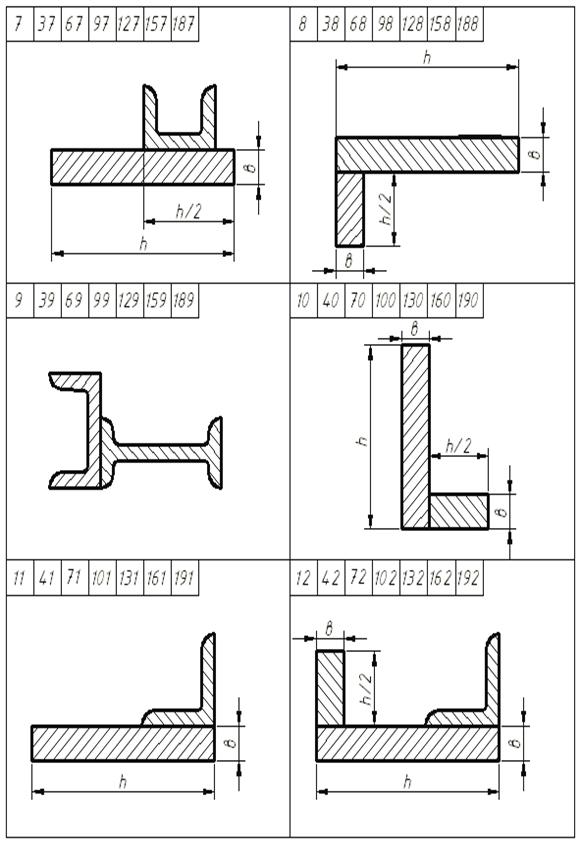
7 суреттің жалғасы
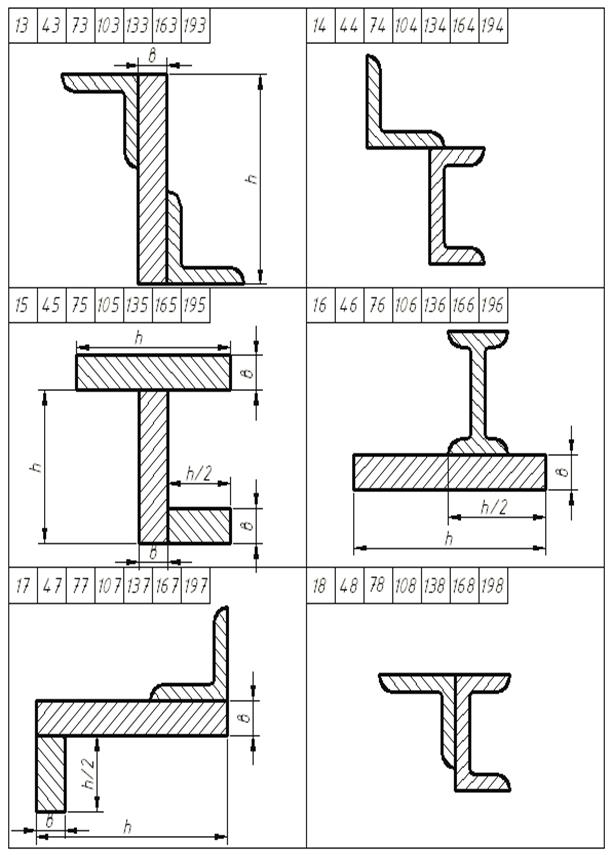
7 суреттің жалғасы
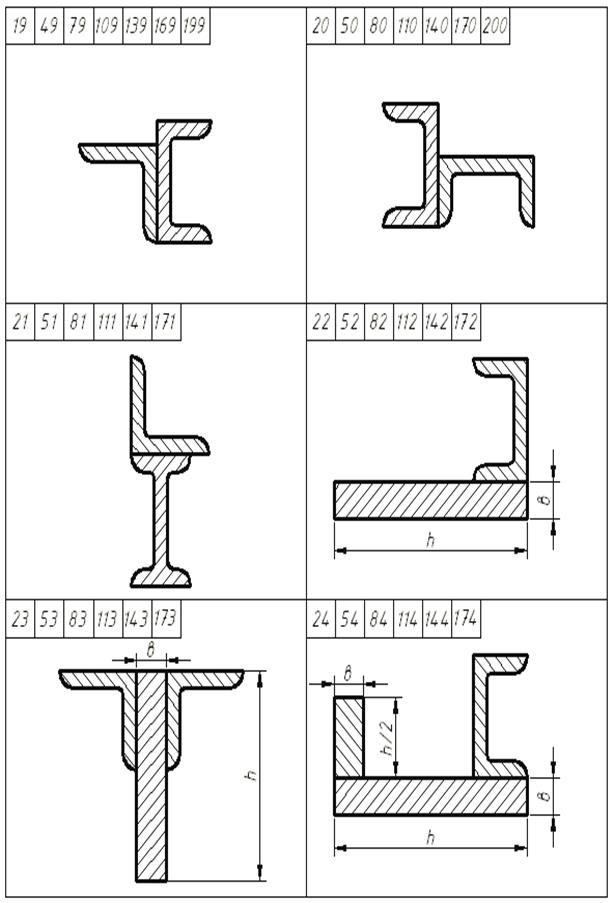
7 суреттің жалғасы
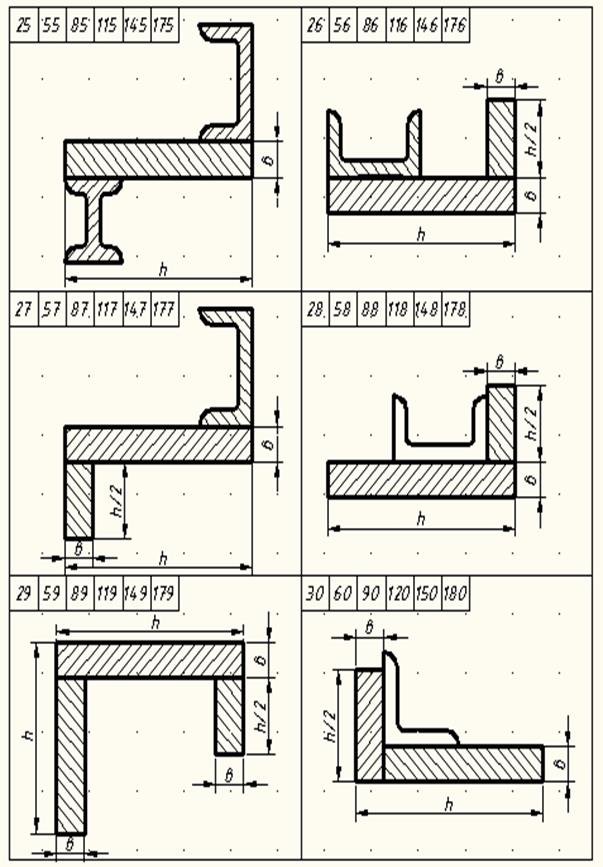
4.1 Есеп шығаруға арналған әдістемелік нұсқаулар
а) Мемлекеттік стандарт кестелерінен сызбадағы прокат профильдеріне қажетті және геометриялық сиппатамаларды жазып алу керек;
б) Қиманы 1:2 маштабымен А4 форматына сызып, оның қажетті өлшемдері көрсетіледі;
в) Күрделі қима қарапайым дара фигураларға бөлініп, оның кез келген нүктесі арқылы көмекші немесе «кездейсоқ» координат өстері Zo, Yo жүргізіледі;
г) Zo , Yo, өстеріне байланысты әр фигураның ауырлық центрінің орындары (С1, С2, Сi) анықталып, олар арқылы көмекші өстерге Zo , Yo паралелль жеке өстері Zi , Yi жургізіледі;
д) Күрделі қиманың ауырлық центрінің координаталары Zс және Yс қосымша өстерге Zo және Yo байланысты анықталып, графикалық жолмен тексеріледі;
е) Сызбада күрделі қиманың ауырлық центрі арқылы қосымша өстерге Zо және Yо паралелль орталық Zс және Yс өстері жүргізіледі;
ж) Әр фигураның ауырлық центрінің координаталары ai , bi Zс және Yc өстеріне өстеріне байланысты анықталып, сызбада көрсетіледі;
з) Күрделі қиманың Zc және Yc өстеріне байланысты өстік инерция 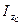 ,
, 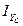 және центрден тепкіш инерция
және центрден тепкіш инерция 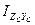 моменттері анықталады;
моменттері анықталады;
ЕСКЕРТУ! Өстік инерция моментерінің мәні әр уақытта оң танбалы «+», ал центрден тепкіш инерция моментінің мәні - теріс «-» немесе оң «+» болуы мүмкін.
и) Қиманың басты орталық инерция өстерінің U, V орындары α1 , α2 анықталады. Егер α > 0 болса, онда бұрыштың мәні Zc және Yc өстеріне сағат тіліне қарсы бағытта, ал α < 0 – сағат тілі бағытында салынады;
к) Өстік инерция моменті үлкен басты орталық инерция өсі Zc немесе Yc өстерімен кіші бұрыш жасайды. Мысалы: егер 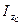 >
> 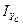 ,болса, онда U өсі мен Zc өсінің арасындағы бұрыш – кіші сүйір бұрыш, ал U- ең үлкен басты орталық инерция өсі;
,болса, онда U өсі мен Zc өсінің арасындағы бұрыш – кіші сүйір бұрыш, ал U- ең үлкен басты орталық инерция өсі;
л) Инерция моментерінің ең үлкен мәндері 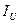 ,
, 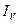 есептеледі;
есептеледі;
м) U және V өстеріне байланысты басты инерция моменттерінің 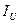 ,
, 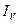 мәндерінің анықталуы тексеріледі. Дұрыстық шарты
мәндерінің анықталуы тексеріледі. Дұрыстық шарты 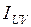 =0.
=0.
ысал
Тапсырма шарты. Күрделі қима швеллерден, тік төртбұрышты қимадан және тең бүйірлі бұрыштамадан құралған (8 сурет).
Талап етіледі:
1. Қиманың ауырлық центрінің орнын анықтау;
2. Қиманың ауырлық центрі арқылы өтетін 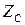 және
және 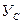 өстеріне байланысты өстік және центрден тепкіш инерция моментерін анықтау;
өстеріне байланысты өстік және центрден тепкіш инерция моментерін анықтау;
3. Басты орталық инерция өстерінің орындарын анықтау;
4. Қиманың ең үлкен және кіші өстік инерция моменттерін анықтау;
5. Қиманы 1:2 маштабымен сызып, сызба барлық өлшемдерді және өстерді көрсету.
Шешуі:
Сортамент кестесінен есептеуге қажетті мәндерді жазып аламыз:
№16 швеллер үшін:
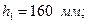
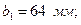
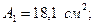
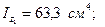
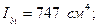
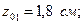
Тік төртбұрышты қима үшін:
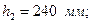
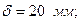
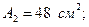
Тең бүйірлі бұрыштама 80×80×6 үшін:
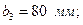
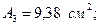
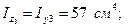
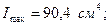
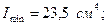
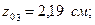
Күрделі қиманы 1:2 маштабымен сызамыз (8 сурет).
Қиманың ауырлық центрін анықтау үшін 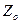 және Yо қосымша өстерін жүргізіп, оның координаталарын төмендегі формуламен есептейміз
және Yо қосымша өстерін жүргізіп, оның координаталарын төмендегі формуламен есептейміз
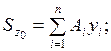 (4.1)
(4.1)
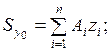 (4.2)
(4.2)
мұндағы 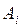 - і-ші фигураның ауданы;
- і-ші фигураның ауданы;
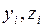 - і-ші фигураның ауырлық центрінің координаталары.
- і-ші фигураның ауырлық центрінің координаталары.
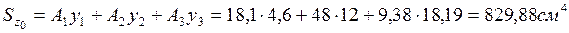
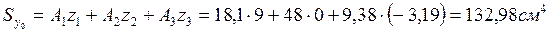
Осыдан
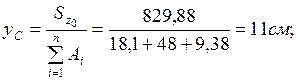
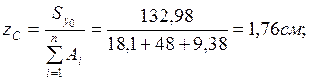
Сызбада 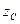 және
және 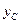 көрсетіп, С нүктесінің дұрыс анықталғандығын графикалық жолмен фигуралардың аудандарының ара қатынасы арқылы тексереміз (8 сурет).
көрсетіп, С нүктесінің дұрыс анықталғандығын графикалық жолмен фигуралардың аудандарының ара қатынасы арқылы тексереміз (8 сурет).
Күрделі қиманы Zс және Yс орталық өстеріне байланысты өстік және центрден тепкіштік инерция моменттері өстердің паралелль орын ауыстыру формуларымен анықталады
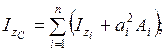 (4.3)
(4.3)
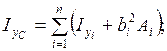 (4.4)
(4.4)
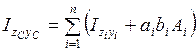 (4.5)
(4.5)
мұндағы 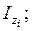
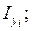
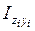 - і-ші фигураның Zс және Yс өстеріне параллель жеке орталық өстеріне Zi , Yi байланысты өстік және центрден тепкіштік инерция моменттері;
- і-ші фигураның Zс және Yс өстеріне параллель жеке орталық өстеріне Zi , Yi байланысты өстік және центрден тепкіштік инерция моменттері;
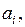
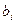 -
- 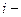 ші фигураның жеке Zi , Yi орталық өстерінен Zс және Yс өстеріне дейінгі арақашықтықтар.
ші фигураның жеке Zi , Yi орталық өстерінен Zс және Yс өстеріне дейінгі арақашықтықтар.
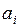 ,
, 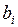 шамалары төмендегі формулалалармен есептеледі
шамалары төмендегі формулалалармен есептеледі
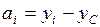 (4.6)
(4.6)
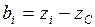 (4.7)
(4.7)
Олардың мәндері:
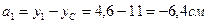
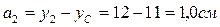
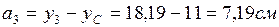
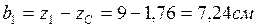
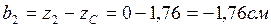
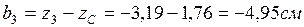
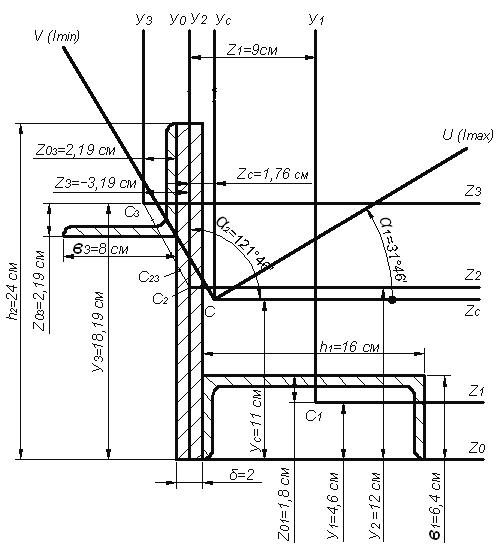
Сурет 8 – Күрделі қиманың геометриялық сипаттамаларын анықтау үшін есептеу сұлбасы
Онда өстік инерция моменттері
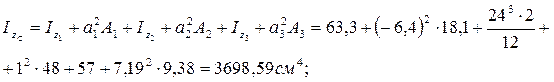
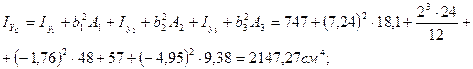
мұндағы 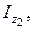
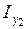 - тік төртбұрышты қиманың жеке орталық инерция өстеріне
- тік төртбұрышты қиманың жеке орталық инерция өстеріне 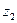 ,
, 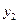 байланысты өстік инерция моменттері;
байланысты өстік инерция моменттері;
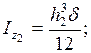
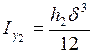
Центрден тепкіш инерция моменті
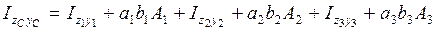
мұндағы 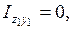
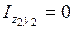 , швеллер мен тік төртбұрышты қиманың жеке орталық инерция өстеріне байланысты центрден тепкіш инерция моменттері, себебі бұл фигуралардың орталық өстерінің біреуі немесе екеуі симметрия өстері болып табылады.
, швеллер мен тік төртбұрышты қиманың жеке орталық инерция өстеріне байланысты центрден тепкіш инерция моменттері, себебі бұл фигуралардың орталық өстерінің біреуі немесе екеуі симметрия өстері болып табылады.
Тең бүйірлі бұрыштаманың жеке орталық инерция өстеріне 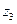 ,
, 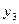 байланысты центрден тепкіш инерция моменті:
байланысты центрден тепкіш инерция моменті:
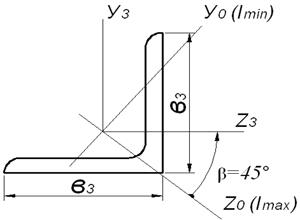
Сурет 9 – Тең бүйірлі бұрыштаманың центрден тепкіш
инерция моментін анықтауға арналған сұлба
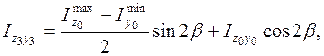 (4.8)
(4.8)
мұндағы 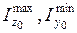 - тең бүйірлі бұрыштаманың басты орталық инерция өстері
- тең бүйірлі бұрыштаманың басты орталық инерция өстері 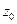 ,
, 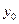 байланысты өстік инерция моментерінің мәндері;
байланысты өстік инерция моментерінің мәндері;
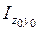 - тең бүйірлі бұрыштаманың басты орталық өстеріне
- тең бүйірлі бұрыштаманың басты орталық өстеріне 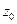 ,
, 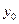 байланысты центрден тепкіш инерция моменті;
байланысты центрден тепкіш инерция моменті; 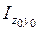 = 0 себебі
= 0 себебі 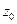 өсі тең бүйірлі бұрыштама үшін симметрия өсі;
өсі тең бүйірлі бұрыштама үшін симметрия өсі;
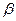 - тең бүйірлі бұрыштаманың орталық өстерінің
- тең бүйірлі бұрыштаманың орталық өстерінің 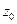 мен
мен 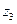 арасындағы бұрыш.
арасындағы бұрыш.
Тең бүйірлі бұрыштаманың басты орталық инерция өстерінің орындарын анықтау үшін 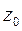 өсін
өсін 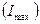
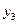 өсінен оңға қарай бағыттау керек.
өсінен оңға қарай бағыттау керек.
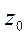 өсін
өсін 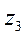 өсімен беттестіру үшін сағат тіліне қарсы бағытта бұру қажет. Сондықтан
өсімен беттестіру үшін сағат тіліне қарсы бағытта бұру қажет. Сондықтан 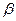 мәні оң, яғни
мәні оң, яғни 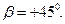
Демек,
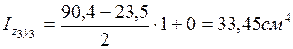
Онда күрделі қиманың центрден тепкіш моментті
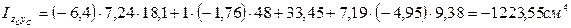
Басты орталық инерция өстерінің орындары
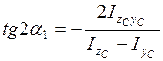 (4.9)
(4.9)
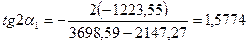 ,
,
Осыдан 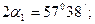
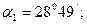
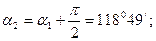
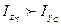 , болғандықтан,
, болғандықтан, 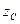 мен
мен 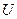 өстерінің арасындағы бұрыш
өстерінің арасындағы бұрыш 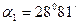 тең, яғни өсіне байланысты өстік инерция моментінің мәні максимум.
тең, яғни өсіне байланысты өстік инерция моментінің мәні максимум. 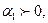 оң. Сондықтан оның мәнін
оң. Сондықтан оның мәнін 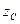 өсінен сағат тіліне қарсы бағытта салып, сызбада
өсінен сағат тіліне қарсы бағытта салып, сызбада 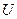 және
және 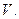 өстерін жүргіземіз.
өстерін жүргіземіз.
Басты инерция моменттері:
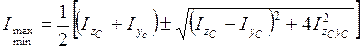 (4.10)
(4.10)
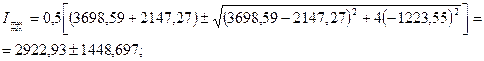
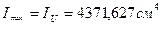 ;
; 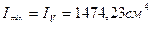
Басты инерция моменттерінің мәндерінің және басты орталық инерция өстерінің орындарының дұрыс анықталуын тексеру үшін қиманың 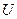 және
және 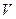 өстеріне байланысты центрден тепкіш инерция моментін есептейміз.
өстеріне байланысты центрден тепкіш инерция моментін есептейміз.
1. Егер 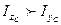
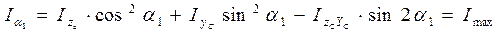
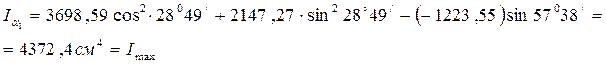 2.
2.