Атты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысы

Қозғалмайтын өсті айнала қозғалатын дене деп, екі нүктесі қозғалмайтын денені айтамыз. Қозғалмайтын нүктелерді қосатын түзу оның айналу өсі болады.

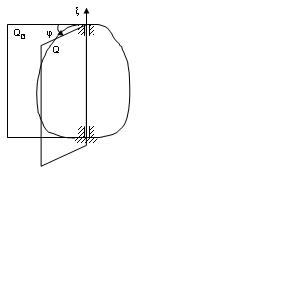
Қозғалмайтын Q_о және Q жазықтықтарының арасындағы екі жақты бұрыш φ қатты дененің айналу бұрышы деп аталады. Бұл бұрыш берілген дененің кез келген уақыт мезгіліндегі орнын бірмәнді анықтайды. Демек, қозғалмайтын өсті айналатын қатты дененің бір ғана еркіндік дәрежесі болады. Дененің қозғалмайтын өс төңірегіндегі орны бір параметрмен анықталады. Мұндай параметр ролін φ бұрышы атқарады. Ол уақыттың бірмәнді функциясы болып келеді.

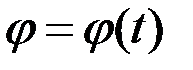. (2.61)

Бұл (2.61) теңдеуі қатты дененің айналу заңы немесе айналу теңдеуі деп аталады.

Айналу бұрышы 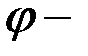дің таңбасын анықтауда оң бұранда ережесіне сүйенеміз. Егер 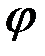бұрышы, айналу өсі 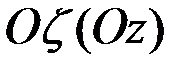-оң ұшынан қарағанда қозғалмайтын 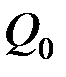жарты жазықтықтан 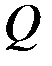жарты жазықтыққа қарай сағат тілінің қозғалысына қарсы бағытта саналатын болса, айналу бұрышын оң таңбалы деп санаймыз. Ал егер ол кері бағытпен анықталса оны “-” таңбамен алуымыз керек. Айналу бұрышы үнемі радианмен өлшенеді.

2.15-сурет

Дененің қозғалмайтын өсті айналуын сипаттауға қажетті екінші бір кинематикалық шаманы бұрыштық жылдамдық деп атайды. Оның алгебралық шамасы ω әрпімен белгіленеді. Бұрыштық жылдамдық ω дененің айналу бұрышы φ-дің уақыттың өтуіне қарай өзгеру тездігін белгілейтін шама. Алдымен белгілі бір уақыт аралығына сәйкес келетін айналу бұрышының өзгеруін қарастырайық. Егер оның t уақытына сәйкес мәні φ(t) –болсын, ал уақыттың t₁ =t+Δt мезгіліндегі мәні φ(t+Δt) болсын. Демек Δt уақыт аралығында дене Δφ бұрышына айналыс жасайды:

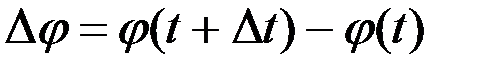(2.62)

осындағы айналу бұрышының өсімшесі (2.62)-нің оған сәйкес келетін уақыт өсімшесі Δt -ға қатынасын құрайық та, оны ω_орт деп белгілейік:

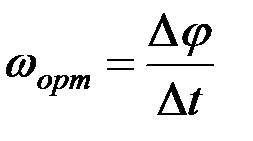. (2.63)

ω_орт орташа бұрыштық жылдамдығы деп атайды. (2.63)-тің екі жағында Δt→0 кездегі шегі:

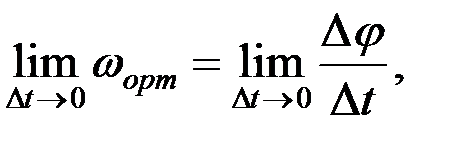
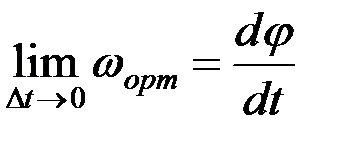. (2.64)

(2.64)-тің оң жағындағы шек φ(t) функциясының туындысын береді.

Ал оның сол жағындағы шек дененің берілген t уақыт мезгіліндегі бұрыштық жылдамдығы ω-ны береді. Осы түсіндірмелерді қабылдап (2.64) теңдігін мына түрде жазамыз:

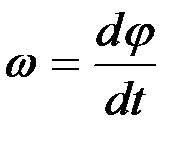. (2.65)

Бұрыштық жылдамдық векторлық шама. 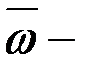векторы дененің айналу өсінің бойында орналасып, оң бұранда ережесіне сәйкес келетін бағытпен бағытталады.

Жоғарыда айтылған φ бұрышын санаудың оң бағыты жөніндегі анықтаманы ескере отырып, бұрыштық жылдамдық векторын мынадай формуламен өрнектеуге болады:

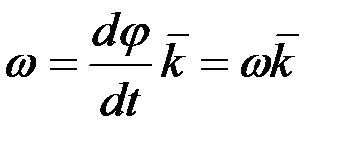, (2.66)

мұндағы 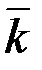, 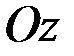өсінің бірлік векторы.

Дененің айналмалы қозғалысын сипаттаушы үшінші кинематикалық шама, бұрыштық үдеу ұғымына тоқтап өтейік. Алдымен орташа бұрыштық үдеуді анықтаймыз. Берілген t уақыт мезгіліндегі айналмалы қозғалыстың бұрыштық жылдамдығы ω(t) болсын, ал t+Δt уақыт мезгілінде ол ω(t+Δt) болсын дейік. Сонда Δt уақыт аралығында бұрыштық жылдамдық өсімшесі мынаған тең болады:

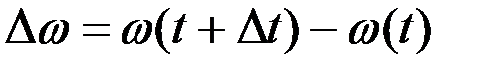. (2.67)

Осы шамалар қатынасын дененің Δt уақыты аралығындағы орташа бұрыштық үдеу деп атап, оны ε_орт әрпімен белгілейміз:

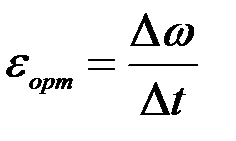. (2.68)

Бұл қатынасты пайдалана отырып, дененің берілген уақыт t мезгіліндегі, яғни лездік бұрыштық үдеудің анықтамасын бере аламыз.

Берілген уақыттағы бұрыштық үдеу деп орташа бұрыштық үдеудің Δt→0 кездегі үдеудің шегін айтамыз. Бұрыштық үдеуді ε-деп белгілесек, айтылған анықтама мына формуламен беріледі:

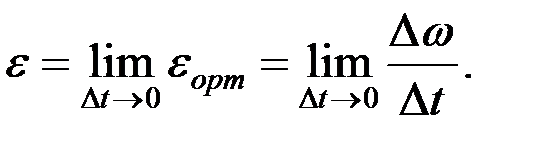(2.69)

(2.69) –теңдіктің оң жағында ω(t) функциясының уақыт бойынша алынған туындысы тұрғанын ескерсек, оны мына түрде қайталап жаза аламыз:

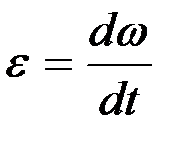немесе 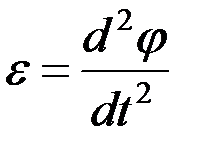. (2.70)

Бұрыштық үдеу бұрыштық жылдамдықтан уақыт бойынша алынған бірінші туындыға тең, немесе φ айналу бұрышынан уақыт бойынша алынған екінші туындыға тең болатын шама. Бұрыштық үдеу векторы 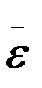де айналу өсінің бойында орналасады. Бұрыштық үдеу векторын мынадай формуламен өрнектеуге болады:

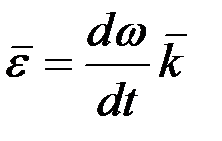немесе 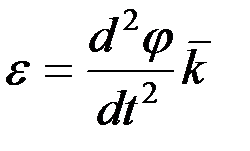. (2.71)

Бір қалыпты айналмалы және бір қалыпты айнымалы айналмалы қозғалыстар.Егер қозғалыс кезінде бұрыштық үдеу ε = 0 болса, онда қозғалыс ω = const тұрақты бұрыштық жылдамдықпен орындалады. Мұндай қозғалысты бір қалыпты айналмалы қозғалыс деп атаймыз. Осындай қозғалыстың бұрыштық жылдамдығының анықтамасынан мынадай өрнек алынады:

.

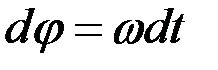Егер t₀ = 0 болғанда φ = φ₀ десек, соңғы теңдіктен мынадай формула шығады:

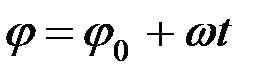. (2.72)

мұндағы бастапқы φ₀ = 0 болып келген жағдайда (2.72) –теңдіктен:

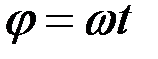және 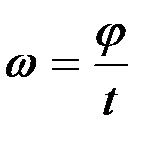. (2.73)

Дененің айналысы кезінде оның бұрыштық үдеуі ε түрақты болатын болса, онда мұндай айналмалы қозғалысты бір қалыпты айнымалы дейміз.

Бұрыштық үдеу анықтамасынан:

.

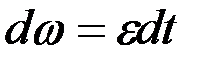Бұл теңдікті сәйкес алынған шектерде ( t₀= 0 саналады) интегралдау арқылы, мынадай формула аламыз:

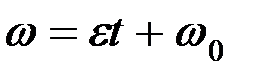. (2.74)

Бұл формуламен ε = const болған жағдайдағы бұрыштық жылдамдық анықталады. (2.74) –тің екі жағында dt-ға көбейтіп интегралдау арқылы мынадай формула аламыз:

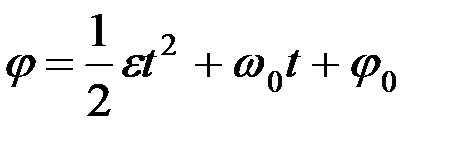. (2.75)