Вероятность гипотез. Формулы Бейеса

Следствия теорем сложения и умножения.

Формула полной вероятности

Пусть событие A может наступить при условии появления одного из несовместных событий 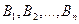, которые образуют полную группу и известны веро­ятности этих событий и условные вероятности 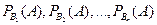события A. Как найти вероятность события A? Ответ на этот вопрос дает следующая теорема.

Теорема 5.1. Вероятность события A, которое может наступить лишь при условии появления одного из несо­вместных событий 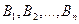, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероят­ность события А:

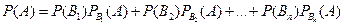(5.1)

Эту формулу называют «формулой полной вероятности».

По условию, событие A может наступить, если наступит одно из несовместных событий 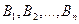. Другими словами, появление события A означает осуществление одного, безразлично какого, из несовместных событий 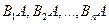. Пользуясь для вычисления вероятности события A теоремой сложе­ния, получим

(*)

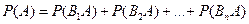По теореме умножения вероятностей зависимых событий имеем

.

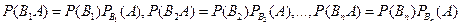Подставив правые части этих равенств в соотноше­ние (*), получим формулу полной вероятности

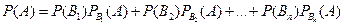
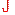
Пример. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго - 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) - стандартная.

Решение. Обозначим через А событие - «извлеченная деталь стандартна».

Гипотеза 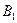- деталь извлечена из первого набора.

Гипотеза 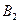- деталь извлечена из второго набора.

Вероятность того, что деталь вынута из первого набора, 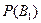= 0,5.

Вероятность того, что деталь вынута из второго набора, 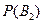= 0,5.

Условная вероятность того, что из первого набора будет извле­чена стандартная деталь, 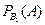= 0,8.

Условная вероятность того, что из второго набора будет извле­чена стандартная деталь, 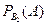= 0,9.

Искомая вероятность того, что извлеченная наудачу деталь — стандартная, по формуле полной вероятности равна

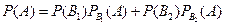= 0,5 0,8 + 0,5 0,9 = 0,85.

Вероятность гипотез. Формулы Бейеса

Пусть событие A может наступить при условии появления одного из несовместных событий 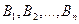, образующих полную группу. Поскольку заранее не из­вестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А опреде­ляется по формуле полной вероятности :

. (*)

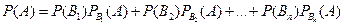Допустим, что произведено испытание, в результате которого появилось событие А. Определим, как изменились вероятности гипотез в связи с тем, что событие A уже наступило. Другими словами, будем искать условные вероятности

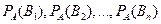
Найдем условную вероятность 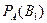. По теореме умножения имеем

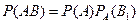
Отсюда, заменив здесь P (А) по формуле (*), получим

.

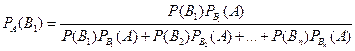Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы 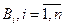может быть вычислена по формуле

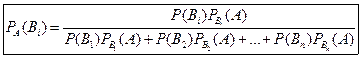(5.2)

Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как ста­новится известным результат испытания, в итоге кото­рого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Веро­ятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму - 0,4. Вероятность того, что годная деталь будет приз­нана стандартной первым контролером, равна 0,94, а вторым - 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предполо­жения:

1) деталь проверил первый контролер (гипотеза );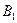

2) деталь проверил второй контролер (гипотеза ).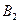

Искомую вероятность найдем по формуле Бейеса: .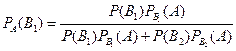

По условию задачи имеем:

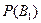= 0,6 (вероятность того, что деталь попадает к первому контролеру);

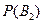= 0,4 (вероятность того, что деталь попадет ко второму контролеру);

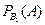= 0,94 (вероятность того, что годная деталь будет признана

стандартной первым контролером);

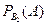= 0,98 (вероятность того, что годная деталь будет признана

стандартной вторым контролером).

Искомая вероятность

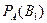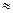= (0,6 0,94)/(0,6 0,94 + 0,4 0,98) 0,59.

Как видно, до испытания вероятность гипотезы 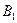равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала рав­ней 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.

Формула Бернулли

Если производится несколько испытаний, при­чем вероятность события A в каждом испытании не за­висит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

В разных независимых испытаниях событие A может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие A имеет одну и ту же вероятность.

Ниже воспользуемся понятием сложного события, по­нимая под ним совмещение нескольких отдельных собы­тий, которые называют простыми.

Пусть производится n независимых испытаний, в каж­дом из которых событие A может появиться либо не появиться. Условимся считать, что вероятность собы­тия A в каждом испытании одна и та же и равна р. Следовательно, вероятность не наступления со­бытия A в каждом испытании также постоянна и равна q = 1 - p.

Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие A осуществится ровно k раз и, следовательно, не осуществится n - k раз. Важно подчеркнуть, что не требуется, чтобы событие A повторилось ровно k раз в определенной последовательности. Например, если событие A появилось три раза в четырех испытаниях, то возможны следующие сложные события: 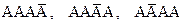, 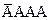. Запись 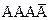означает, что в первом, втором и третьем испы­таниях событие A наступило, а в четвертом испытании оно не появилось, т. е. наступило противоположное со­бытие A; соответственный смысл имеют и другие записи.

Искомую вероятность обозначим 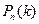. Например, символ 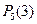означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и не наступит 2 раза.

Поставленную задачу можно решить с помощью формулы Бернулли.

Вывод формулы Бернулли. Вероятность слож­ного события, состоящего в том, что в n испытаниях событие A наступит k раз и не наступит n - k раз, по теореме умножения вероятностей независимых событий равна 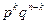. Таких сложных событий может быть столько, сколько можно составить сочетаний из n эле­ментов по k элементов 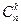. Так как эти сложные события несовместны, то по теореме сложения вероятно­стей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз со­бытия А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:

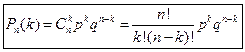. (5.3)

Полученную формулу называют формулой Бернулли.

Пример. Вероятность того, что расход электроэнергии в продол­жение одних суток не превысит установленной нормы, равна p = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электро­энергии в течение 4 суток не превысит нормы.

Решение.

Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна p = 0,75. Сле­довательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 – p = 1 - 0,75 = 0,25.

Искомая вероятность по формуле Бернулли равна

.

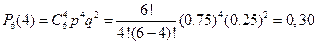Пример. Вероятность наступления события в каждом из 7 независимых испытаний равна p = 0,7. Найти P(3<m<6), P(m<6) по формуле Бернулли.

Решение

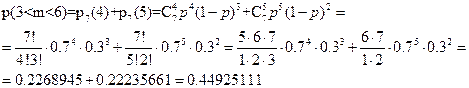
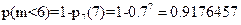
Ответ: 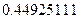, .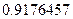