Векторный потенциал
Векторный потенциал 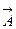 (М) определяется с точностью до градиента произвольного соленоидального поля f(М).
(М) определяется с точностью до градиента произвольного соленоидального поля f(М).
В самом деле, если rot 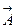 (М)=
(М)= 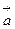 (М) и f(M) – произвольное скалярное поле, то поскольку rot grad f(M)=0, получаем rot(
(М) и f(M) – произвольное скалярное поле, то поскольку rot grad f(M)=0, получаем rot( 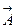 (М)+grad f(M)) = rot
(М)+grad f(M)) = rot 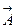 (М)+ rot grad f(M)=
(М)+ rot grad f(M)= 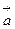 (М).
(М).
Для того чтобы непрерывно дифференцируемое поле 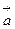 (М) было соленоидальным, необходимо и достаточно, чтобы оно имело векторный потенциал
(М) было соленоидальным, необходимо и достаточно, чтобы оно имело векторный потенциал 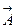 (М). Необходимость этого условия является следствием разрешимости системы дифференциальных уравнений:
(М). Необходимость этого условия является следствием разрешимости системы дифференциальных уравнений:
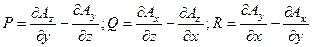 (1)
(1)
при условии div 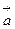 =0 (
=0 ( 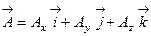 ).
).
Покажем как можно найти векторный потенциал 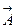 (М). поскольку в выборе этого вектора имеется значительная доля произвола примем Ax=0. Тогда система (1) примет вид
(М). поскольку в выборе этого вектора имеется значительная доля произвола примем Ax=0. Тогда система (1) примет вид
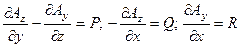 (2)
(2)
Таким образом, задача сводиться к определению функции Ay и Az, удовлетворяющих условиям (2) при условии, что известные функции P, Q, R таковы, что div  =0. Пусть М0(x0,y0,z0) – фиксированная, М(x,y,z) – произвольные точки параллелепипеда W.
=0. Пусть М0(x0,y0,z0) – фиксированная, М(x,y,z) – произвольные точки параллелепипеда W.
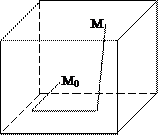 |
Рис. 6.
Рассмотрим функции
Ay(x,y,z)= 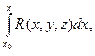 Az(x,y,z)=
Az(x,y,z)= 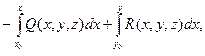 (3)
(3)
Условие задания поля 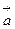 (М) в параллелепипеде с гранями, параллельными плоскостям координат, гарантирует, что пути интегрирования в этих формулах не выйдут за пределы поля. Применяя правила дифференцирования определенного интеграла по параметру и по верхнему пределу и принимая во внимание условие div
(М) в параллелепипеде с гранями, параллельными плоскостям координат, гарантирует, что пути интегрирования в этих формулах не выйдут за пределы поля. Применяя правила дифференцирования определенного интеграла по параметру и по верхнему пределу и принимая во внимание условие div 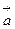 =0 , получим , что обе функции Ay и Az, определенные равенствами (3) удовлетворяют и первому из условий (2). Таким образом,
=0 , получим , что обе функции Ay и Az, определенные равенствами (3) удовлетворяют и первому из условий (2). Таким образом, 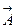 = Ах
= Ах 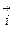 + Ay
+ Ay 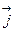 +Az
+Az 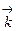 , координаты Ay и Az определяются формулами (3). Для этого вектора
, координаты Ay и Az определяются формулами (3). Для этого вектора 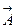 выполняется условие rot
выполняется условие rot 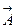 =
= 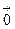 .
.
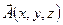 |
74. Найти векторный потенцал
для соленоидального поля, задаваемого вектором а = 2уi - zj + 2хk.
Ответы:
10. Область определения – круг x2+y2£9; линии уровня – семейство концентрических окружностей
x2+y2=9–с2 (|с| £ 3).
11. Поле определено во всем пространстве, за исключением точки r=0; поверхности уровня –сферы r=c c центром в точке, где находится заряд.
12.Поле определено в области z2+y2–x2³0;поверхности уровня – круговые конусы а2(z2+y2)–x2=0 (|а| £ 1).
13. Линии уровня u=c представляют собой семейство гипербол x2–y2=(–1)n arcsin c +pn, где n–целое число.
14. Поле определено во всем пространстве, за исключением плоскости z=0; поверхности уровня – параболоиды вращения x2 +y2=сz (–¥<c<¥).
15. а) –4 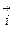 +2
+2 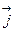 –4
–4 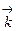 . б) 12
. б) 12 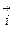 –
– 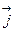 ; в)
; в) 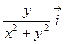 +
+ 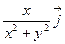 .
.
16. Прямые, проходящие через начало координат.
17. x2 -y2=с; z=h.
18. x3 +y3=c1; z3 +y3=c2.
19. y=c1z; x2 +y2+ z2= c2y.
20. Окружности, лежащие в плоскостях, перпендикулярных к прямой, проходящей через начало координат и имеющей направление вектора 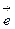 ; центры этих окружностей лежат на этой прямой.
; центры этих окружностей лежат на этой прямой.
22. Окружности с центром на оси Оy , проходящей через начало координат.
23. Направление наибыстрейшего возрастания функции в точке (0,0) совпадает с положительным направлением оси Оy.
24. 1) tgj »0,342, j »18052’; 2) tgj »4,87, j »78024’.
25. Отрицательная полуось оси Оy.
26. 1) cosa »0,99; a=80; 2) cosa » –0,199; a=101030’;
30. Ц= –pb2.
31. Ц= –p.
32. Ц= 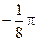 R6
R6
33. а) Ц=2p; б) Y=2p.
39. 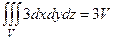 .
.
40. 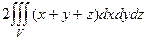
41.0.
42. 4pabc.
43. 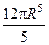 .
.
44. 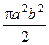 .
.
45. 1.
46. 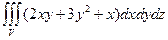 .
.
47. 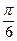 .
.
48. a) 4pa3; б) 0. Дополните поверхность S до замкнутой; в)0; г) p. Дополните поверхность S до замкнутой; д)0; е) 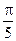 ; ж) 3а4.
; ж) 3а4.
52. 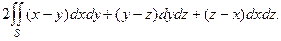
53. 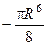 .
.
60. а) rot 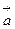 = –2cos(2x–y–z)(
= –2cos(2x–y–z)( 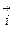 +2
+2 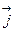 ); б) rot
); б) rot 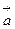 =x(z2-y2)
=x(z2-y2) 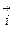 + y(x2-z2)
+ y(x2-z2) 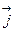 + z(y2-x2)
+ z(y2-x2) 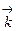 ; в) rot
; в) rot 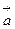 =
= 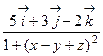 .
.
61. 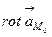 =20
=20 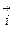 +26
+26 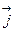 –24
–24 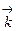 .
.
62. 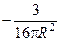 .
.
63.–2a2 .
64. а) Ц=2p; б) Ц=0.
68. 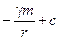 .
.
69. 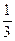 (x3+2y3+z3)+3xyz + c.
(x3+2y3+z3)+3xyz + c.
70. 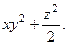
71. Нет.
72. Потенциальными являются поля 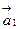 и
и 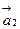 .
.
73. 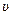 (x,y,z)=xyz(x+y+z)+c, где с произвольная постоянная.
(x,y,z)=xyz(x+y+z)+c, где с произвольная постоянная.
74. х2j + (хz + y2)k.
Литература
1. Государственный образовательный стандарт высшего профессионального образования. М.: Госкомвуз России, 2000.
2. Никольский С.М. Курс математического анализа, том. II- М.: Наука, 1973.
3. Зорич В.А. Математический анализ. Ч. II.- М.: Наука, 1984
4. Уваров В.Б. Математический анализ. М.: Высш.шк.,1984.
5. Ефимов А.В. и др. Математический анализ (специальные разделы) ч.II. Применение некоторых методов математического и функционального анализа. - М.: Высш. шк., 1980.
6. Кальницкий Л.А и др. Специальный курс высшей математики для вутзов. М.: Высш. шк., 1976.
7. Несис Е.И. Методы математической физики. - М.: Просвещение, 1977.
8. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, 1972.
9. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1985.
10. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах. Функции нескольких переменных. - М.: Высш. шк. ,1988.
11. Филиппенко В.И. Приложения кратных интегралов. – Кривой Рог, 1998.
12. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. – М.: Изд – во МГТУ им. Н.Э.Баумана, 2001.
