Пример расчета НДС балочного перехода с учетом его совместной деформации с прилегающими подземными участками
Напряженно-деформированное состояние однопролетного бескомпенсаторного надземного перехода газопровода с учетом совместной деформации с прилегающими подземными участками
Постановка задачи
В предыдущем разделе для упрощения анализа влияния параметров эксплуатации перехода на его НДС пренебрегалось совместной деформацией перехода с прилегающими подземными участками. В данном параграфе выявим влияние совместной деформации на характеристики НДС газопровода.
На рисунке 2.3 представлена расчетная схема нагружения перехода, которая состоит из 3 – х условных частей: средняя надземная часть и две подземные, прилегающие слева и справа, части.
Рассмотрим 3 варианта постановки задачи о НДС перехода, которые были подробно описаны в п. 2.2. НДС надземной части для первого, второго и третьего варианта описывают уравнения (2.16), (2.34) и (2.45), соответственно. Общее решение этих уравнений с учетом условия симметричного нагружения надземной части перехода имеет вид (2.19), (2.36) и (2.49), соответственно.
В подземных частях трубопровод совместно деформируется с грунтом под действием собственно веса с газом, давление грунта засыпки, которое зависит от наличия свода естественного равновесия грунта засыпки [19,20]. Грунт основания в упругой области его деформации моделируется основанием Винклера, а в упруго-пластической области деформации применяется метод переменных параметров упругости, аналогичный методу упругих решений при исследовании упругопластической работы металла.
Первый вариант постановки задачи и его решение
В случае защемления концов подземных участков их НДС описывается следующим уравнением
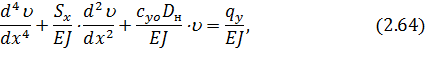
где 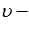 прогиб трубопровода;
прогиб трубопровода;
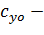 обобщенный коэффициент нормального сопротивления грунта, связанный с модулем деформации грунта зависимостью
обобщенный коэффициент нормального сопротивления грунта, связанный с модулем деформации грунта зависимостью
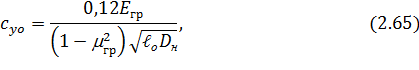
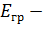 модуль деформации грунта;
модуль деформации грунта;
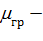 коэффициент Пуассона грунта;
коэффициент Пуассона грунта;
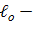 единичная длина трубопровода;
единичная длина трубопровода;
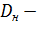 наружный диаметр трубы.
наружный диаметр трубы.
В узлах сопряжения надземной и подземных частей должны выполняться следующие граничные условия
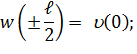
 2.66)
2.66)
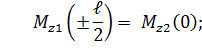
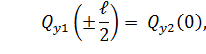
где 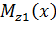 ,
, 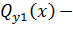 функции изгибающего момента и поперечной силы в надземной части;
функции изгибающего момента и поперечной силы в надземной части;
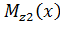 ,
, 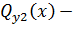 функции изгибающего момента и поперечной силы в подземных участках.
функции изгибающего момента и поперечной силы в подземных участках.
Эти условия означают непрерывность прогиба, угла поворота продольной оси, изгибающих моментов и поперечной силы надземной и подземных частей в узле их сопряжения, т.е. продольная осевая линия трубопровода представляет собой непрерывную главную линию, не имеющую изломов.
Общее решение уравнения (2.64) с учетом его затухания на концах подземных участков можно представить в следующем виде
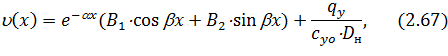
где 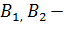 постоянные интегрирования;
постоянные интегрирования;
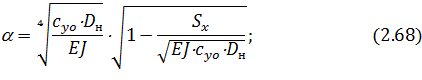
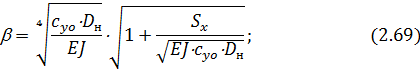
Далее находим 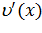 ,
, 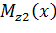 и
и 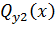
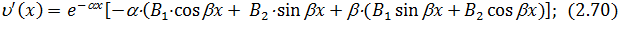
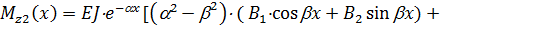

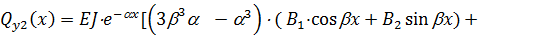
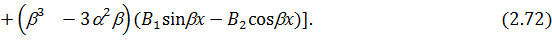
Находя значения функций (2.19) – (2.23) при 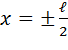 для надземной части и значения функций (2.67), (2.70) – (2.72) при
для надземной части и значения функций (2.67), (2.70) – (2.72) при 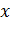 =0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются
=0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются  .
.
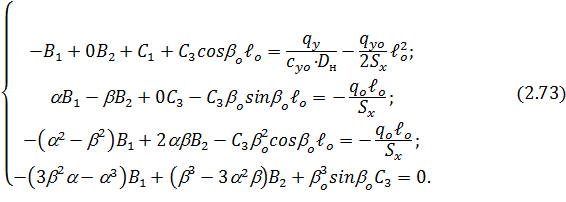
Второй вариант постановки задачи и его решение
В данном случае пренебрегаем воздействием внутреннего рабочего давления и температурных напряжений, которые вызывают дополнительный изгиб трубопровода, т.е. эквивалентное продольное усилие 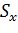 принимаем равным 0
принимаем равным 0 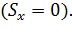
НДС надземной части описывается уравнением (2.34), а подземных частей – уравнением

где 
Уравнение (2.74) совпадает с уравнением балки на упругом основании или стержне в упругой среде классической теории стержней. С учетом условия затухания его решения на концах подземных частей решение уравнения (2.74) можно представить в следующем виде
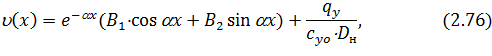
где 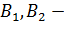 постоянные интегрирования.
постоянные интегрирования.
Далее, используя (2.76) находим 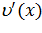 ,
, 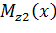 и
и 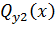 .
.
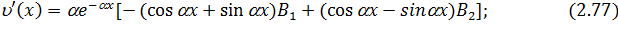
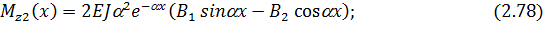
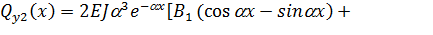
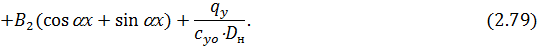
Находя значения функций (2.37) – (2.40) при 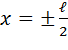 для надземной части и значения функций (2.76) – (2.79) при
для надземной части и значения функций (2.76) – (2.79) при 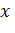 = 0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются
= 0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются
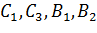 .
.
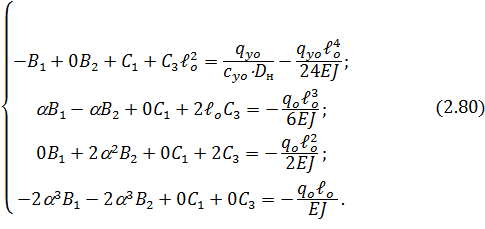
Третий вариант постановки задачи и его решения
В данном случае трубопровод растягивается при изгибе под воздействием внутреннего рабочего давления на закрытую задвижку или заглушку (модель компенсатора), находящейся на одном из концов подземного участка, например, правого участка. Левый конец левой подземной части защемлен грунтом и не может перемещаться в продольном направлении.
НДС надземной части описывается с помощью уравнения (2.45), а подземных частей уравнением (2.81)
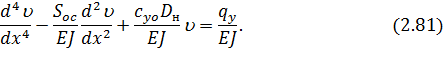
С учетом условия затухания решение уравнения (2.81) можно представить в следующем виде
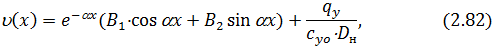
где
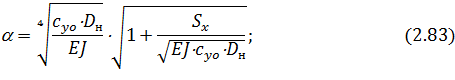
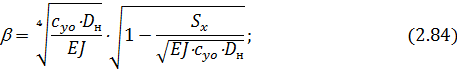
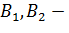 постоянные интегрирования.
постоянные интегрирования.
Далее, используя (2.76) находим 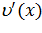 ,
, 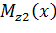 и
и 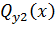 .
.
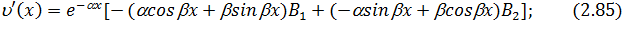
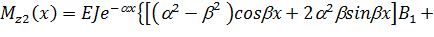
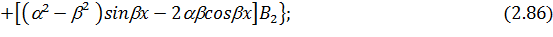
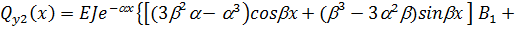
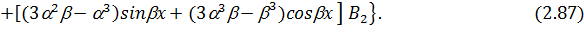
Находя значения функций (2.49) и её производных при 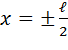 для надземной части и значения функций (2.82), (2.85) – (2.87) при
для надземной части и значения функций (2.82), (2.85) – (2.87) при 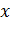 =0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются
=0 для подземных частей и подставляя их в граничные условия (2.66), получим следующую систему четырех линейных алгебраических уравнений, где неизвестными являются 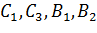 .
.
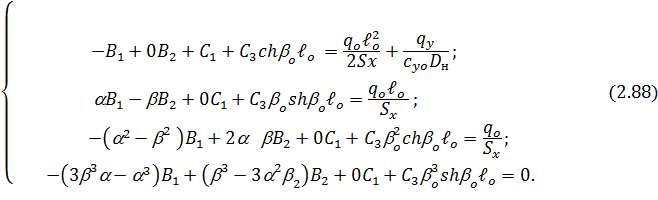
Для решения систем линейных алгебраических уравнений (2.73), (2.80), (2.88) методом Гаусса, а также для расчета основных характеристик НДС трубопровода (прогиба, угла поворота продольной оси трубы, изгибных напряжений, поперечной силы) для надземной и подземных частей перехода составлена программа для компьютера. Эта же программа позволяет построить эпюры основных характеристик НДС по всей длине рассчитываемого участка для всех трех вариантов постановки задачи.
Пример расчета НДС балочного перехода с учетом его совместной деформации с прилегающими подземными участками
Приведем пример расчета НДС балочного перехода длиной 59,3 м с учетом его совместной деформации с прилегающими подземными участками. Были рассмотрены два типа грунта, которые имеют следующие значения физико-механических характеристик:
грунт жесткий с модулем деформации 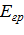 = 40 МПа, коэффициентом Пуассона
= 40 МПа, коэффициентом Пуассона 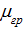 =0,2;
=0,2;
грунт мягкий ослабленный с модулем деформации 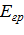 - 10 МПа, коэффициентом Пуассона
- 10 МПа, коэффициентом Пуассона 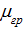 = 0,4;
= 0,4;
высота засыпки грунта соответствует проектной.
Остальные исходные и расчетно-исходные данные аналогичны данным примера расчета п.2.2.1, где не учитывалась совместная деформация надземной и подземных частей.
На рисунках 2.10, 2.11 представлены эпюры основных характеристик НДС перехода: поперечной силы, изгибных напряжений поворота продольной оси трубы и прогиба для всех трех вариантов постановки задачи. Обозначения эпюр для первой, второй, третьей постановок задачи аналогичны предыдущей задачи.
Представленные на рисунках 2.10, 2.11 эпюры прогибов 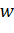 , углов поворота нормали
, углов поворота нормали 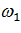 продольной оси трубопровода при его совместной деформации с грунтом, а также изгибных напряжений
продольной оси трубопровода при его совместной деформации с грунтом, а также изгибных напряжений 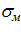 и перерезывающих сил
и перерезывающих сил 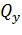 построены по результатам совместного решения уравнений, описывающих НДС надземной и подземных частей перехода.
построены по результатам совместного решения уравнений, описывающих НДС надземной и подземных частей перехода.
Функции 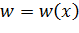 ,
, 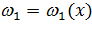 ,
, 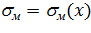 и
и 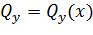 связаны между собой дифференциальными зависимостями для надземного и подводных участков условного разбиения рассчитываемого участка трубопровода. Эта связь сохраняется и после совместного интегрирования уравнений, описывающих НДС этих участков, что иллюстрируют графики функций
связаны между собой дифференциальными зависимостями для надземного и подводных участков условного разбиения рассчитываемого участка трубопровода. Эта связь сохраняется и после совместного интегрирования уравнений, описывающих НДС этих участков, что иллюстрируют графики функций 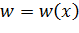 ,
, 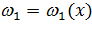 ,
, 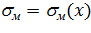 и
и 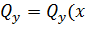 ), представленные в виде эпюр рисунков 2.10, 2.11. В частности, там, где функция прогибов
), представленные в виде эпюр рисунков 2.10, 2.11. В частности, там, где функция прогибов 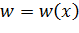 достигает по переменной
достигает по переменной 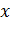 экстремальных значений, функция угла поворота нормали
экстремальных значений, функция угла поворота нормали 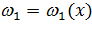 пересекает ось ОХ, т.к. она определяется через
пересекает ось ОХ, т.к. она определяется через




Рисунок 2.10 – Расчет основных характеристик НДС балочного перехода газопровода в жестком грунте (l0=59,3 м, Egr=40 МПа, p0= 7,5 МПа, dt=40 0C, Sx=7110 кН, Sp=6369 кН, Nx= - 675,3 кН): поперечной силы, изгибных напряжений, угла поворота продольной оси трубы, прогиба




Рисунок 2.11 – Расчет основных характеристик НДС балочного перехода газопровода в мягком ослабленном грунте (l0=59,3 м, Egr=10 МПа, p0= 7,5 МПа, dt=40 0C, Sx=7110 кН, Sp=6369 кН, Nx= - 675,3 кН): поперечной силы, изгибных напряжений, угла поворота продольной оси трубы, прогиба
производную от функции 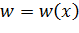 . Если прогиб
. Если прогиб 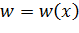 убывает, то
убывает, то 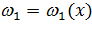 принимает отрицательные значения, а если
принимает отрицательные значения, а если 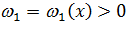 , то
, то 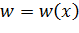 возрастает. Аналогичные зависимости выполняются между углом поворота нормали
возрастает. Аналогичные зависимости выполняются между углом поворота нормали 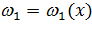 и изгибными напряжениями
и изгибными напряжениями 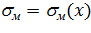 , а также между изгибными напряжениями
, а также между изгибными напряжениями 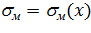 и перерезывающими силами
и перерезывающими силами 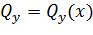 , Таким образом, основные закономерности, которые следуют из дифференциального уравнения изогнутой оси балки, сохраняются и для составной стержневой системы, моделирующей трубопровод.
, Таким образом, основные закономерности, которые следуют из дифференциального уравнения изогнутой оси балки, сохраняются и для составной стержневой системы, моделирующей трубопровод.
В таблице 2.7 приведены максимальные значения прогиба в середине пролета и изгибные напряжения от пролетных и опорных изгибающих моментов для жесткого грунта ( 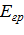 = 40 МПа,
= 40 МПа, 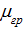 =0,2).
=0,2).
Таблица 2.7 – Максимальные значения прогиба и значения изгибных напряжений от пролетных и опорных изгибающих моментов ( 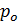 =7,5 МПа,
=7,5 МПа, 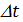 = 40оС)
= 40оС)
| Вариант постановки задачи | Прогиб, см | Изгибные напряжения , МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | 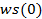 = - 75,8 = - 75,8 | 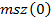 =429,1 =429,1 | 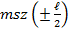 =-467,0 =-467,0 |
| Второй | 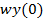 = - 24,2 = - 24,2 | 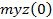 = 117,5 = 117,5 | 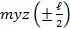 =-164,3 =-164,3 |
| третий | 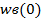 = - 15,2 = - 15,2 | 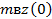 =66,6 =66,6 | 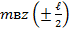 = -109,5 = -109,5 |
Анализ данных таблицы 2.7 показывает, что воздействие внутреннего рабочего давления и температурных напряжений приводит к увеличению прогиба в 3 раза, к увеличению изгибных напряжений от пролетных изгибающих моментов в 3,5 раза, к увеличению изгибных напряжений от опорных изгибающих моментов в 3 раза.
Растяжение трубопровода под воздействием внутреннего рабочего давления на закрытую задвижку (заглушку), которая моделирует работу компенсатора, приводит к уменьшению максимального значения прогиба в середине пролета в 5 раз, изгибных напряжений от пролетных – в 6 раз, опорных изгибающих моментов – в 4,5 раза.
В таблице 2.8 приведены максимальные значения прогиба в середине пролета и изгибные напряжения от пролетных и опорных изгибающих моментов для мягкого ослабленного грунта ( 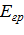 = 10 МПа,
= 10 МПа, 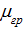 =0,4).
=0,4).
Таблица 2.8 – Максимальные значения прогиба и значения изгибных напряжений от пролетных и опорных изгибающих моментов ( 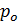 =7,5 МПа,
=7,5 МПа, 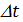 = 40оС)
= 40оС)
| Вариант постановки задачи | Прогиб, см | Изгибные напряжения , МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | 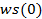 = - 112,9 = - 112,9 | 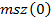 = 580,3 = 580,3 | 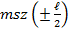 =-571,3 =-571,3 |
| Второй | 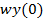 = - 30,8 = - 30,8 | 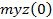 = 128,8 = 128,8 | 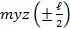 =-158,8 =-158,8 |
| третий | 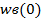 = - 19,6 = - 19,6 | 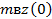 = 70,5 = 70,5 | 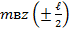 = -91,6 = -91,6 |
Анализ данных таблицы 2.8 показывает, что воздействие внутреннего рабочего давления и температурных напряжений приводит к увеличению прогиба в 3,5 раза, к увеличению изгибных напряжений от пролетных изгибающих моментов в 4,5 раза, к увеличению изгибных напряжений от
опорных изгибающих моментов в 3,5 раза.
Растяжение трубопровода под воздействием внутреннего рабочего давления на закрытую задвижку (заглушку), которая моделирует работу компенсатора, приводит к уменьшению максимального значения прогиба в середине пролета в 6 раз, изгибных напряжений от пролетных – в 8 раз, опорных изгибающих моментов – в 6 раз.
Выполненный анализ НДС перехода показывает, что при ослаблении жесткости основания в прилегающих участках воздействия давления и температурных напряжений на изгиб трубопровода становится определяющим. Трубопровод испытывает чрезмерные изгибные напряжения, соизмеримые с кольцевыми от внутреннего рабочего давления и может разрушиться раньше, чем наступит его потеря устойчивости. Степень воздействия внутреннего рабочего давления и температурных напряжений на изгиб трубопровода, кроме жесткости основания, зависит и от длины пролета надземной части перехода. Для иллюстрации этого представим результаты расчета НДС перехода с длиной надземной части в 2 раза меньше. Чем в предыдущем анализе 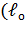 =29,65 м). На рисунках 2.12, 2.13 представлены основные характеристики НДС перехода с длиной
=29,65 м). На рисунках 2.12, 2.13 представлены основные характеристики НДС перехода с длиной 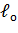 =29,65 м для жесткого грунта основания (рисунок 2.12) и для мягкого ослабленного (рисунок 2.13).
=29,65 м для жесткого грунта основания (рисунок 2.12) и для мягкого ослабленного (рисунок 2.13).
В таблице 2.9 приведены максимальные значения прогиба в середине пролета и изгибные напряжения от пролетных и опорных изгибающих моментов для жесткого грунта ( 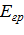 = 40 МПа,
= 40 МПа, 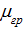 =0,2,
=0,2, 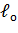 =29,65 м).
=29,65 м).
Таблица 2.9 – Максимальные значения прогиба и значения изгибных напряжений от пролетных и опорных изгибающих моментов ( 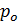 =7,5 МПа,
=7,5 МПа, 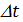 = 40оС,
= 40оС, 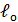 =29,65 м)
=29,65 м)
| Вариант постановки задачи | Прогиб, см | Изгибные напряжения, МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | 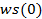 = - 3,5 = - 3,5 | 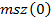 = 48,0 = 48,0 | 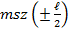 =-48,3 =-48,3 |
| Второй | 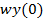 = - 2,9 = - 2,9 | 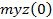 = 36,4 = 36,4 | 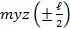 =-38,4 =-38,4 |
| третий | 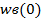 = - 2,5 = - 2,5 | 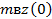 = 29,6 = 29,6 | 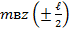 = -32,2 = -32,2 |
Анализ данных таблицы 2.9 показывает, что максимальные прогибы в середине пролета соизмеримы с толщиной стенки трубы, а изгибные напряжения от пролетных опорных изгибающих моментов по абсолютной величине примерно в 10 раз меньше, чем кольцевые напряжения от внутреннего рабочего давления. Воздействие внутреннего рабочего давления и температурных напряжений не оказывает существенного влияния на изгиб трубопровода, который сохраняет свое проектное положение.
В таблице 2.10 приведены максимальные значения прогиба в середине пролета и изгибные напряжения от пролетных и опорных изгибающих моментов для мягкого ослабленного грунта ( 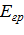 = 10 МПа,
= 10 МПа, 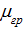 =0,4,
=0,4, 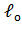 =29,65 м)
=29,65 м)




Рисунок 2.12 - Расчет основных характеристик НДС балочного перехода газопровода в жестком грунте (l0=29,65 м, Egr=40 МПа, p0= 7,5 МПа, dt=40 0C,
Sx=7110 кН, Sp=6369 кН, Nx= - 675,3 кН)




Рисунок 2.13 - Расчет основных характеристик НДС балочного перехода газопровода в мягком ослабленном (l0=29.65 м, Egr=10 МПа, p0= 75 МПа, dt=40-C, Sx=7110 кН, Sp=6369 кН, Nx= - 675,3 кН)
Таблица 2.10 – Максимальные значения прогиба и значения изгибных напряжений от пролетных и опорных изгибающих моментов ( 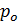 =7,5 МПа,
=7,5 МПа, 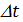 = 40оС,
= 40оС, 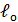 =29,65 м)
=29,65 м)
| Вариант постановки задачи | Прогиб, см | Изгибные напряжения, МПа | |
| от пролетных изгибающих моментов | от опорных изгибающих моментов | ||
| Первый | 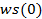 = - 6,6 = - 6,6 | 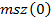 = 59,4 = 59,4 | 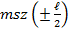 =-49,8 =-49,8 |
| Второй | 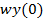 = - 5,5 = - 5,5 | 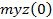 = 42,4 = 42,4 | 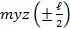 =-36,8 =-36,8 |
| третий | 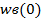 = - 4,9 = - 4,9 | 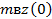 = 33,4 = 33,4 | 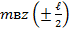 = -29,7 = -29,7 |
Анализ данных таблицы 2.10 показывает, что, как и в предыдущем случае, максимальные прогибы в середине пролета соизмеримы с толщиной стенки трубы, а изгибные напряжения от пролетных опорных изгибающих моментов по абсолютной величине примерно в 10 раз меньше, чем кольцевые напряжения от внутреннего рабочего давления. Воздействие внутреннего рабочего давления и температурных напряжений не оказывает существенного влияния на изгиб трубопровода, который сохраняет свое проектное положение.
Таким образом, для пролетов небольшой длины воздействие давления и температурных напряжений, а также уменьшение жесткости грунта основания не вызывает дополнительного изгиба трубопровода, способного нарушить его проектное положение.
