Вектор-функция скалярного аргумента. Годограф. Производная. Касательная прямая и нормальная плоскость.

Векторная функция скалярного аргумента.

A(x, y, z)

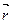
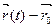
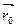
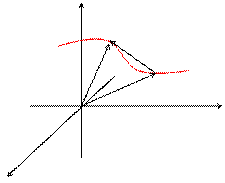
Пусть некоторая кривая в пространстве задана параметрически: x = j(t); y = y(t); z = f(t); Радиус- вектор произвольной точки кривой: .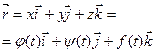

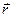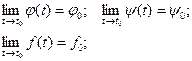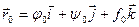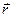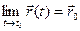Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора . Запишем соотношения для некоторой точкиt₀: Тогда вектор - предел функции (t). . Очевидно, что 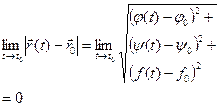, тогда 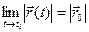. Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.

; ;

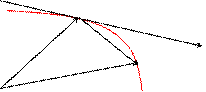
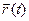
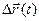
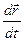
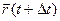
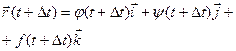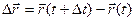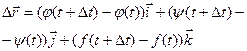
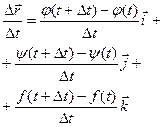
или, если существуют производные j¢(t), y¢(t), f¢(t), то .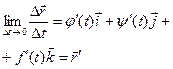

Это выражение – вектор производная вектора 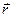. 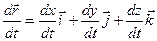; 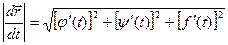. Если имеется уравнение кривой: x = j(t); y = y(t); z = f(t); то в произвольной точке кривой А(x_А, y_А, z_А) с радиус- вектором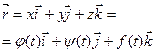

можно провести прямую с уравнением 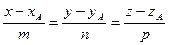. Т.к. производная 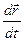- вектор, направленный по касательной к кривой, то 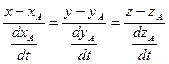. Уравнение нормальной плоскостик кривой будет иметь вид: .

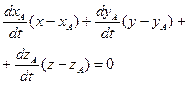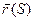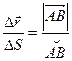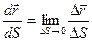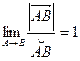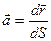Определение: Линия, которую опишет в пространстве переменный радиус – вектор при изменении параметра S, называется годографом этого вектора. , тогда - вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. , то - единичный вектор, направленный по касательной. Если принять 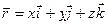, то .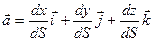

Причем 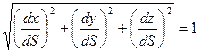. Рассмотрим вторую производную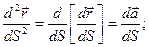

Определение: Прямая, имеющая направление вектора 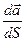называется главной нормалью к кривой. Ее единичный вектор обозначается 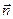. 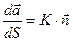, где К – кривизна кривой.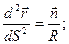

54. Кривизна и кручение. Кривизна пространственной кривой.

z

B

A(x, y, z)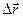

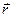
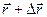
0 y

x

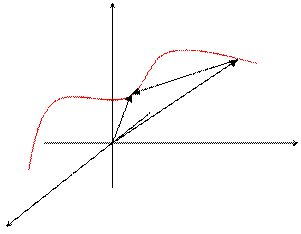
Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.

x = j(S); y = y(S); z = f(S); 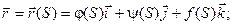Приведенное выше уравнение называют векторным уравнением линии в пространстве.

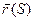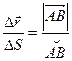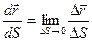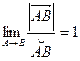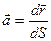Определение: Линия, которую опишет в пространстве переменный радиус – вектор при изменении параметра S, называется годографом этого вектора. , тогда - вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. , то - единичный вектор, направленный по касательной. Если принять 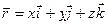, то 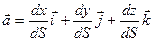. Причем 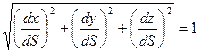. Рассмотрим вторую производную 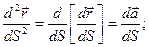Определение: Прямая, имеющая направление вектора 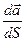называется главной нормалью к кривой. Ее единичный вектор обозначается .

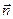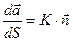, где К – кривизна кривой. 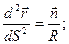Кривизна пространственной кривой может быть найдена по формуле: 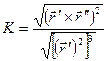Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):

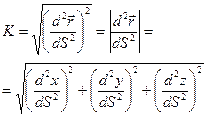Определение: Вектор 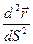называется вектором кривизны. Величина 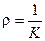называется радиусом кривизны.

Величина 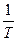называется кручением кривой.

55. Сопровождающий трёхгранник Френе. Формулы Френе.

Под трёхгранником Френе, иначе называемым естественным, сопровождающим или сопутствующим трёхгранником или репером, понимают тройку векторов 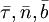сопоставленную каждой точке гладкой кривой, где — единичный касательный вектор, 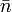— единичный вектор главной нормали, 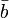— единичный вектор бинормали к кривой в данной точке. Если s — натуральный параметр вдоль кривой, то векторы 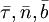вязаны соотношениями:

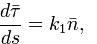
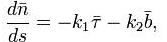
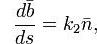
называемыми формулами Френе и задающими натуральное уравнение кривой.