Равномерная сходимость ряда

На уроке о разложении функций в степенные ряды я рассказал вам о самом понятиисходимости ряда и сейчас настал момент познакомиться с важнейшим свойствомсходящихся функциональных рядов, а именно с равномерностью сходимости. Ничего сложного в этом нет, как обычно – немного теории и обильная практика. Впрочем, «чайникам» таки лучше начать с первой статьи по теме (ссылка выше), а может быть и вообще с числовых рядов.

Сначала немного освежим воспоминания. Рассмотрим функциональный ряд
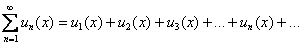и предположим, что данный ряд сходится к функции 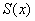на некотором промежутке (интервале, полуинтервале или каком-то другом). Что значит «сходится»?

Распишем стройную шеренгу частичных сумм. По сути дела – это тоже «обычные» функции:

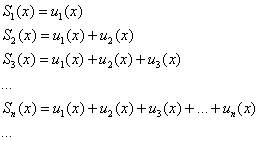
Если мы возьмём, например, функцию, состоящую из первых трёх членов ряда 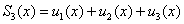, то её график (в общем случае) будет мало напоминать график функции :

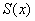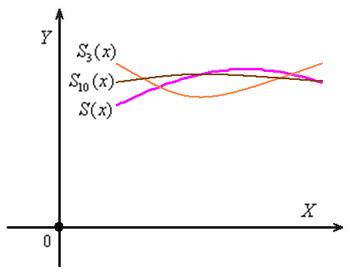
Если рассмотреть функцию из первых 10 членов ряда 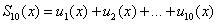, то приближение будет уже лучше. И чем больше членов ряда взять – тем ближе график 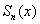приблизится к графику 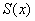. Ну а в пределе, не нужно быть провидцем:

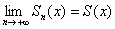
Функция 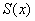называется суммой функционального ряда: 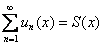, и как видите, определяется она по тому же принципу, что и сумма ряда числового – через предел частичной суммы.

При этом ещё раз подчёркиваю, что все события происходят в некотором промежутке сходимости ряда. Ибо если при каких-то значениях «икс» функциональный ряд 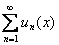расходится, то ни о какой сумме речи быть не может.

Казалось бы, всё просто как пять копеек, однако не тут-то было. Во многих задачах важнА не только сама по себе сходимость, но ещё и её характер суровый, нордический. А сходиться ряд к своей сумме может по-разному: равномерно и неравномерно. Эти термины имеют самый что ни на есть человеческий смысл, в котором мы разберёмся буквально на ближайшем экране. И коль скоро, жизнь довела вас до равномерной сходимости ряда, то объяснять я буду строго – с помощью 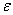-окрестности =) Выкладки будут весьма похожи на определение предела числовой последовательности. Что не удивительно – ведь сейчас мы тоже изучаем последовательность, только функциональную: 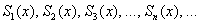– частичных сумм ряда 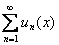в его промежутке сходимости.

Рассмотрим произвольное значение 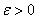, которое может быть сколь угодно малым, и заключим сумму ряда 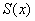в своеобразный «коридор» из двух функци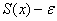й: и 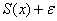. Это и есть 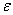-окрестность суммы:

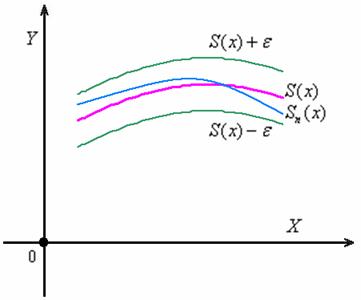
Пусть некоторое приближение 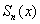(синий цвет) ПОЛНОСТЬЮ лежит внутри «коридора». Аналитически это запишется следующим образом: 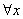(для любого «икс») из промежутка сходимости выполнено неравенство 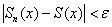. На всякий случай «распакую» модульдля сомневающихся:

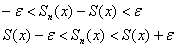
Говорят, что ряд 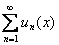сходится равномерно к функции 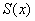на некотором промежутке, если для любого значения 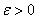(заранее выбранного и сколь угодно малого) и СРАЗУ ДЛЯ ВСЕХ «икс» из данного промежутка найдётся натуральный номер 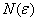(зависящий от «эпсилон»), ТАКОЙ, что для всех номеров 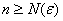будет выполнено неравенство .

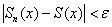Иными словами, равномерная сходимость подразумевает тот факт, что какой бы мизерный«коридор» мы ни рассмотрели – всегда найдётся частичная сумма 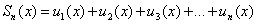, график которой ПОЛНОСТЬЮ окажется внутри «коридора», т.е. будет отличаться от точной суммы по модулю меньше, чем на «эпсилон»:
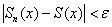– для ВСЕХ «икс» из промежутка сходимости.
И, разумеется, внутри 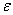-окрестности также окажутся все приближения 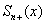более высоких порядков

Изложенное свойство выглядит совершенно естественным, но впечатление это обманчиво. Функциональный ряд может сходиться к своей сумме и неравномерно. В этом случае найдётся такое значение 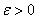(нередко достаточно большое), для которого не существует приближения 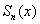, которое бы ЦЕЛИКОМ лежало в коридоре. И здесь типично появление «волны»:

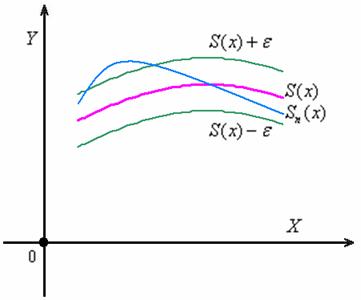
С неограниченным увеличением 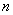график «синего» приближения 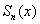будет бесконечно близко приближаться к своей сумме 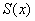, однако ж «волна» никуда не денется – она будет перемещаться справа налево (например) и бесконечно истончаться, но так и останется ВЫШЕ графика «моря» .

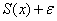Собственно, в этом и проявляется неравномерность сходимости – даже при ОЧЕНЬ больших значениях «эн» график 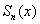уж практически везде сольётся с графиком 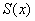, да всё-таки не везде – найдётся малюсенький участок промежутка сходимости, где расхождение 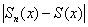будет больше, чем «эпсилон».

Следует отметить, что с геометрической точки зрения неравномерность может проявляться не только «волной». Разберём хрестоматийный пример, который встречается практически в любом учебнике – не могу удержаться, поскольку нагляднее пример найти трудно:

Рассмотрим функциональный ряд 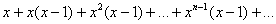и составим последовательность его частичных сумм:

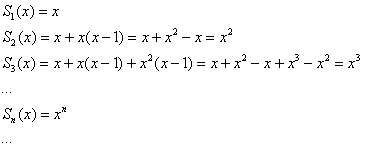
…Эх, где ж мои 12 лет? =) В ходе изучения математики, наверное, многие подметили, что на отрезке 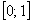с увеличением степени график 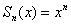всё ближе и ближе прижимается к оси :

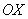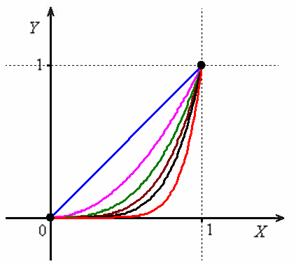
Таким образом, логично предположить, что последовательность частичных сумм 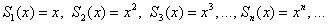сходится к нулевой функции 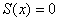на данном промежутке, причём из чертежа явственно виден неравномерный характер этой сходимости – даже при ОЧЕНЬ больших значениях 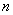найдётся наноскопический участок, где график 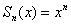окажется «подвешен» к верхней точке, в то время как львиная его часть будет уже «на дне».

Установим факт сходимости аналитически:

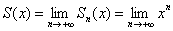
И здесь обнаруживается довольно таки интересная вещь: если 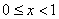, то суммой функционального ряда действительно является ось абсцисс 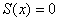, однако при :

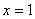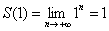
Вот так вот рвутся шаблоны! – несмотря на то, что все члены последовательности 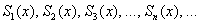непрерывны, её предел терпит разрыв:

И такая ситуация возможна только при НЕравномерной сходимости ряда! Кстати, доказывается неравномерность в данном примере элементарно – берём любую окрестность 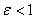и опровергаем определение равномерной сходимости.

Какой можно привести пример равномерно сходящегося ряда? В статье о разложениях функций в степенные ряды в качестве подопытного образца я начал мучить ряд 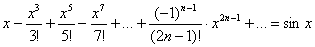и сейчас исследование получает своё продолжение, поскольку сходимость тут как раз равномерна.

Рассмотрим достаточно большой отрезок числовой прямой,… да чего тут мелочиться, пожалуйста, поднимите руку вверх и чуть-чуть согните указательный палец. Это будет начало синусоиды. Теперь мысленно продолжите её до Солнца. …ну, может кто-то хочет до Луны или до соседнего дома – без проблем =) …Представили? Отлично! Обозначим данный кусок через .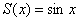

В чём состоит эффект равномерности? Если мы возьмём сколь угодно малую 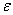-окрестность этого куска, то для неё найдётся натуральный номер 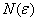(пусть гигантский), начиная с которого: 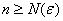, график любого приближения 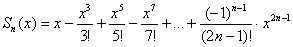ПОЛЬНОСТЬЮ оказывается внутри заявленного «коридора»: 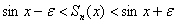– для ВСЕХ «икс» промежутка – что вблизи вашей руки, что вблизи Солнца, что посередине! СТРОГО внутри, никаких «подвисаний» и тем более «заскоков».

И тот же самый факт справедлив для сколь угодно длинного участка синусоиды (т.к. разложение синуса сходится на всей числовой прямой).

Что можно извлечь полезного из этого примера? …Теперь, когда преподаватель заметит ваш необычный жест или застукает в неловкой позе – вам будет, чем оправдаться! =)

А если серьёзно, то равномерность сходимости приносит нам много плюшек, в частности непрерывность суммы ряда (если частичные суммы непрерывны), а также возможность почленно дифференцировать и интегрировать ряд (с некоторыми дополнительными условиями), чем мы уже активно пользовались на уроке о сумме степенного ряда.

Как доказать равномерность сходимости?

Для некоторых рядов это можно сделать с помощью определения. Алгоритм решения опять же похож на доказательство предела числовой последовательности: для произвольной 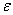-окрестности суммы 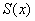нужно указать натуральный номер 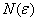– такой, что для любого бОльшего номера 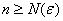и СРАЗУ ДЛЯ ВСЕХ «икс» исследуемого промежутка выполнено неравенство 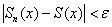. В случае неравномерно сходящегося ряда такого номера не найдётся, поскольку 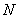будет зависеть ещё и от «икс».

Кроме того, существует эквивалентное определение, сформулированное через остаток ряда. Соответствующие примеры можно найти, например, во 2 томе Бохана, но особенно интересно материал изложен у Фихтенгольца (тоже том 2). Ну а я перехожу практической части урока.

На практике в большинстве случаев определение оказывается малопригодным, и поэтому для выявления равномерности обычно пользуются специальными признаками, которые доказаны в теории. Известнейшим, и, пожалуй, единственным признаком, с которым вам придётся реально столкнуться, называется: