Цели и задачи дисциплины, ее место в учебном процессе, требования к уровню освоения содержания дисциплины

Предисловие

При помощи типовых звеньев можно моделировать различные системы управления и обработки информации. Инженер должен владеть математическими и программными средствами при создании систем управления для автоматизированных систем производства и ремонта вагонов.

В данном методическом указании представлены рекуррентные алгоритмы моделирования типовых звеньев до второго порядка включительно. Целью работы является изучение свойств цифровых алгоритмов и характеристик типовых звеньев.

Цели и задачи дисциплины, ее место в учебном процессе, требования к уровню освоения содержания дисциплины

1.1. Цели и задачи изучения дисциплины

Цель дисциплины – формирование у обучаемых теоретических и практических знаний в области построения систем электроприводов производственных механизмов на предприятиях железнодорожного транспорта с использованием различных электродвигательных устройств и преобразователей, изучение методов расчета и проектирования современных систем электропривода.

Задачи дисциплины: создание у студентов ясного представления о роли и месте электропривода в современной технике и, в частности, в производственных механизмах на предприятиях железнодорожного транспорта; основных задачах, возникающих при разработке современных систем автоматизированного электропривода; принципах построения, расчета и проектирования электроприводов; физических процессах в электроприводах с различными двигателями.

1.2. Требования к уровню подготовки студента, завершившего изучение данной дисциплины

Изучив дисциплину:

- студент должен знать механические характеристики производственных механизмов и электроприводов с различными двигателями; принципы построения и методику проектирования автоматизированных электроприводов; методику выбора приводных двигателей различных производственных механизмов;

- студент должен уметь рассчитывать требуемую мощность двигателя для различных производственных механизмов; выбирать рациональный тип электропривода с учетом заданных требований к его статическим и динамическим свойствам; выполнять расчеты по анализу статических и динамических характеристик электропривода;

- студент должен приобрести навыки расчета мощности электропривода, выбора типа электродвигателя, регулирования основных координат электропривода.

1.3. Краткая характеристика дисциплины, её место в учебном процессе

Основным средством приведения в движение рабочих машин является электрический двигатель и, соответственно, основным типом привода служит электрический привод. Повсеместное использование электропривода в промышленности и железнодорожном транспорте определяет важность изучения этой дисциплины для освоения последующих дисциплин по данной специальности. Вопросы построения и эксплуатации электроприводов различных механизмов в производственных процессах предприятий железнодорожного транспорта являются важными для изучения последующих дисциплин.

Усвоение основных положений курса во многом определяет квалификационную характеристику инженера на железнодорожном транспорте. Востребованность и успешность производственной деятельности инженера базируется на его готовности к квалифицированной эксплуатации электроприводов технологических установок на железнодорожном транспорте.

1.4. Связь с предшествующими дисциплинами

Физика. Вращение твердого тела. Электрический ток. Электромагнетизм.

Теоретические основы электротехники. Анализ переходных процессов классическим и операторным методами.

Электрические машины. Принцип действия, конструкция и характеристики электрических машин.

Теория автоматического управления. Типовые звенья САУ, их передаточные функции. Частотные и переходные характеристики. Устойчивость САУ.

1.5. Связь с последующими дисциплинами

Системы управления электроподвижным составом.

Электрооборудование электроподвижного состава.

Теоретическая часть

Передаточная функция для звена любого порядка имеет вид

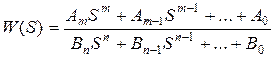, где n>m.

От передаточной функции W(S) необходимо перейти к передаточной функции эквивалентной импульсной системы:

.

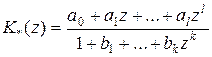По известным коэффициентам A_m, A_m-1,…,A₀ и B_n, B_n-1,…, B₀ можно определить коэффициенты a₀, a₁,…,a_l и b₁,…,b_k. Используя передаточную функцию эквивалентной импульсной системы, находят разностное уравнение (рекуррентный алгоритм) для моделирования линейных динамических звеньев в классе дробно рациональных передаточных функций.

.

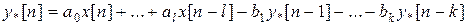Символ * обозначает, то что эквивалентная импульсная система имеет такие же свойства, как и непрерывная система. Начальные условия задаются следующими формулами x[0]=0, x[-1]=0, x[-l]=0, y[0]=0, y[-1]=0, y[-k]=0.

В основу синтеза рекуррентных алгоритмов положен метод z-преобразования. При отсутствии кратных полюсов у передаточной функции системы формула для импульсной переходной характеристики является суперпозицией экспонент:

,

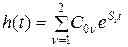где .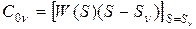

В соответствии с методом z - преобразования передаточная функция эквивалентной импульсной системы определяется соотношением:

,

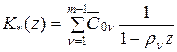где , .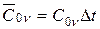

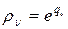В лабораторной работе рассматриваются следующие звенья с передаточными функциями и строятся рекуррентные алгоритмы:

1) Звено первого порядка. Для него имеем:

.

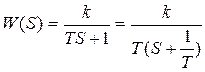Приравнивая знаменатель этого выражения к нулю, находим корень характеристического уравнения:

.

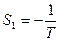Тогда для звена первого порядка получим:

; ,

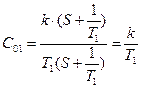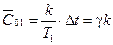где 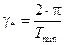тогда .

, , .

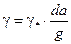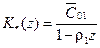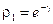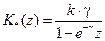С учетом полученных выражений разностное уравнение для звена первого порядка имеет вид

.

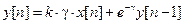Время переходного процесса для звена первого порядка определяется по следующей формуле:

.

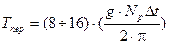2) Звено второго порядка, передаточная функция которого имеет вид

,

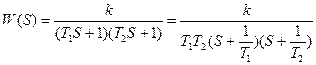корни характеристического уравнения принимают значения: 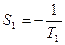, 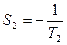. С учетом метода z-преобразования имеем:

;

;

;

;

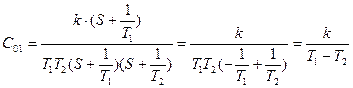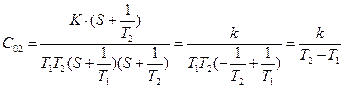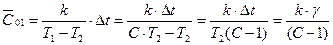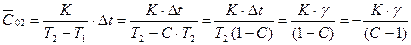где 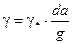- относительное время, .

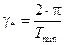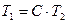, при C>1.

С учетом проведенных преобразований записываем передаточную функцию эквивалентной импульсной системы для звена второго порядка

, ,

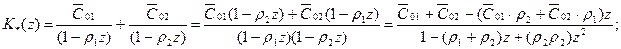
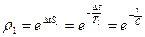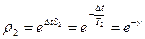по которой определяется разностное уравнение:

.

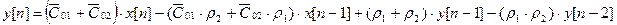Отсюда окончательно получаем:

.

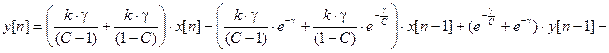
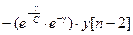В лабораторной работе рассматривается также вариант передаточной функции для звена второго порядка следующего вида:

.

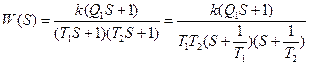Эта передаточная функция описывает важный класс звеньев второго порядка типа четных полосовых фильтров. Для нее корни характеристического уравнения имеют вид

, .

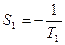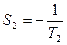Параметры разностных уравнений определяются следующими формулами:

;

;

;

;

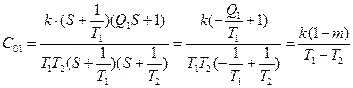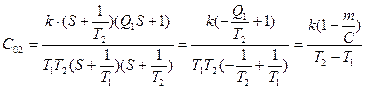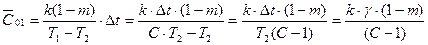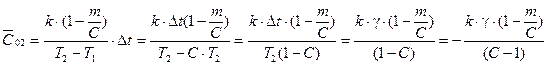где 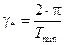тогда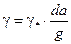

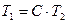, при C>1

.

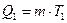С учетом полученных коэффициентов передаточная функция эквивалентной импульсной системы принимает следующий вид:

,

, .

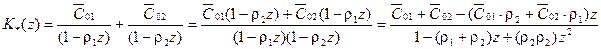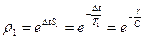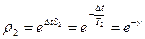От эквивалентной импульсной системы осуществляется переход к разностному уравнению:

.

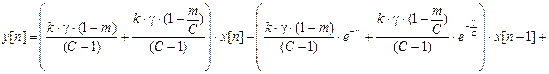
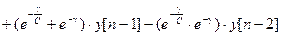Передаточная функция для звена второго порядка может быть представлена еще в одном виде, удобном для физической интерпретации процессов:

,

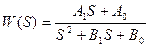где 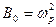[Гц²]. Вводя обозначения, 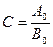, => (следовательно) 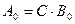, получим:

.

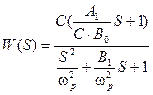Учитывая связь между полосой пропускания (определяемой на уровне 0.707) и добротностью,

,

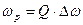где Δω – полоса пропускания, Q – добротность. Окончательно получим:

,

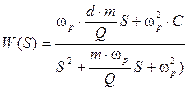где ; .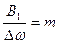

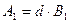Далее определяем импульсно-переходную функцию:

,

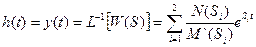где N(S) и M(S) соответственно полиномы числителя и знаменателя W(S), M`(S) производная по S

Отсюда имеем:

.

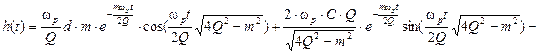
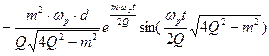Для четного полосового фильтра с ростом Q вклад синусоидальных компонент уменьшается.

Условие нормировки для четного полосового фильтра определяется следующими соотношениями:

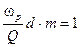[рад/сек] 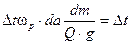[рад]

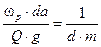[ рад/сек] 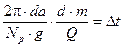[рад]

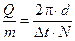[рад]; ,

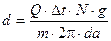где ω_р×Dt=2×p/N, Dt – шаг дискретизации по времени.

da – коэффициент прорежения; g – коэффициент запаса.

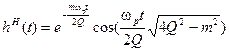[1/сек].

По степени экспоненты 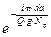определяется время переходного процесса как в четном, так и нечетном фильтрах. Отсюда имеем:

.

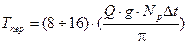Время переходного процесса полосового фильтра определяется с инженерной точностью.

Условие нормировки для нечетного полосового фильтра определяется следующими соотношениями

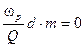, отсюда d=0.

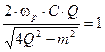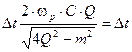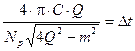, , отсюда .

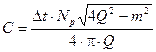С учетом коэффициентов запаса и прорежения имеем ,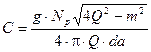

.

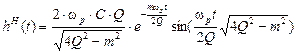С условием нормировки формула для передаточной функции четного полосового фильтра принимает вид

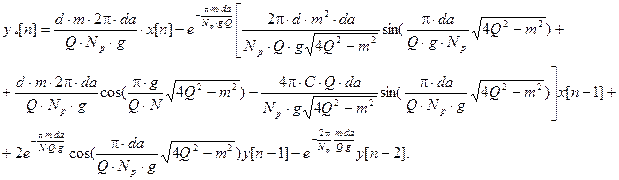
С условием нормировки формула для передаточной функции нечетного полосового фильтра принимает вид