Общие понятия линейной регрессии
Среди методов математико-статистического инструментария эконометрии центральное место занимает регрессионный анализ.
Под регрессией понимают одностороннюю стохастическую зависимость одной случайно переменной от другой или нескольких случайных переменных. В этом смысле регрессия используется для исследования и оценки зависимостей между экономическими явлениями, порожденными, как правило, совокупным действием комплекса причин. Рассматривая причинно-следственные связи, мы хотим из смешанного сочетания причин выявить действие существенных, освободившись от элементов случайности, и действия второстепенных причин. Математическое решение сводится к получению функции регрессии. С помощью методов математической статистики можно исследовать зависимость между такими экономическими показателями как, например, национальный доход, капитальные вложения и трудовые ресурсы. Явления, подлежащие исследованию, должны быть количественно варьирующими величинами. Тогда они считаются переменными в статистическом смысле.
Прежде, чем применять математико-статистический аппарат, явление следует проанализировать с содержательной точки зрения и решить, какую переменную рассматривать как зависимую (следствие), или переменную, подлежащую объяснению с помощью функции регрессии, и какие переменные в ходе анализа считать объясняющими (причины), независимыми, или предсказывающими. Причины и следствия должны быть объяснены экономической теорией.
Далее будем обозначать зависимую переменную через Y, а объясняющие переменные через Xj (j = 1,2,…,p). Переменная Y, таким образом, является функцией от переменных Xj. Задача измерения связи решается на эмпирическом материале, содержащем случайности и влияние второстепенных причин, которые своей изменчивостью затушевывают и искажают интересующую нас зависимость. Поскольку случайности и второстепенные факторы не могут быть исключены из опытных данных, зависимость приобретает стохастический характер, за которым может быть скрыта функциональная (однозначная) связь. С помощью функции регрессии
(2.1)
количественно оценивается усредненная зависимость между исследуемыми переменными. Понятие регрессии всегда связано с определенными средними условиями. Наблюдая за интересующей его зависимостью при сложном взаимодействии факторов-причин и случайностей, исследователь, с помощью регрессии, отвечает на вопрос: какова была бы зависимость между следствием и выделенными существенными причинами, если бы прочие факторы не изменялись и тем самым не осложняли и не затушевывали основную зависимость?
Случайная переменная e
(2.2)
характеризует отклонение переменной Y от усредненной величины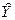 
, вычисленной по функции регрессии (2.1). Случайная переменная e называется возмущающей или, кратко, возмущением. Она включает влияние неучтенных факторов-переменных, случайных помех и ошибок наблюдения. Ее трудно исследовать, поскольку она меняется для каждого наблюдения Y. Если бы мы изучали зависимость национального дохода от капитальных вложений, то случайная возмущающая переменная содержала бы в себе влияние на национальный доход таких факторов, как численность работников в сфере производства, производительность труда, использование основных фондов и т. д., а также различные случайные помехи.
Таким образом, переменную Y можно представить в виде:
, (2.3)
или, с учетом (2.1)
+ e. (2.4)
Этот вид записи позволяет интерпретировать возмущение e как переменную, учитывающую неправильную спецификацию функции регрессии, т.е. неправильный выбор формы уравнения, описывающего зависимость.
Благодаря введению случайной переменной e переменная Y также становится случайной, поскольку при заданных значениях объясняющих переменных 
переменной Y нельзя приписать или поставить в соответствие только одно определенное значение. Если, например, мы изучаем зависимость себестоимости от объема продукции, то, задаваясь значением объема продукции, можно указать диапазон, в котором могут находиться соответствующие значения себестоимости.
Статистические зависимости могут быть обнаружены лишь при многократном повторении наблюдений. Поэтому в дальнейшем мы будем исходить из того, что для (р + 1) переменных имеется n совместных наблюдений ( например, n предприятий). Результаты наблюдений можно представить в виде следующей таблицы:
Таблица 1
| Номер наблюдения | Переменные | |||||
| Y | Х1 | . . . | Хj | . . . | Хр | |
| Y1 | Х11 | . . . | Х1j | . . . | Х1p | |
| Y2 | Х21 | . . . | Х2j | . . . | Х2p | |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| i | Yi | Хi1 | . . . | Хij | . . . | Хip |
| . . . | . . . | . . . | . . . | . . . | . . . | |
| n | Yn | Хn1 | . . . | Хnj | . . . | Хnp |
Каждый столбец таблицы (1) представляет ряд наблюдений над одной переменной, например, введенных в действие основных фондов или объемы производства на n предприятиях. Индекс столбцов j = 1,2,…,p указывает на соответствующую объясняющую переменную, а индекс строки i = 1,2,…,n – на порядковый номер совместных наблюдений над (р + 1) переменными. Таким образом, Xij – результат i-го наблюдения над j-й переменной. Значения Yi и Xij являются эмпирическими (опытными) данными, полученными в результате наблюдений над переменными Y и Xj. Желательно погрешности измерения, а также ошибки наблюдателя-регистратора свести к минимуму, так как зависимость между исследуемыми переменными может искажаться в силу ошибок наблюдений над значениями переменных.
В то время как исследователь располагает значениями зависимой и объясняющих переменных в результате совместных наблюдений над этими переменными, значения возмущающей переменной e непосредственно получить нельзя, поскольку она представляет собой конгломерат многих, трудно учитываемых и случайных влияний. По этой причине e называется также латентной (скрытой) переменной. Лишь после количественной оценки зависимости в виде функции регрессии можно получить количественную характеристику возмущающей переменной e по (2.2). Вычисленные оценки значений возмущения e далее обозначаются е и называются остатками.
Основной задачей регрессионного анализа является спецификация модели, т.е. установление формы связи, подбор такой функции, которая как можно лучше характеризовала бы осредненное массовое течение явления. Избранная функция должна отражать экономическую закономерность. Поэтому на этапе, предшествующем построению регрессии необходим обстоятельный качественный экономический анализ исследуемой зависимости. На основе этого анализа формулируется гипотеза о типе функции, правдоподобие которой затем статистически проверяется по эмпирическим данным.