Тема 7. Функция распределения и плотность распределения вероятностей непрерывной случайной величины

Непрерывная случайная величина может быть задана функцией распределения (называемой также интегральной функцией распределения)

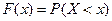или же плотностью распределения вероятностей (называемой также дифференциальной функцией распределения):

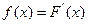(1)

Равенство (1) имеет место в точках непрерывности функции .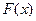

Зная плотность распределения вероятностей, можно найти функцию распределения:

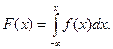(2).

Свойства плотности распределения вероятностей:

1.

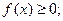
2. 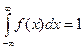. (3)

В частности, если все возможные значения случайной величины принадлежат интервалу (a, b), то

.

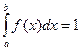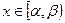Вероятность того, что непрерывная случайная величина примет значение , определяется равенствами:

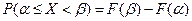
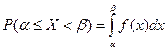. (4).

Задача образец.

Случайная величина задана плотностью распределения вероятностей:

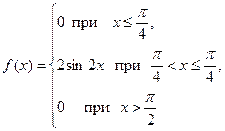
Найти функцию распределения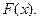

Решение. Если 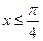, то 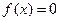, следовательно,

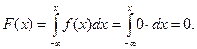
Если 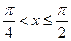, то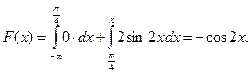

Если 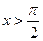, то

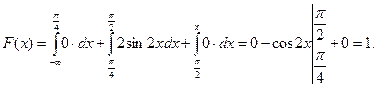
Таким образом, случайная величина имеет следующую функцию распределения:

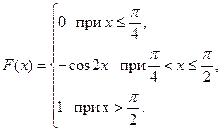
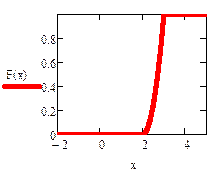
Задача 1.

Случайная величина задана функцией распределения

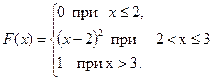
Найти:

а) плотность распределения вероятностей ;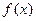

б) графики функци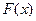й и ;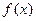

в) по известной функции 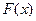и по найденной функции 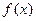найти вероятность того, что в результате испытания примет значения, не меньшее 2,1 и не большее 2,5.

Дать геометрическую интерпретацию величины найденной вероятности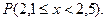

Ответ: а) ;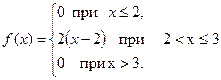

б)

в) 0,24.

Задача 2.

Случайная величина задана функцией распределения

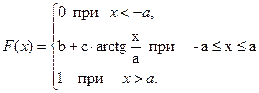
Найти:

а) постоянные b и с.

б) плотность распределения вероятностей величины .

Ответ: а) ;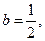

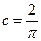б)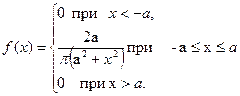

Задача 3.

Случайная величина , все возможные значения которой принадлежат интервалу 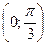, задана в этом интервале плотностью распределения вероятностей 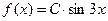. Найти коэффициент .

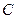Ответ: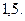

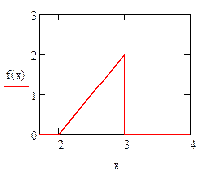
Задача 4.

График плотности распределения вероятностей 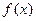случайной величины имеет вид, изображенной на рис. 1.

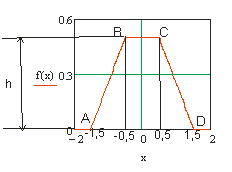
Найти аналитическое выражение для 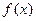на всей числовой оси.

Ответ: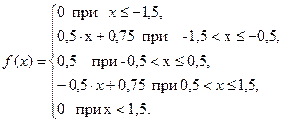

Задача 5.

Случайная величина подчинена закону Симпсона (закону равнобедренного треугольника) на отрезке 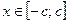рис.2.

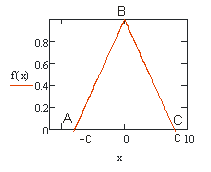
Указание: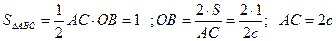

Уравнения прямой 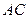и прямой 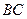найти из уравнения 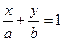, где 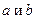отрезки отсекаемые прямой на осях. Получиться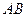 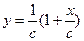для и для .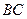

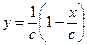Найти:

а) плотность распределения вероятностей этой случайной величины;

б) вероятность попадания величины в интервал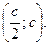

ответ: а)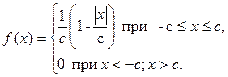

Задача 6.

Дана функция 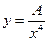. Найти значение постоянного множителя , при котором эта функция могла бы характеризовать плотность распределения вероятностей случайной величины при условии, что все возможные значения величины находятся на луче .

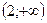Ответ: .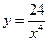

Задача 7.

Дана функция 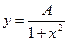. Найти такое значение постоянного множителя , при котором эта функция могла бы охарактеризовать плотность распределения вероятностей случайной величины при условии, что .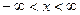

Ответ: .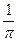

Задача 8.

Случайная величина на всей числовой оси задана дифференциальной функцией распределения 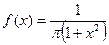(закон Коши).

Найти:

а) функцию распределения случайной величины ;

б) вероятность того, что в результате испытания примет значение из интервала .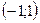

Ответ: а) 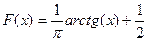; б) 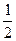.