Взаимное расположение двух прямых на плоскости
Две прямые на плоскости могут
· совпадать;
· быть параллельными;
· пересекаться.
Пусть даны две прямые  и
и  , задаваемые уравнениями
, задаваемые уравнениями  и
и  соответственно. Определим условия, необходимые и достаточные для определения взаимного расположения данных прямых.
соответственно. Определим условия, необходимые и достаточные для определения взаимного расположения данных прямых.
Теорема. Для того чтобы прямые  и
и  совпадали необходимо и достаточно, чтобы
совпадали необходимо и достаточно, чтобы
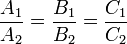 | (7) |
Доказательство. Необходимость. Векторы  и
и  являются направляющими для прямых
являются направляющими для прямых  и
и  , значит, они коллинеарны. Существует такое число
, значит, они коллинеарны. Существует такое число  , что
, что 
Умножим уравнение второй прямой на  и вычтем его из уравнения первой прямой.
и вычтем его из уравнения первой прямой. 
Это равносильно условию (7). Достаточность. Из условия (7) следует, что 
для некоторого  , то есть уравнения, задающие прямые
, то есть уравнения, задающие прямые  и
и  , эквивалентны.
, эквивалентны. 
Теорема. Прямые  и
и  параллельны и не совпадают тогда и только тогда, когда
параллельны и не совпадают тогда и только тогда, когда  (8)
(8)
Доказательство. Необходимость следует из пропорциональности направляющих векторов и справедливости предыдущей теоремы.
Достаточность. Первая часть условия (8) дает параллельность направляющих векторов, вторая — несовпадение прямых. 
Теорема. Прямые  и
и  пересекаются в одной точке тогда и только тогда, когда
пересекаются в одной точке тогда и только тогда, когда  (9)
(9)
Доказательство. Данное утверждение следует из предыдущих двух теорем. Полуплоскости, связанные с данным уравнением
Пусть даны плоскость и лежащая на ней прямая. Две точки 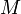 и
и 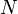 лежат по одну сторону от прямой, если отрезок
лежат по одну сторону от прямой, если отрезок 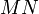 не пересекается с данной прямой. Полуплоскостью называют множество всех точек, которые лежат по одну сторону от прямой.
не пересекается с данной прямой. Полуплоскостью называют множество всех точек, которые лежат по одну сторону от прямой.
Теорема. Если прямая 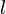 на плоскости задана уравнением (5), то множества
на плоскости задана уравнением (5), то множества 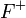 и
и 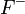 всех точек
всех точек 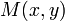 , для которых
, для которых  и
и  , являются полуплоскостями, ограниченными прямой
, являются полуплоскостями, ограниченными прямой 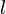 .
.
Доказательство. Пусть точки 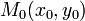 и
и 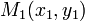 лежат в множестве
лежат в множестве 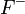 . Рассмотрим произвольную внутреннюю точку
. Рассмотрим произвольную внутреннюю точку 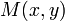 отрезка
отрезка  . Поскольку эта точка делит отрезок в некотором соотношении
. Поскольку эта точка делит отрезок в некотором соотношении  , ее координаты
, ее координаты 
Учитывая очевидное тождество  , получаем
, получаем 
так как обе точки 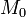 и
и  принадлежат
принадлежат 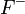 . По определению полуплоскости
. По определению полуплоскости 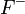 лежит в одной из полуплоскостей, ограниченных прямой
лежит в одной из полуплоскостей, ограниченных прямой 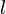 . Аналогичные рассуждения верны и для
. Аналогичные рассуждения верны и для 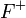 . Поскольку плоскость исчерпывается множествами
. Поскольку плоскость исчерпывается множествами 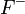 ,
, 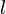 и
и 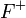 , то множества
, то множества 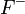 и
и 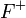 лежат в разных полуплоскостях и исчерпывают их.
лежат в разных полуплоскостях и исчерпывают их. 
Множество 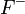 называют отрицательной полуплоскостью по отношению к уравнению (5) прямой
называют отрицательной полуплоскостью по отношению к уравнению (5) прямой 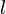 , а
, а 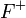 — положительной полуплоскостью.
— положительной полуплоскостью.
Если ту же прямую задать другим уравнением
 | (5') |
то существует такое  , что
, что  . Очевидно, что при
. Очевидно, что при  положительная и отрицательная полуплоскости для уравнения (5') совпадают с такими же для уравнения (5), а при
положительная и отрицательная полуплоскости для уравнения (5') совпадают с такими же для уравнения (5), а при  полуплоскости меняются местами.
полуплоскости меняются местами.
Плоскости в пространстве
Утверждения о плоскости в пространстве аналогичны утверждениям о прямой на плоскости. Основное различие — в размере формул. Поэтому при выводе формул, принципиально не отличающихся от формул для прямой на плоскости, некоторые детали будут опущены.
Уравнения плоскости
Пусть известны координаты точки 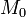 и два неколлинеарных вектора
и два неколлинеарных вектора 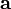 и
и  , лежащих в плоскости. Рассмотрим произвольную точку
, лежащих в плоскости. Рассмотрим произвольную точку 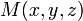 , принадлежащую плоскости. Вектор
, принадлежащую плоскости. Вектор  , очевидно, лежит в плоскости, что по определению означает, что векторы
, очевидно, лежит в плоскости, что по определению означает, что векторы  компланарны. В силу линейной независимости векторов
компланарны. В силу линейной независимости векторов 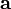 и
и  , это значит, что вектор
, это значит, что вектор  можно линейно выразить через
можно линейно выразить через 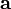 и
и  :
:
 | (10) |
Обозначим через 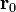 и
и 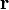 радиусы-векторы точек
радиусы-векторы точек 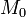 и
и 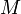 соответственно. Тогда
соответственно. Тогда 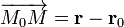 и уравнение принимает вид
и уравнение принимает вид 
Или  (11)
(11)
Уравнение (11) называют векторным уравнением плоскости'.
Возьмем некоторую аффинную систему координат в пространстве. Пусть точки и векторы имеют координаты

Переходя от равенства векторов к равенству их координат, получаем  (12
(12
Это параметрические уравнения плоскости. Эквивалентная система уравнений  выражает линейную зависимость столбцов матрицы
выражает линейную зависимость столбцов матрицы 
что эквивалентно равенству  (13)
(13)
или (после раскрытия определителя по первой строке) уравнению 
Обозначив  , получим общее уравнение плоскости
, получим общее уравнение плоскости  (14)
(14)
Аналогично случаю плоскости можно доказать, что в пространстве плоскости и только плоскости описываются уравнением первой степени.
Если плоскость задана тремя точками с координатами  , не лежащими на одной прямой, то принимают
, не лежащими на одной прямой, то принимают  . Тогда уравнение (13) принимает вид
. Тогда уравнение (13) принимает вид 
