Поверхности второго порядка

Раздел 1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

ТИПОВОЙ РАСЧЕТ № 1

Прямая линия на плоскости.

Кривые второго порядка

Задание 1.

Доказать, что точки А, В, С не лежат на одной прямой.

Задание 2.

Составить уравнения прямых, содержащих стороны треугольника АВС.

Задание 3.

Составить уравнение прямой, проходящей через точку С параллельно стороне АВ.

Задание 4.

Определить взаимное расположение прямой М₁М₂ и прямых, содержащих стороны треугольника ABC.

Задание 5.

Составить уравнение прямой, содержащей медиану АМ.

Задание 6.

Составить уравнение прямой, содержащей высоту СН.

Задание 7.

Определить координаты центра тяжести треугольника ABC (точки пересечения медиан).

Задание 8.

Определить периметр треугольника АВС.

Задание 9.

Определить длину высоты СН.

Задание 10.

Определить площадь треугольника АВС.

Задание 11.

Определить углы треугольника АВС.

Задание 12.

Составить уравнение прямой А’В’, симметричной прямой АВ относительно точки С. Сделать чертеж.

В А Р И А Н Т Ы З А Д А Н И Й 1-12

1.A(–5;2), B(5;7), C(1;–1), M₁(1;2), M₂(5;4).

2.A(–2;10), B(13;5), C(1;1), M₁(5;5), M₂(11;7).

3.A(3;–1), B(–7;–6), C(–3;2), M₁(–3;–1), M₂(–7;–3).

4.A(3;–9), B(–12;–4), C(0;0), M₁(–4;–4), M₂(–10;–6).

5.A(–12;9), B(12;16), C(0;0), M₁(10;–3), M₂(–2;6).

6.A(–7;4), B(3;9), C(–1;1), M₁(–1;4), M₂(3;6).

7.A(–4;10), B(11;5), C(–1;1), M₁(3;5), M₂(9;7).

8.A(–1;–4), B(–11;–9), C(–7;–1), M₁(–7;–4), M₂(–11;–6).

9.A(3;3), B(–12;2), C(0;6), M₁(–4;2), M₂(–10;0).

10.A(–11;8), B(13;15), C(1;–1), M₁(11;–4), M₂(–1;5).

11.A(–4;2), B(6;7), C(2;–1), M₁(2;2), M₂(6;4).

12.A(–2;8), B(13;3), C(1;–1), M₁(5;3), M₂(11;5).

13.A(9;–5), B(–1;–10), C(3;–2), M₁(3;–5), M₂(–1;–7).

14.A(–2;–8), B(–17;–3), C(–5;1), M₁(–9;–3), M₂(–15;–5).

15.A(–13;10), B(11;17), C(–1;1), M₁(9;–2), M₂(–3;7).

16.A(1;8), B(11;13), C(7;5), M₁(7;8), M₂(11;10).

17.A(–1;9), B(14;4), C(2;0), M₁(6;4), M₂(12;6).

18.A(0;–3), B(–10;–8), C(–6;0), M₁(–6;–3), M₂(–10;–5).

19.A(–1;–7), B(–16;–2), C(–4;2), M₁(–8;–2), M₂(–14;–4).

20.A(–10;8), B(14;15), C(2;–1), M₁(12;–4), M₂(0;5).

21.A(–8;6), B(2;11), C(–2;3), M₁(–2;6), M₂(2;8).

22.A(–3;11), B(12;6), C(0;2), M₁(4;6), M₂(10;8).

23.A(6;–7), B(–4;–12), C(0;–4), M₁(0;–7), M₂(–4;–9).

24.A(0;–6), B(–15;–1), C(–3;–3), M₁(–7;–1), M₂(–13;–3).

25.A(–5;14), B(19;21), C(7;5), M₁(17;2), M₂(5;11).

26.A(–6;7), B(4;12), C(0;4), M₁(0;7), M₂(4;9).

27.A(0;6), B(15;1), C(3;–3), M₁(7;1), M₂(13;3).

28.A(8;–6), B(–2;–11), C(2;–3), M₁(2;–6), M₂(–2;–8).

29.A(3;–11), B(–12;–6), C(0;–2), M₁(–4;–6), M₂(–10;–8).

30.A(–14;12), B(10;19), C(–2;3), M₁(8;0), M₂(–4;9).

Задание 13.

Построить указанные кривые второго порядка в прямоугольной декартовой системе координат.

В А Р И А Н Т Ы З А Д А Н И Я 13

1.a) (x–2)² + (y–3)² = 9; 2. a) (x+3)² + (y–5)² = 4;

б) 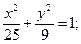б)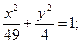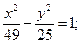

в) в) 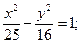г) y² = 9x. г) y² = 7x.

3. a) (x +1)² + (y – 2)² = 16; 4. a) (x–3)² + (y+4)² =25;

б) 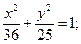б)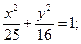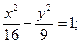

в) в)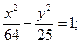

г) y² = 5x. г) y² = 16x.

5. a) (x +3)² + (y +3)² = 4; 6.a) (x–1)²+(y+1)²=1;

б) 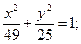б)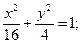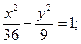

в) в)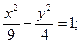

г) y² = 3x. г) y² = 4x.

7.a) (x+2)² + (y–1)² = 36; 8.a) (x–4)²+(y+2)²=49;

б) 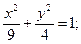б)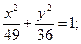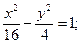

в) в)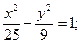

г) y² = 2x. г) y² = 6x.

9.a) (x+4)² + (y–4)² = 9; 10.a) (x–5)²+(y+1)²=4;

б) 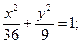б)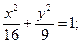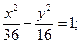

в) в)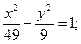

г) y² = x. г) y² = 8x.

11.a) (x+5)² + (y–6 )² = 16; 12.a) (x–1)²+(y+5)²=1;

б) 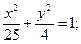б)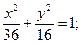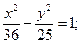

в) в)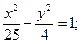

г) y² = –9x. г) y² = –7x.

13.a) (x+1)² + (y–3)² = 25; 14. a) (x–3)²+(y–2)²=36;

б) 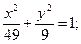б)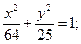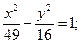

в) в)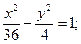

г) y² = –5x. г) y² = –4x.

15.a) (x+2)² + (y+4)² = 49; 16.a) (x–3)²+(y–2)²=9;

б) 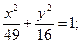б)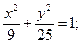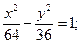

в) в)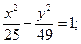

г) y² = –3x. г) y² = –3x.

17.a) (x–5 )² + (y+3)² = 4; 18.a) (x+1)²+(y+1)²=16;

б) 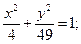б)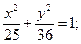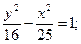

в) в)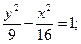

г) y² = –2x. г) y² = –6x.

19.a) (x+4)² + (y–3)² = 25; 20.a) (x–3)²+(y–3)²=4;

б) 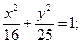б)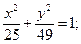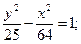

в) в)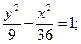

г) y² = –x. г) y² = –8x.

21.a) (x+1)² + (y–1)² = 1; 22.a) (x–1)²+(y+2)²=36;

б) 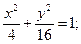б)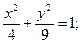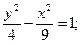

в) в)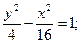

г) x² = 9y. г) x² = 7y

23.a) (x+2)² + (y–4)² = 49; 24.a) (x–4)²+(y+4)²=9;

б) 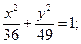б)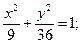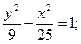

в) в)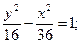

г) x² = 5y. г) x² = 16y.

25.a) (x+1)² + (y–5)² = 4; 26.a) (x–6)²+(y+5)²=16;

б) 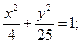б)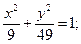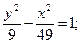

в) в)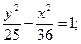

г) x² = 3y. г) x² = 4y.

27.a) (x–3 )² + (y+1)² = 25; 28. a) (x–2)²+(y–3)²=36;

б) 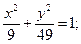б)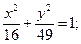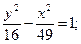

в) в)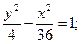

г) x² = 6y. г) x² = y.

29.a) (x+4)² + (y+2)² = 49; 30. a) (x+5)²+(y–1)²=1;

б) 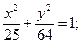б)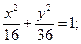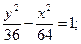

в) в)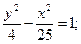

г) x² = 8y. г) x² = 2y.

Задание 14.

Привести уравнение кривой второго порядка к каноническому виду и построить данную кривую в исходной системе координат. Указать формулы перехода от исходной системы координат к канонической.

В А Р И А Н Т Ы З А Д А Н И Я 14

1. 9y² – 4x² +18y –8x–31 = 0.

2.x² + 2y – 4x + 6= 0.

3.4y² + 9x² + 36x = 0.

4. x² + y² + 2x + 4y + 1 = 0.

5.x² –2x – 9y + 1 = 0.

6.x² – 4x – 5 = 0.

7.y² + 6y + 9 = 0.

8.4y² – 25x² + 8y – 96 = 0.

9.y² +4x² – 2y – 8x + 1 = 0.

10.y² + 2y – 3 = 0.

11.x² – 10x + 25 = 0.

12. x² + 2x – 3y + 7 = 0.

13.9x² – 4y² – 36x + 16y–16 = 0.

14. x² + y² – 4x – 2y – 4 = 0.

15.x² – 8x + 16 = 0.

16.9y² + x² – 2x – 8 = 0.

17.x² – 12x + 20 = 0.

18.x² + y² –8x + 4y + 20 = 0.

19.y² + 8y + 15 = 0.

20.y² – 9x² + 6y + 36x – 27 = 0.

21.x² + y² – 6x – 6y + 17 = 0.

22.y² + 2y – 4x – 10 = 0.

23.y² – 4y + x + 8 = 0.

24.4x² + 9y²+8x+18y–23 = 0.

25.x² – 10x + 25 = 0.

26.4у² – 9х² + 8y –18x – 5 = 0.

27.16x²–25y²+64x–50y–361=0.

28.4y² – x² + 8y –2x + 3 = 0.

29.y² + 6y + x + 9 = 0.

30.x² – y² +8y – 16 = 0.

Задание 15.

Построить данные линии в прямоугольной системе координат и заштриховать ограниченные ими области.

В А Р И А Н Т Ы З А Д А Н И Я 15

1.x² = (y + 1); 5x + 2y – 10 = 0; y = .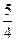

2. 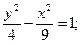2x + 3y – 12 = 0; 2x – 3y + 12 = 0.

3. 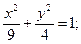x² = y; 2x –3y + 15 = 0.

4. x² = –y; (x – 4)² = –y; y = 0.

5. y = 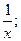x – y = 0; x = 4.

6. (y - 2)² = x; (x –4)² + (у + 4)² = 16; x = 4.

7. 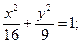x² – y² = 1; x + 5 = 0.

8. (x – 2)² + y² = 4; y² = – (x – 2); x = –2.

9. 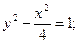x – 3y - 9 = 0; y = –1.

10. y² = – (x – 2); (x – 2)² = y; x – 1 = 0.

11. x² = – (y – 4); 2x – y – 4 = 0; y – 4 = 0.

12. y = – 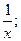x – 2 = 0; 3x + 4y = 12.

13. (y + 2)² = – x; x = 0; y – 1 = 0.

14. x² = – (y – 2); x² = y + 2;y – 4 = 0.

15. (x – 5)² + (y – 2)² = 1; (y – 5)² = (x – 5)²; y = 0.

16.

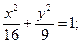
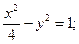
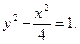
17. y = 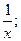x – 5 = 0; y – 4 = 0.

18. (x + 3)² = –(y – 2); 7x + 3y + 21 = 0; x - 3y - 21 = 0.

19. (y – 6)² = x; y² = x; x = 0.

20. (y – 1)² = x + 1; x + 1 = 0; 4x + 3y – 11 = 0.

21. y² = x; (y – 1)² = –(x – 4); x + 2 = 0.

22. 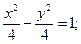(x – 4)² + y² = 1; x – 6 = 0.

23. 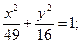(x – 1)² + y² = 1; x = 0.

24. y² = –(x+1); y² = x+3; x – 2 = 0.

25. x² = y; x² + (y–3)² = 1; y – 3,5 = 0.

26. x² + y² = 4; x² + (y–6)² = 4; x² = 4.

27. (x – 2)² = y – 2; (x – 2)² = y + 2; (x – 2)² = 2.

28. y² = x + 4; x – 3y + 6 = 0; x + 3y + 6 = 0.

29. y = – 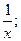x² = y – 3; y – 3 = 0.

30. 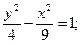x² = 9;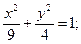

Задание 16.

Построить линию в полярной системе координат.

В А Р И А Н Т Ы З А Д А Н И Я 1 6

1. r = cos²2j. 2. r = 3sin²2j. 3. r = sin4j.

4. r = 3cos3j. 5. r = 1+sin(j+1). 6. r = 2cosj.

7. r = 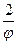. 8. r = 1–2sinj. 9. r = 1–cosj.

10. r = 1+2cosj. 11. r = –4sinj. 12. r = – .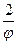

13. r = 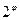. 14. r = 1–sin2j. 15. r =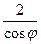

16. r = 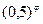. 17. r = 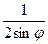. 18. r = – .

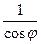19. r = –2j. 20. r = 0,5j. 21. r = .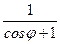

22. r = 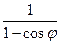. 23. r = 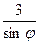. 24. r = .

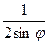25.r = 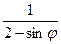. 26.r = 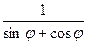. 27.r= .

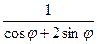28.r= 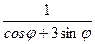.29.r= 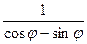.30.r=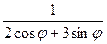

ТИПОВОЙ РАСЧЕТ № 2

Плоскости и прямые в пространстве.

Поверхности второго порядка

Задание 1.

Доказать, что точки А, В, С, D не лежат в одной плоскости.

Задание 2.

Cоставить уравнения плоскостей, содержащих грани пирамиды АВСD.

Задание 3.

Составить уравнение плоскости, проходящей через вершину D пирамиды параллельно грани АВС.

Задание 4.

Составить уравнение плоскости, проходящей через ребро АВ параллельно ребру СD.

Задание 5.

Cоставить уравнение прямой, содержащей ребро СD.

Задание 6.

Составить уравнение прямой, проходящей через точку В параллельно ребру АС.

Задание 7.

Найти объем пирамиды ABCD.

Задание 8.

Найти длину высоты пирамиды ABCD, опущенной из вершины D.

Задание 9.

Найти площадь грани АВС пирамиды ABCD.

Задание 10.

Найти величину двугранного угла при ребре AB.

Задание 11.

Составить уравнение плоскости, проходящей через точку D перпендикулярно ребру АВ.

Задание 12.

Составить уравнение прямой, содержащей высоту DН пирамиды ABCD.

Задание 13

Найти координаты основания H высоты пирамиды ABCD, опущенной из вершины D.