Поверхности второго порядка
Поверхностями второго порядка называются такие множества точек в пространстве, координаты которых удовлетворяют уравнению вида
Ax2+ Вy2 + Cz2 + Dxy + Eyz + Fzx + Gx + Hy + Kz + L = 0. (25)
Например, уравнение
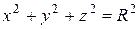
определяет сферу радиуса R с центром в начале координат.
При помощи поворотов и параллельного переноса осей координат всякое уравнение вида (25) может быть преобразовано к каноническому виду. Рассмотрим далее основные канонические уравнения, соответствующие типы поверхностей второго порядка и их наиболее важные свойства.
4.1.
|
|

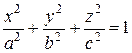 . (26)
. (26)
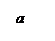
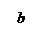
|
| |
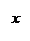
|


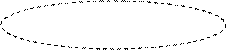 Уравнение (26) называется канони-ческим уравнением эллипсоида. Величины a, b, c - полуоси эллипсоида (рис. 10). Сечением эллипсоида любой плоскостью, параллельной координатным плоскостям, является эллипс (в частном случае окружность).
Уравнение (26) называется канони-ческим уравнением эллипсоида. Величины a, b, c - полуоси эллипсоида (рис. 10). Сечением эллипсоида любой плоскостью, параллельной координатным плоскостям, является эллипс (в частном случае окружность).Координаты точек эллипсоида удовлетворяют неравенствам - a £ x £ a, - b £ y £ b, - c £ z £ c.
В частном случае, при a=b, эллипсоид является поверхностью вращения, получающейся при вращении вокруг оси Oz эллипса 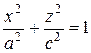 , лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.
, лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.
4. 2. Гиперболоиды.
Гиперболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
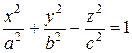 , (27)
, (27)
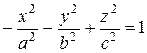 . (28)
. (28)
 | |||
 | |||
|
|
|
 |  | ||||
 | |||||
|
| |
|
|
|
|
Рис. 11 Рис. 12
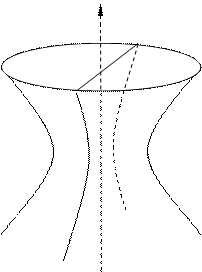
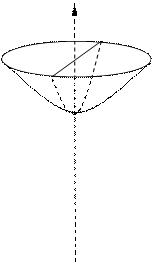
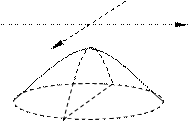
Гиперболоид, определяемый уравнением (27), называется однополостным (рис. 11); гиперболоид, определяемый уравнением (28), называется двуполостным (рис. 12). Для обоих видов гиперболоидов сечения, параллельные оси Oz - гиперболы (для однополостного гиперболоида в сечении может быть пара пересекающихся прямых); сечения, параллельные плоскости xOy - эллипсы.
Величины a, b, с называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (27), только первые из них (a и b) показаны на рис. 11. В случае двуполостного гиперболоида, заданного уравнением (28), одна из них (именно с) показана на рис. 12.
Замечание. При a=b гиперболоиды являются поверхностями вращения.
4.3. Параболоиды.
Параболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
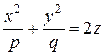 , (29)
, (29)
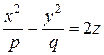 , (30)
, (30)
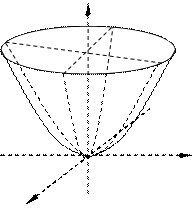
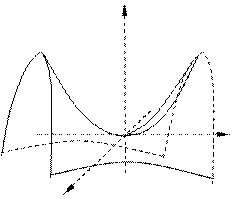
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (29), называется эллиптическим (рис. 13). Сечения эллиптического параболоида, параллельные оси Oz - параболы; сечения, параллельные плоскости xOy - эллипсы. Параболоид, определяемый уравнением (30), называется гиперболическим (рис. 14). Сечения гиперболического параболоида, параллельные плоскостям yOz и xOz - параболы; сечения, параллельные плоскости xOy - гиперболы.
Замечание. В случае, когда p = q, эллиптический параболоид (29) является поверхностью вращения (вокруг оси Oz).
 | |||
 | |||
| |
|
|
| |
|
Рис. 13 Рис. 14
|
|
 Конус, определяемый уравнением
Конус, определяемый уравнением 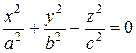 , имеет вершину в начале координат (рис. 15).
, имеет вершину в начале координат (рис. 15). 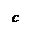
|
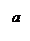
|
|
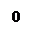





 Поверхность конуса состоит из прямолинейных образующих, проходящих через его вершину и через точки эллипса с полуосями a и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат.
Поверхность конуса состоит из прямолинейных образующих, проходящих через его вершину и через точки эллипса с полуосями a и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат.
|


4.5.Цилиндры.
Поверхности цилиндров состоят из прямых линий (образующих), параллельных оси Oz. Сечениями (перпендикулярными оси Oz) эллипти-ческого цилиндра (его уравнение 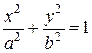 ), гиперболического цилиндра (его уравнение
), гиперболического цилиндра (его уравнение 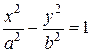 ) и параболического цилиндра (его уравнение
) и параболического цилиндра (его уравнение 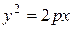 ) соответственно являются эллипсы, гиперболы и параболы.
) соответственно являются эллипсы, гиперболы и параболы.
Пример 20. Определить вид поверхности
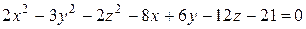 ,
,
используя метод сечения плоскостями.
Решение. Уравнение поверхности не содержит членов с произведением координат, следовательно плоскости симметрий параллельны координатным плоскостям.
Пересекая поверхность плоскостями 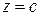 параллельными плоскости xOy, получим:
параллельными плоскости xOy, получим:
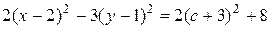 .
.
Так как 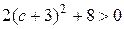 для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
Пересекая поверхность плоскостями 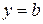 аналогично получаем уравнение
аналогично получаем уравнение
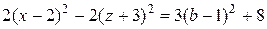
гиперболы с действительной осью, параллельной оси Ox.
При пересечении данной поверхности плоскостями 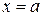 , параллельными координатной плоскости yOz, получаем:
, параллельными координатной плоскости yOz, получаем:
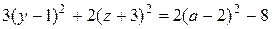 .
.
Последнее уравнение при 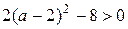 ,т.е. при
,т.е. при 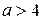 и
и 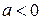 , есть уравнение эллипса.
, есть уравнение эллипса.
Таким образом сечениями поверхности плоскостями являются эллипсы и гиперболы, действительные оси которых параллельны. Следовательно, исследуемая поверхность - двуполостный гиперболоид. Его уравнение можно преобразовать к каноническому виду:
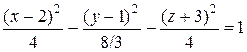 .
.
Понятие множества
При изложении теории множеств мы будем придерживаться так называемой интуитивной точки зрения, согласно которой такие понятия, как "множество", "элемент множества", относятся к начальным понятиям математики и поэтому не подлежат определению.
С понятием множества мы соприкасаемся, прежде всего тогда, когда по какой-либо причине объединяем по некоторому признаку в одну группу какие-то объекты и далее рассматриваем эту группу или совокупность как единое целое.
Множества принято обозначать заглавными латинскими буквами. Объекты, которые образуют множество, называют элементами множества и для обозначения элементов используют, как правило, малые буквы латинского алфавита. Если a является элементом множества M, то будем говорить, что a принадлежит множеству M, и использовать запись a Î M, в противном случае, если a не принадлежит множеству M, будем использовать обозначение a Ï M.
В различных приложениях дискретной математики чаще всего встречаются конечные множества. Интуитивный смысл этого термина ясен: такие множества содержат конечное число элементов. Число элементов конечного множества A называют мощностью этого множества и обозначают символом Card A или |A|. Наряду с конечными множествами в математике рассматривают и бесконечные множества, то есть такие, которые содержат бесконечно много элементов. Так, например, бесконечно множество натуральных чисел N, множество рациональных чисел Q, множество действительных чисел R.
