Сложение матриц. Умножение матрицы на действительное (комплексное) число

Рассмотрим множество M_mn всех матриц размерности m´n с действительными (комплексными) элементами.

Определение 7. Суммой двух матриц одинаковой размерности называется матрица, каждый элемент которой равен сумме соответствующих элементов данных матриц.

Если а_рк и в_рк – соответствующие элементы матриц А и В соответственно и С = А + В, то с_рк = а_рк + в_рк .

Очевидно, сложение матриц обладает следующими свойствами:

· Сумма любых двух матриц одинаковой размерности определена и однозначна.

· А + В = В + А для любых матриц А и В из M_mn.

· (А + В) + С = А + (В + С) для любых А, В, С из M_mn .

· Матрица, все элементы которой равны нулю, играет роль нуля при сложении и называется нулевой матрицей. Её обозначают О (А + О = А ).

· Если обозначить -А матрицу, все элементы которой противоположны соответствующим элементам матрицы А, то А + (-А) = О, т.е. матрица (-А) противоположна матрице А. Итак, каждая матрица имеет противоположную.

Определение 8. Произведением матрицы А на действительное (или комплексное) число l называется матрица В, все элементы которой равны соответствующим элементам матрицы А, умноженным на l.

Если а_рк – элементматрицы А, то в матрице В элемент в_рк =l×а_рк .

Умножение матрицы на число обладает следующими свойствами:

· Произведение любой матрицы на любое число определено и однозначно.

· 1×А = А для любой матрицы А из M_mn .

· 0×А = О для любой матрицы А из M_mn .

· (l×g)×А = l×(g×А) для любой матрицы А из M_mn и любых чисел l и g.

· (l + g)×А = l×А + g×А для любой матрицы А из M_mn и любых чисел l и g.

· l×(А + В) = l×А + l×В для любых матриц А и В из M_mn и любого числа l.

· Если А - квадратная матрица n-го порядка, то |lА| = lⁿ×|А |.

Простые и двойные суммы

Введём некоторые общематематические понятия и обозначения.

Определение 9. Сумма вида а₁ + а₂ + … +а_n называется простой суммой и обозначается 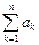. Следовательно, 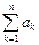= а₁ + а₂ + … +а_n.

Свойства простых сумм:

1⁰. 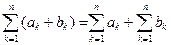, 2⁰. .

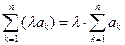Определение 10. Сумма вида

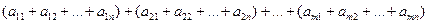называется двойной суммой и обозначается .

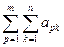Свойства двойных сумм:

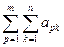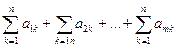1⁰. = ; 2⁰. = .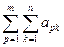

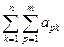Умножение матриц

Пусть А – матрица размерности m´n и В – матрица размерности n´ к. Произведением матрицы А на матрицу Вназывается матрица С, элементы которой получаются следующим образом: каждый элемент р-ой строки матрицы А умножается на соответствующий элемент q-го столбца матрицы В, полученные произведения складываются и результат ставится в пересечение р-ой строки и q-го столбца матрицы С, т.е. с_рq = 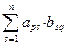(11).

Размерность матрицы С равна m´ к.

Пример 1.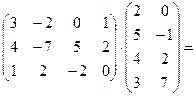

= .

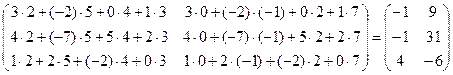Пример 2. Произведение матриц 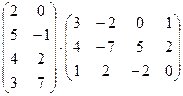не определено.

Но даже если А×В и В×А определены, то они не обязаны быть равны.

Пример 3. А×В = ,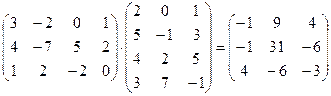

А×В = .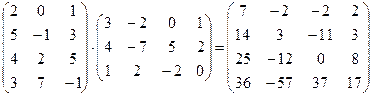

В этом примере А×В и В×А определены, но А×В ¹ В×А . Следовательно, для умножения матриц коммутативный закон не имеет места. Можно проверить:

1⁰. Если (А×В)×С и А×(В×С) определены, то (А×В)×С = А×(В×С).

2⁰. Если (А + В)×С определено, то (А + В)×С = А×С + В×С.

3⁰. Если А×В определено, то (lА)×В =l×(А×В).

3.4. Умножение квадратных матриц одного порядка.

Произведение любых двух квадратных матриц одного порядка всегда определено. При умножении двух квадратных матриц n-го порядка получится матрица того же порядка.

Теорема 7. Определитель произведения квадратных матриц одного порядка равен произведению определителей сомножителей.

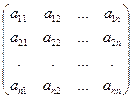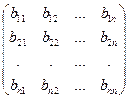Доказательство. Пусть А = , В = . Составим

С =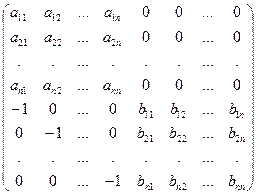

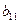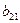матрицу С и вычислим её определитель двумя способами. Сначала используем теорему Лапласа, разложив его по первым n строкам. Получим |С|= |А|×|В|. Для вычисления вторым способом преобразуем матрицу С, используя те преобразования, которые не меняют определитель. К (n +1)-му столбцу матрицы С прибавим 1-ый столбец, умноженный на , 2-ой столбец, умноженный на , … , n-ый столбец, умноженный на .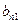

Тогда в (n +1)-м столбце напервых n местах будут стоять элементы первого столбца матрицы А×В, а на остальных местах – нули.

С1 =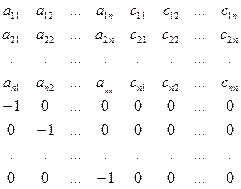

Продолжая аналогичные преобразования с (n +2)-м и т.д. столбцами, получим матрицу С1. Здесь скр – элементы произведения А×В. Очевидно, |С1| = |С|. Определитель матрицы С1 вычислим, разлагая его (по теореме Лапласа) по последним n строкам. Получим |С| = (-1)n×(-1)к×|А×В|, где к = 1 + 2 + …+ n + + (n + 1) + … + 2n = (2n + 1 )×n. Так как (2n + 1 )×n + + n = 2(n + 1 ), то |С| = |АВ |. Итак, |АВ | = |А|×|В| (12).

Если |А| ¹ 0, то матрица А называется невырожденной, если же |А| = 0, то матрица А вырожденная. Из теоремы 7 следует, что произведение двух невырожденных квадратных матриц одного порядка есть невырожденная матрица того же порядка, если же одна из матриц вырожденная, то их произведение – тоже вырожденная матрица.

Квадратная матрица Е = 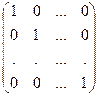называется единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, |Е| = 1.

Определение 11. Матрица В называется правойобратной для матрицы А, если В×А= Е и левой обратной для А, если А×В = Е.

Возникает вопрос, всякая ли квадратная матрица имеет левую или правую обратную матрицу. Если В – левая или правая обратная матрица, то (по теореме 7) |В|×|А| = |А|×|В| = 1, т.е. матрица А не может быть вырожденной.

Пусть А квадратная невырожденная матрица, найдём алгебраические дополнения для всех её элементов. Составим новую матрицу А^* следующим образом: алгебраические дополнения элементов к-ой строки матрицы А поставим в к-ый столбец матрицы А^*, т.е. А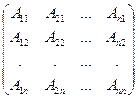^* = . Матрица А^* называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что

А×А^*= А^*×А = 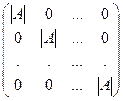= |А|×Е.

Так как |А| ¹ 0, то матрица В = 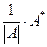существует и А×В = В×А = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А^-1. Итак, получили

Теорема 8. Для всякой квадратной невырожденной матрицы существует обратная матрица. Обратная матрица перестановочна с данной матрицей и вычисляется по формуле

А^-1= 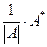(13)

Пример 4. Найдите обратную матрицу, если А = .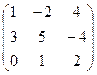

Решение. Найдём |А| = 10 + 12 + 0 – 0 + 4 + 12 = 36.

Составим присоединённую матрицу, для этого вычислим алгебраические дополнения. А₁₁ = 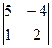= 14, А₁₂ = 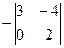= - 6, А₁₃ = 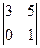= 3, А₂₁ = 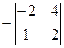= 8, А₂₂ = 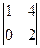= 2, А₂₃ = 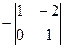= -1, А₃₁ = 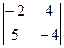= 28, А₃₂ = 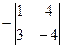= 16, А₃₃ = 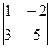= 11. Используя теорему 8, получим А^-1 = .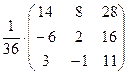