Пример 1

Атом массой m с гамильтонианом и энергией e находится в трехмерном изолированном объеме V, где все точки и направления равноправны. Найти макрохарактеристики фазового ансамбля. Рассмотреть газ из N атомов.

Система изолирована, тогда ,

.

Фазовый ансамбль состояний находится в импульсном пространстве на трехмерной сфере радиусом

.

Микросостояния отличаются направлениями вектора импульса и положениями в объеме V. Число микросостояний внутри гиперповерхность находим из (2.2б)

.

При , 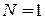получаем

.

Используем

,

находим число микросостояний

. (П.2.4)

Одночастичная энергетическая плотность состояний (2.22)

равна

. (П.2.5)

Плотность состояний классической частицы пропорциональна объему V, доступному для частицы, и корню квадратному из энергии.

Из (2.68)

и (П.2.4), (П.2.5) находим тепловую энергию

. (П.2.6)

Следовательно, средняя энергия частицы, пропорциональная тепловой энергии

.

При нормальной температуре

.

Из (2.64), (П.2.5)

,

,

и (П.2.4)

,

находим давление, создаваемой фазовым ансамблем, соответствующим одной частице:

,

где учтено (П.2.6) . Получено уравнение идеального газа из одной частицы .

Энтропию находим из (2.71) и (П.2.4)

,

получаем

,

где . Энтропия понижается при уменьшении объема сосуда и энергии частицы.

Частный случай – азот N₂. Масса атома

.

При

, ,

получаем

,

.

На интервале энергии находятся уровней, следовательно, классический газ имеет квазинепрерывный спектр.

Для N одинаковых частиц идеального газа полная энергия складывается из энергий отдельных частиц

,

где – проекция импульса одной из частиц на декартову ось. Получаем уравнение сферы в 3N-мерном импульсном пространстве радиусом . Объема шара вычисляем по формуле (П.2.1)

, .

Получаем

,

,

тогда

,

.

Из (2.68) 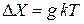находим

– температура пропорциональна средней энергии частицы.

Давление

.

Получено уравнение идеального газа .