Геометричний зміст визначеного інтеграла полягає у тому , що визначений інтеграл дорівнює площі криволінійної трапеції.

Площа криволінійної трапеції обчислюється за формулою:

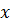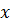Якщо площі тоді для знаходження можна скористатися формулою:

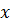Якщо фігура обмежена графіками неперервних функції таких, що для будь-якого , де абсциси точок перетину, тоді для знаходження її площі можна скористатися формулою

4) Фізичний зміст інтеграла

Під час прямолінійного руху переміщення чисельно дорівнює де швидкість руху

5) Обчислення об’ємів тіл

Нехай криволінійна трапеція опирається на відрізок осі абсцис та обмежена зверху графіком функції , невід’ємної та неперервної на відрізку .

Унаслідок обертання цієї криволінійної трапеції навколо осі абсцис утворюється тіло , об'єм якого можна знайти за формулою:

Приклад 1. Обчислити за допомогою формули Ньютона Лейбніца інтеграли.

Приклад 2.

Обчислити площу фігури, обмеженої лініями

Розв’язання

На координатній площині зображаємо задані лінії. Графіком функції є парабола, вітки якої направлені вгору.

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAgWe3HMUA AADeAAAADwAAAGRycy9kb3ducmV2LnhtbESPzYrCMBSF94LvEK7gTlOLilSjSEFGRBc6btxdm2tb bG5qk9E6Tz9ZCLM8nD++xao1lXhS40rLCkbDCARxZnXJuYLz92YwA+E8ssbKMil4k4PVsttZYKLt i4/0PPlchBF2CSoovK8TKV1WkEE3tDVx8G62MeiDbHKpG3yFcVPJOIqm0mDJ4aHAmtKCsvvpxyjY pZsDHq+xmf1W6df+tq4f58tEqX6vXc9BeGr9f/jT3moFk+k4DgABJ6CAXP4BAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQCBZ7ccxQAAAN4AAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt">

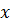s

Відповідь: 9( кв. од.)

Приклад 3.

Обчислити площу фігури, обмеженої лініями та віссю

Розв’язання

1) На координатній площині зображаємо задані лінії . Графіком функції є парабола, вітки якої направлені вгору.

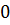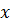2) Знайдемо координати вершини параболи:

3) Знайдемо абсциси точок перетину параболи

Отже, числа 0 та 4 – границі інтегрування.

На відрізку функція від’ємна. Знайдемо площу фігури.

Відповідь: (кв. од.)

Приклад 4.

Обчислити площу фігури, обмеженої лініями

Розв’язання

На координатній площині зображаємо задані лінії:

1)

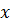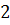Графіком є парабола, вітки якої направлені в гору. Знайдемо координати вершини параболи.

Отже (0;2) – координати вершини

2) Знайдемо абсциси точок перетину параболи з прямою

Отже, числа 1 та 2 – границі інтегрування.

3) Графіком є пряма, що проходить через точки

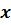		-1

Відповідь: (кв. од.)

Вправи для самостійного розв’язування до теми 12: