Бесконечно большие величины

12.6. Переменная величина 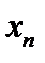называется бесконечно большой, если для любого наперед заданного числа 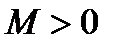можно указать такое натуральное число 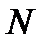, что для всех номеров 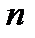, больших 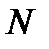, выполняется неравенство 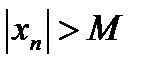. Короче: переменная величина 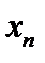называется бесконечно большой, если, начиная с некоторого номера, она становится и остается при всех последующих номерах по абсолютной величина больше любого наперед заданного положительного числа 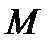. Если 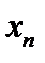есть величина бесконечно большая, то это записывается так: 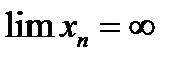, или .

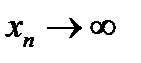Следует определить внимание, что из определения бесконечно большой величины следует, что знак 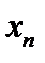роли не играет, а требуется лишь, чтобы абсолютная величина 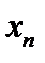, т.е. 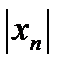, могла быть сделана больше любого наперед заданного положительного числа.

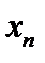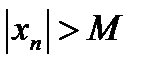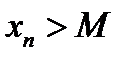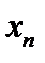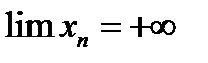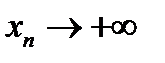Бесконечно большая величина называется положительной бесконечно большой величиной, если, начиная с некоторого номера, она становится положительной. В этом случае уже нет надобности писать , знак абсолютной величины (прямые скобки) можно опустить и писать . В случае, когда - положительная бесконечно большая величина, пишу , или , и произносят: « 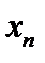стремиться к плюс бесконечности».

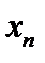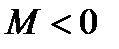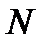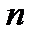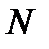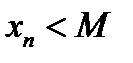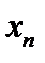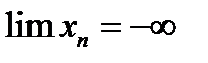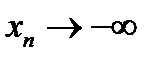12.7.Переменная величина называется отрицательной бесконечно большой величиной, если для любого числа можно указать такое натуральное число , что для всех номеров больших , выполняется неравенство . В случае, когда - отрицательная бесконечно большая величина, пишут , или , и произносят: « 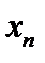стремиться к минус бесконечности».

12.8.Надо понимать, что символы 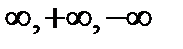отнюдь не являются числами, а вводятся только для упрощения записи и для сокращенного словесного выражения того факта, что переменная величина является бесконечно большой, положительной бесконечно большой и отрицательной бесконечно большой. Следует твердо понимать, что никаких арифметических действий над этими символами производить нельзя.

12.9.Бесконечная большая величина предела не имеет.

12.10.Переменная, принимающая значения, обратное по величине соответственным значениям бесконечно малой величины, есть величина бесконечно большая.

12.11.Переменная, принимающая значения, обратные по величине соответственным значениям бесконечно большой величины, есть величина бесконечно малая (хотя в некоторых учебниках и применяются условия запис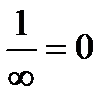и и 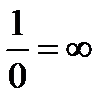, но их следует всячески избегать, так как 1) делить на нуль запрещено, 2) делить же на 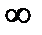тоже нельзя, ибо 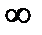не число, а символ, делить же на символ бессмысленно).

12.12. Если 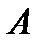постоянная величина, не равная нулю, то произведение 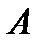на бесконечно большую величину есть величина бесконечно большая.

12.13. Произведение двух бесконечно больших величин есть величина бесконечно большая.

12.14. Отношение бесконечно большой величины к бесконечно малой есть величина бесконечно большая.

12.15. Сумма двух бесконечно больших величин одинакового знака есть бесконечно большая величина такого же знака.