Лекция№9. ТЕРМИЧЕСКОЕ ДЕЙСТВИЕ ТОКОВ В СХЕМАХ ЭНЕРГОУСТАНОВОК.

Тема: Электрические станции и подстанции

9.1 Нагрев токоведущих частей и уравнение теплового баланса

При работе токоведущих частей выделяют продолжительный и кратковременный режимы нагрева. Оборудование электростанций и подстанций в нормальных условиях работает в продолжительном режиме, а при коротких замыканиях в кратковременном режиме нагрева.

Процесс нагрева проводников в этих режимах можно описать с помощью уравнения теплового баланса. Составим это уравнение.

Пусть по длинному проводнику, имеющему сопротивление R, удельную теплоёмкость c, массу m и помещённому во внешнюю среду с температурой θ_ср протекает ток I. Для малого интервала времени dt можно составить уравнение теплового баланса:

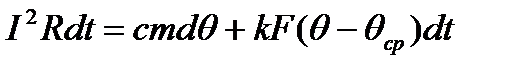. (1)

Здесь левая часть уравнения определяет тепло, которое выделилось в проводнике за время dt, первый член правой части определяет тепло расходованное на повышение температуры проводника на dθ градусов за время dt. Второй член правой части определяет тепло выделившееся в окружающую среду за время dt при условии, что k – коэффициент теплоотдачи, учитывающий все её виды (теплопроводность, конвекция, излучение), F – поверхность проводника, а θ – температура проводника.

Продолжительный режим нагрева – это режим с постоянной нагрузкой в течение неограниченного времени, когда проводник или аппарат находится в установившемся тепловом состоянии, достигая неизменной температуры.

Каждый проводник и изоляционный материал имеют допустимые температуры в продолжительном режиме θ_доп.дл. Например, изоляция в зависимости от класса имеет следующие допустимые температуры:

класс	У	А	Е	В	Р	Н	G
θдоп.дл ,0С							>180

Для неизолированных медных и алюминиевых проводников длительно допустимая температура 70^оС.

Уравнение теплового баланса в продолжительном режиме примет вид:

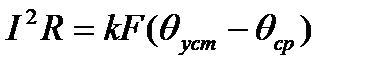. (2), т.к. при некоторой установившейся температуре проводника θ_уст его температура не изменяется и, следовательно, dθ=0. На основании (2) можно получить связь между током в проводнике I в установившемся режиме и его температурой θ_уст:

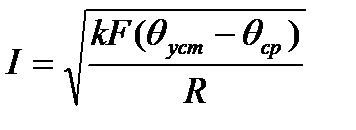.(3)

Номинальным называют длительно допустимый ток проводника, при котором проводник достигает длительно допустимой температуры θ_доп.дл при стандартизированной температуре окружающей среды θ_ср.ст.

Среда	СТАНДАРТИЗИРОВАННАЯ ТЕМПЕРАТУРА θср.ст,оС
Воздух для проводников	+25
Воздух для аппаратов	+35
Земля	+15
Вода	+15

На основании (3) можно получить выражение для I_ном:

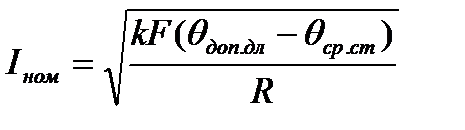. (4)

Если температура окружающей среды не равна стандартной, то говорят о допустимом токе проводника при данных условиях:

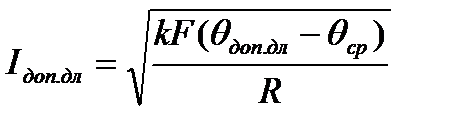. (5)

Если взять отношение допустимо длительного и номинального токов, то можно получить связь между этими токами:

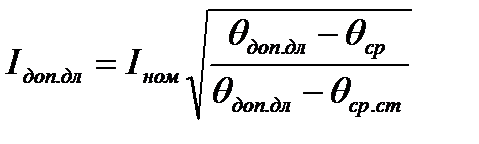. (6)

Из отношения произвольного тока в проводнике I и номинального тока можно определить установившуюся температуру проводника θ_уст при произвольной температуре среды θ_ср, отличной от стандартной:

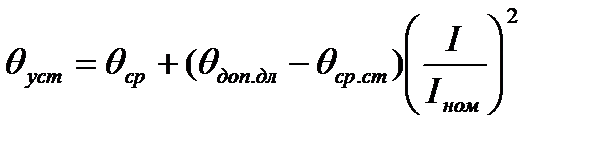. (7)

Нагрев проводников в кратковременном режиме. Критерием термической стойкости проводника в этом режиме является температура его нагрева токами КЗ. Проводники (и аппараты) считаются термически стойкими, если их конечная температура в процессе КЗ не превышает допустимой величины θ_{к доп}.

Определить конечную температуру нагрева проводника θ_к в процессе КЗ можно с помощью уравнения теплового баланса, которое из-за краткости режима КЗ, когда можно пренебречь выделением тепла в окружающую среду, примет вид:

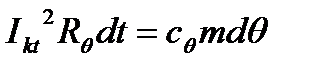. (8)

Здесь I_kt – ток КЗ (действующее значение), который с течением времени t может изменяться;

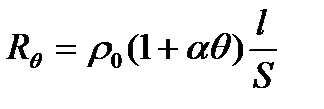- активное сопротивление проводника при текущей температуре θ,

ρ₀ – удельное сопротивление проводника при θ=0⁰С;

l и S – длина и сечение проводника;

α – температурный коэффициент сопротивления;

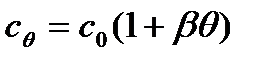- теплоёмкость проводника при температуре θ,

c₀ – теплоёмкость при θ=0⁰,

β – температурный коэффициент теплоёмкости;

m=γlS – масса проводника,

γ – плотность проводника.

Произведем подстановку в уравнение (8) рассмотренных выражений и проинтегрируем по соответствующим переменным:

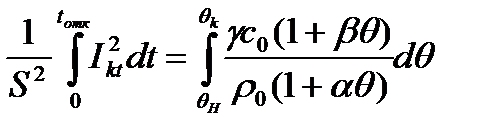. (9)

Здесь t_отк – время с начала КЗ до отключения,

θ_н – начальная температура проводника (перед КЗ),

θ_к – конечная температура проводника (в момент отключения КЗ).

Величина 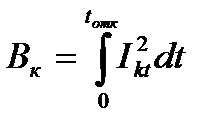пропорциональная количеству тепла, выделенного при КЗ, носит название теплового импульса, а величина 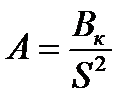носит название удельного теплового импульса. Значение интеграла в правой части соответствующее начальной температуре θ_н обозначим А_н, а конечной θ_k – А_к. Теперь можно записать:

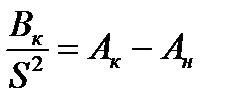или .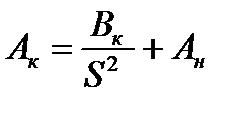

Величина А есть сложная функция температуры проводника и приводится в справочниках в виде графиков для проводников из различных материалов.

Рассмотрим, как с помощью этих графических зависимостей (Рис.9.1) определить конечную температуру проводника.

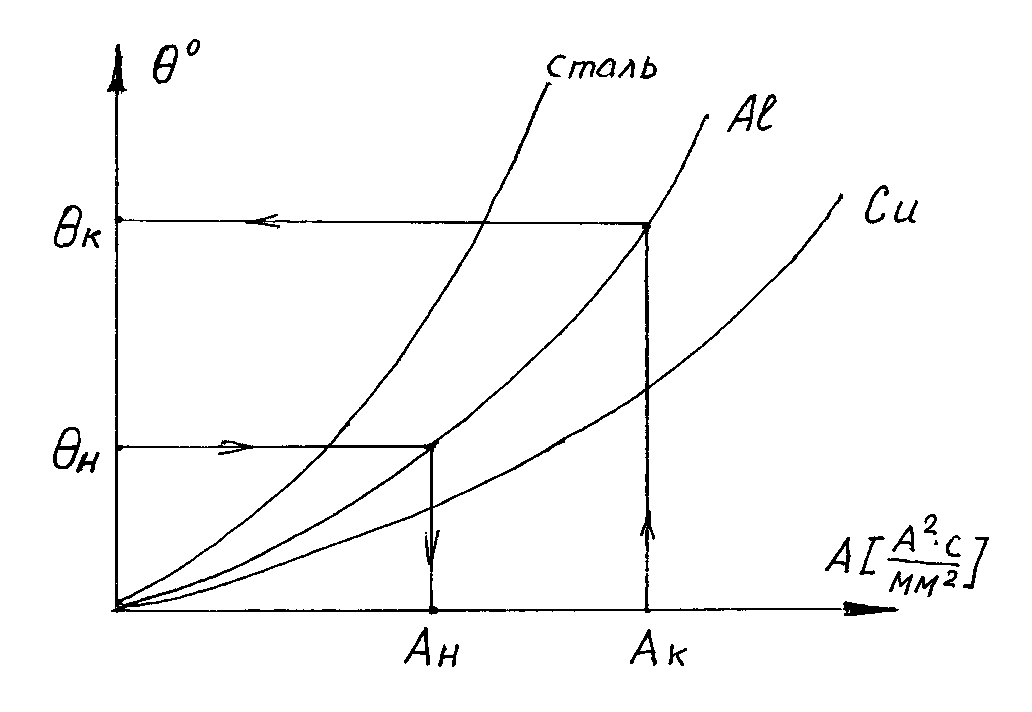
Рис. 9.1 Кривые для определения конечной температуры проводников.

В качестве начальной температуры θ_н принимаемустановившуюся температуру θ_уст проводника перед КЗ, которую вычисляем по ранее приведенной формуле (7), где I максимальный ток нагрузки в проводнике.

Зная θ_н, по кривой A=f(θ) определим А_н. Вычислив В_к, определим 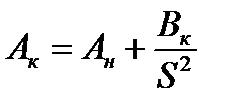, а затем по кривой определим конечную температуру θ_к.Если будет выполняться условие θ_к≤θ_{к доп}, то проводник в данных условиях будет термически стоек.

Таким образом, чтобы с помощью кривых A=f(θ) определить термическую стойкость проводников необходимо уметь вычислять тепловой импульс тока КЗ В_к. Так как ток КЗ в общем случае содержит периодическую и апериодическую составляющие, то и тепловой импульс В_к представляют состоящим из двух составляющих: В_кп – определяется переменной составляющей тока КЗ и В_ка – определяется апериодической составляющей тока КЗ. В_к≈В_{к п}+В_{к а}.

При КЗ недалеко от генераторов (КЗ на выводах генераторов, на сборных шинах распредустройств станций) действующее значение периодической составляющей тока КЗ из-за переходных процессов в генераторах и действия систем возбуждения генераторов изменяется во времени (Рис9.2). Это изменение необходимо учитывать при расчёте теплового импульса от периодической составляющей тока КЗ В_{к п}.

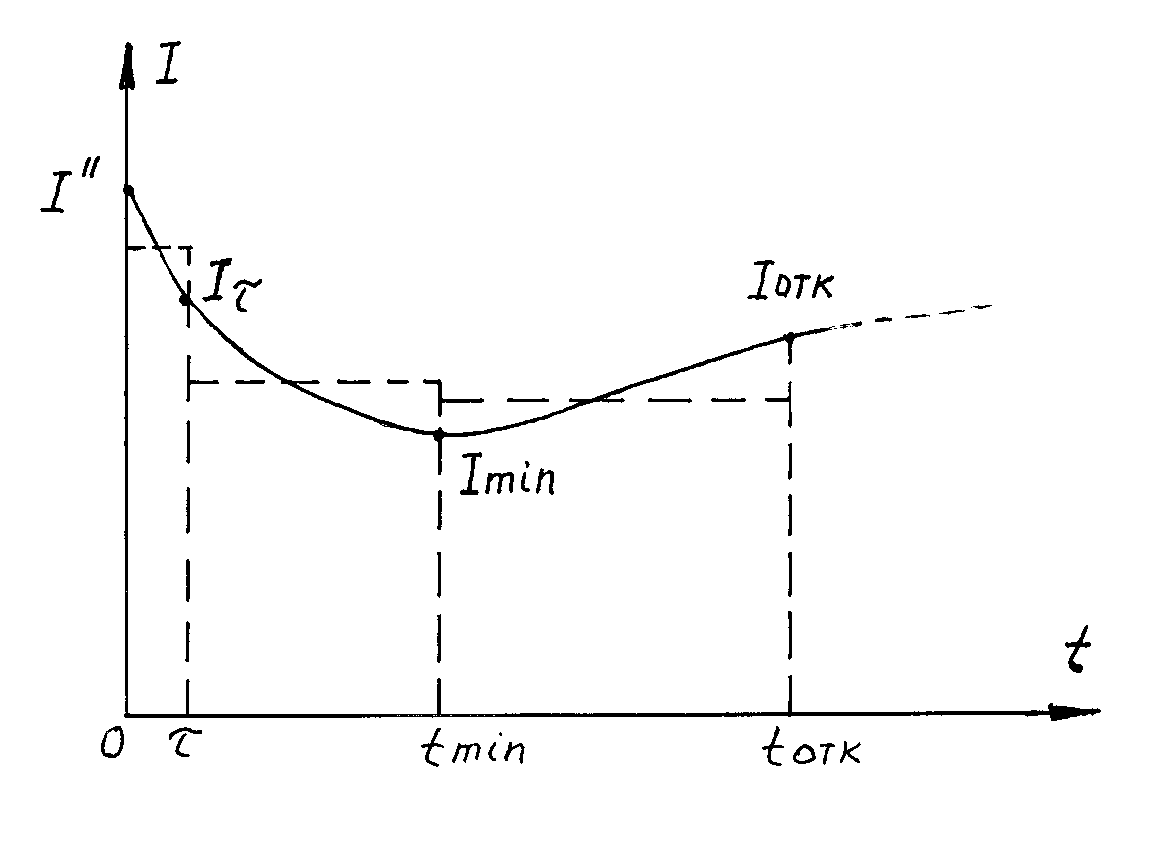
Рис. 9.2 Кривая изменения переменной составляющей тока КЗ для вычисления В_кп.

В расчете В_{к п} участвуют в общем случае следующие токи:

I^’’ – сверхпереходный ток КЗ;

I_τ – периодический ток КЗ в момент начала расхождения контактов выключателя;

I_min – минимальное значение периодического тока КЗ;

I_отк – периодический ток КЗ на момент отключения.

Время начала расхождения контактов выключателя τ=t_св+t_{рз min}, здесь t_св – собственное время выключателя, а t_{рз min} – минимальное время срабатывания основных защит в цепи выключателя (при отсутствии данных принимается 0,01 с).

Время отключения КЗ t_отк=t_во+t_{рз max}, здесь t_во – время отключения выключателя t_{рз max} – максимальное время срабатывания резервных защит в цепи выключателя.

Расчет В_кп основан на аппроксимации площади под кривой I²(t) прямоугольниками. При этом рассматриваются два случая:

1) t_отк>t_min

;

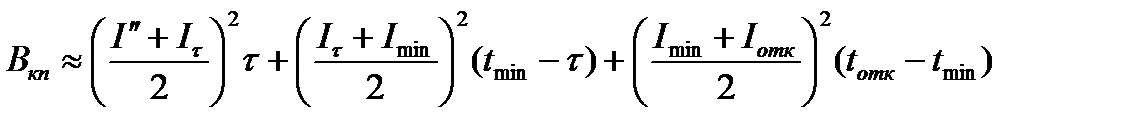2) t_отк<t_min

.

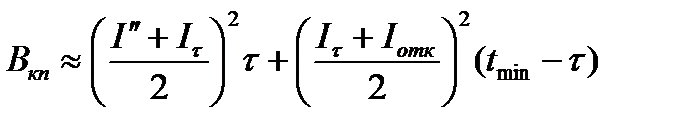При КЗ в распределительной сети, т.е. вдали от генераторов, можно считать, что переменная составляющая тока КЗ не изменяется во время КЗ и равна сверхпереходному току. В этом случае В_кп=I^’’2t_отк.

Апериодическая составляющая тока КЗ, возникнув в первый момент КЗ, затухает по экспоненциальному закону с постоянной времени петли КЗ Т_а. Можно показать, что при t_отк>Т_а тепловой импульс от апериодической составляющей можно принять В_ка≈I^’’2Т_а.

Проверка термической стойкости аппаратов производится не по допустимой температуре, а по допустимому тепловому импульсу. Для этого в справочниках приводится ток термической стойкости I_тер и время его протекания t_тер. По ним можно вычислить допустимый тепловой импульс B_кдоп=I² _тер t_тер. Условием термической стойкости аппарата будет выполнение соотношения В_к≤В_{к доп}.

Аппараты и токоведущие части в цепях генераторов из-за длительного процесса гашения поля генератора при его отключении проверяют при условии, что t_отк=4с.